2

Сооружения и входящие в их состав строительные конструкции в процессе расчёта и проектирования рассматриваются не во всём неисчерпаемом разнообразии свойств и признаков, а с помощью адекватной (обоснованно идеализированной) физической модели, называемой расчётной схемой сооружения ( конструкции ), по которой формируется математическая модель в виде алгоритма, расчётных уравнений и формул.

^*) Согласно [ 9 ], системой (от греческого sýst ēma – целое, составленное из частей; соединение) в технике называется совокупность объектов (элементов) с отношениями и связями между ними, объединённых еди-ной целью и общим алгоритмом функционирования (вариант – предназначенных для исполнения заданной функции).

Предметом строительной механики ( в узком смысле ) как науки и учебной дисциплины являются принципы и методы расчёта сооружений на прочность, жёсткость и устойчивость; а объектом – сооружения ( и их расчётные схемы ), трактуемые как системы^*), функциональной зада-

чей которых является механичес-

кое сопротивление деформирова-

нию заданными воздействиями.

Указанная интерпретация

реального объекта ( сооружения,

к

1

онструкции ) обуславливает то, что в расчёте он представляется расчётной схемой и условно называется системой; при этом термины «расчётная схема системы» и «система» применяются как равносильные.

Под расчётом в строительной механике понимается последовательность действий, результатом которых является получение функциональных описаний или числовых значений величин, характеризующих напряжённо-деформированное состояние сооружения (конструкции), а именно – силовых факторов и переме-щений точек, сечений. Определение напряжений и оценка прочности конструктивных элементов при этом не затрагиваются, так как относятся к предметной области науки о сопротивлении материалов, методы, способы и формулы которой позволяют решать эти вопросы по внутренним силовым факторам, найденным методами строительной механики.

40

Данные методические указания посвящены расчётам особого класса деформируемых систем – статически определимых плоских стержневых систем основных типов ( по общепринятой классификации ) – многопролётных балок, ферм, трёхшарнирных арок и рам ( а также составных систем с трёхшарнирными частями ), комбинированных систем.

Изложение материала в методических указаниях предполагает наличие у читателя знаний основ теории расчёта статически определимых систем разных типов.

Указания составлены в соответствии с программами дисциплин «Строительная механика» для студентов направления 270101 «Строительство уникальных зданий и сооружений» и «Строительная механика и надёжность строительных конструкций» (направление 270800.62 «Строительство», профиль «Промышленное и гражданское строительство») с примерно одинаковыми объемами часов аудиторных (лекционных и практических) учебных занятий (96 и 108 соответственно) и самостоятельной работы студентов (120 и 128 часов). С некоторыми сокращениями в заданиях и объёме, указанными далее в тексте, они могут использоваться также студентами других профилей направления 270800.62 «Строительство» – «Гидротехническое строительство», «Проектирование зданий», «Городское строительство и хозяйство».

Выполнение индивидуальных расчётных заданий по стро-ительной механике способствует

 освоению обучаемыми понятийного аппарата дисциплины, ме-тодов, способов и приёмов расчёта основных типов стержневых систем;

 выработке, на примерах простых систем, навыков оценки «игры сил» ( распределения силовых факторов ) в сооружении или конструкции;

 формированию профессиональных компетенций, предусмотренных образовательными стандартами.

При выполнении задания рекомендуется предварительно изучить теорию соответствующего раздела дисциплины по учеб-никам [ 1 – 3 ], пособиям [ 4, 5 ] и другим, а также разобрать имею-щиеся в них простые примеры. Защите задания предшествует решение обязательного набора характерных задач по теме – в порядке подготовки к этому имеет смысл заранее самостоятельно прорешать несколько типовых задач. Кроме того, для успешной защиты задания следует подготовиться к ответу по теории, используя приведенные далее контрольные вопросы.

Для расширения знаний и навыков в индивидуальные задания включены факультативные дополнения, которые могут выполняться по личной инициативе и желанию обучаемого.

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ РАСЧЁТА

СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ

СТЕРЖНЕВЫХ СИСТЕМ

1.1. Расчётная схема сооружения ( конструкции ),

её кинематический анализ

Подробное изложение представлений о предназначении рас-чётной схемы, требований к ней и правил её формирования содержится в учебниках и пособиях [ 1 – 5 ]. Ввиду того, что реальный объект может быть достаточно сложной системой, образованной из элементов с разнообразными связями между ними, необходимы корректность, чёткость и аккуратность изображения всех компонентов расчётной схемы – элементов (стержней), их соединений (связей) и заданных воздействий. При этом следует придерживаться установленных правил [ 5 ], во избежание разночтений. Нужно видеть различия в узловых соединениях стержней ( рис. 1.1, а ), в опорных узлах ( рис. 1.1, б, в ).

а)

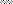
б) в)

Не рекоменд.

Рис. 1.1

19

20

Расчёту рассматриваемой системы должен предшествовать кинематический анализ её расчётной схемы [ 4, 5 ], осуществляемый в два этапа:

W , ( 1.1 )

24

1) количественный анализ – проверка выполнения необходимого, но недостаточного условия геометрической неизменяемости системы

г

22

де W = n_ – n_c = 3D – (3П + 2H + C + C₀) – для плоской системы;

D, П, H, C, C₀ – количества соответственно дисков, припаек,

шарниров, внутренних связей 1-го типа и внешних (опорных)

связей; П и Н – с учётом возможной кратности, C₀ – в пере-

счёте на связи 1-го типа^*) ;

^{* )} Подробнее см. [ 5 ], где даны терминология, истолкование формул,

описание методики и алгоритмов кинематического анализа.

26

30

2) качественный ( структурный ) анализ – в случае выполнения условия ( 1.1 ) – оценка правильности расположения внутренних и внешних связей системы по типовым способам геометрически неизменяемого соединения дисков плоских систем:

 прикрепление к диску точки ( диска бесконечно малых размеров ) двумя линейными связями ( рис. 1.2, а);

 соединение двух дисков тремя линейными связями ( рис. 1.2, б) или с помощью шарнира и линейной связи ( рис. 1.2, в);

 соединение трёх дисков попарно тремя шарнирами ( рис. 1.2, г) или тремя парами линейных связей ( рис. 1.2, д).

Правила корректного размещения связей, а также кинематические и статические характеристики соединений приведены в [ 5 ]. Следует иметь в виду, что в результате правильного наложения связей получается новый диск, и лишь в том случае, когда один из соединяемых дисков – «земля», можно констатировать образование геометрически неизменяемой системы.

A

а) б) в) г) д)

D₂

D₃

D₃

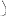
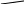
D

D₂

D₁

D₂

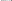
D₁

D₁

D₁

D₂

Р

32

ис. 1.2

^*) Особыми методами, здесь не рассматриваемыми, могут рассчитываться также мгновенно изменяемые и даже изменяемые системы ( механизмы ).

По результатам кинематического анализа расчётной схемы выносится заключение о кинематической природе исследованной системы – является ли она геометрически неизменяемой, изменяемой или мгновенно изменяемой. Расчёту методами строи-тельной механики подлежат,

как правило, геометрически

неизменяемые системы^*).

Если геометрически неизменяемая система имеет характеристику W = 0, то это означает, что она образована с помощью только необходимых связей и не содержит лишних связей. Такая система с точки зрения особенностей работы и расчёта может быть отнесена к классу статически определимых – при условии, что расчёт выполняется без учёта изменения геометрии вследствие деформации элементов ( подробнее об этом – в следующем параграфе ).