2. Схема электрической цепи.

Основные теоретические положения

Векторы активного, реактивного и полного напряжений цепи образуют прямоугольный треугольник, из которого: , или

В этой формуле - общее активное сопротивление, равное арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь; - общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. Здесь индуктивные сопротивления считаются положительными, а емкостные – отрицательными. Полное сопротивление неразветвленной цепи: .

Порядок выполнения работы

1.Изучить теоретический материал.

2.Выполнить задание.

Задание 1. Для схемы рис.1 определить ток и составить баланс мощностей. Известно:

R1 = 3 Oм; R2 = 8 Oм; R3 = 9 Oм; X1L = 4 Oм; X2L = 6 Oм; X1C = 15 Oм; X2C = 10 Oм

Рис.1.

Предварительно выбрав условно положительное направление (фазовый угол сдвига покажет истинное направление э.д.с. и тока), согласно второму закону Кирхгофа уравнение напряжения в векторной форме:

, (1)

или:

Общее активное сопротивление: .

Общее реактивное сопротивление: . (2)

По результату ∑Х можно сделать вывод, что оно носит емкостной характер.

Полное сопротивление цепи

Действующие величины э.д.с.: , .

Суммарная э.д.с. рис.2 (учитывая, что Е1 и Е2 взаимно перпендикулярны) будет .

Ток будет: .

Подсчитаем напряжения на участках схемы, входящие в выражение (1).

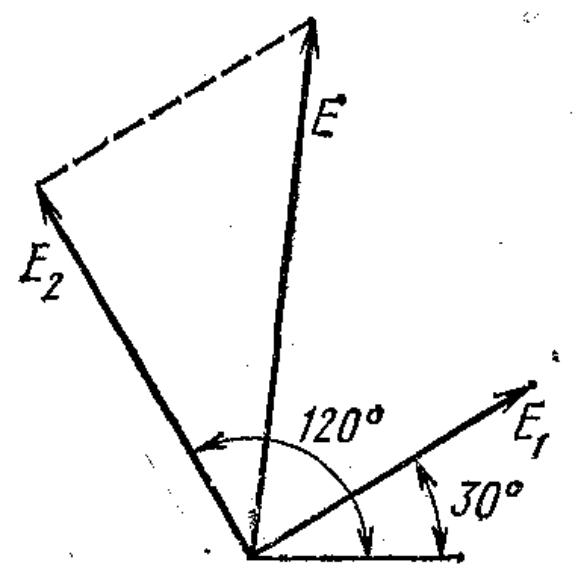Рис.2. Топографическая диаграмма э.д.с.

Исходя из диаграммы рис.2 углы сдвига между током и э.д.с. Е1 и Е2:

Тогда мощности участков приемника: (Вар); (Вт), аналогично для , , , ,

Мощности источников:

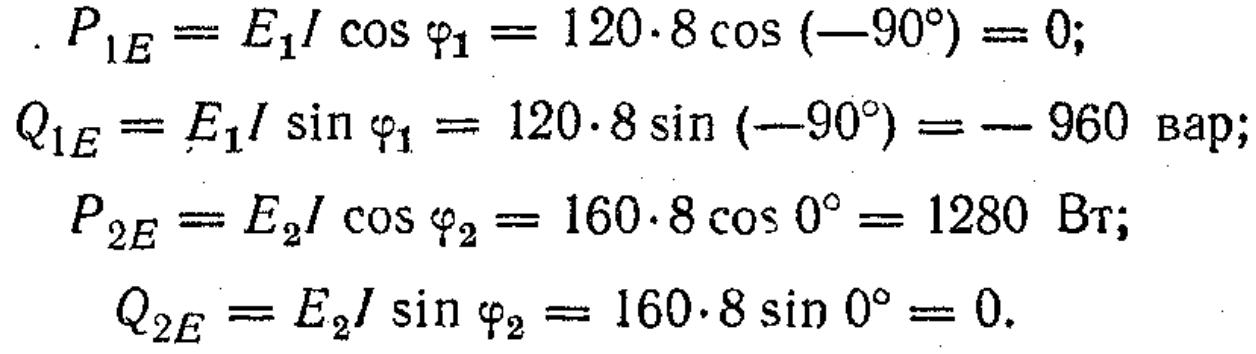
Составим и проверим баланс мощностей нашими расчетами:

и

Контрольные вопросы

1.Как получено выражение (1)?

2.Почему сделан вывод из формулы (2), что ∑Х носит емкостной характер?

3.Откуда можно сделать вывод, что Е1 и Е2 взаимно перпендикулярны?

4.В каких единицах измеряется реактивная мощность?

Лабораторная работа №6 по дисциплине ОП 05. Теория ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Тема: «Цепи переменного тока».

Цель работы: Изучение цепи переменного тока с параллельным соединением ветвей.

Оснащение

1. Электрическая цепь с параллельным соединением ветвей,

2. Схема электрической цепи.

Основные теоретические положения

В электрической цепи при параллельном соединении катушки и конденсатора на схеме их можно представить активными и реактивными проводимостями рис.1.

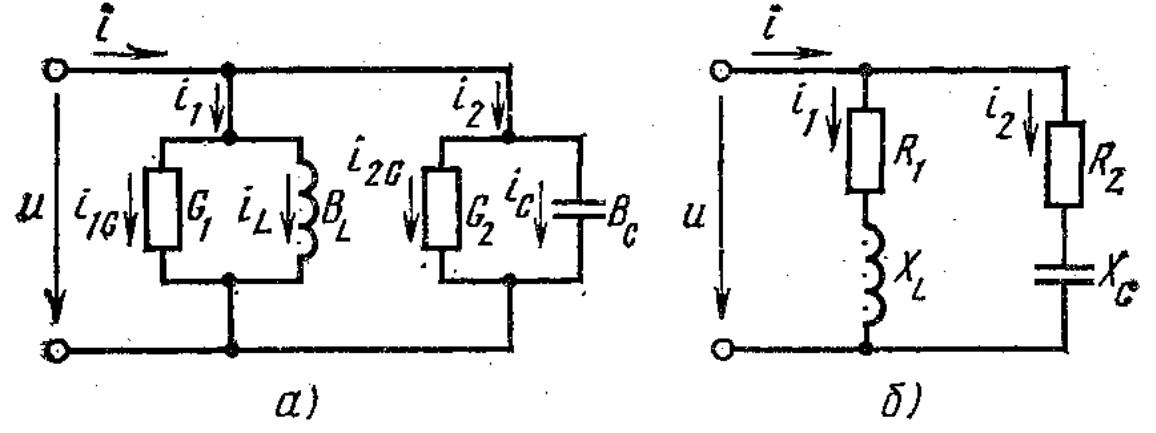Рис.1.

Но рис. а) предпочтительнее, т.к. в ней все элементы соединены параллельно, а в б) элементы соединены смешанно.

По первому закону Кирхгофа мгновенный общий ток будет равен:

(1)

Т.к. активные и реактивные токи по фазе не совпадают, то общий ток находится векторным сложением:

Порядок выполнения работы

1.Изучить теоретический материал.

2.Выполнить задание.

Задание 1. Для схемы рис.2 определить ток, активную, реактивную и полную мощность катушки, конденсатора и всей цепи при неизменном напряжении U = 200 В и частоте источника f = 100 Гц, R1 = 10 Ом, L= 55,2 мГн, С= 138 мкФ, R2 = 0.

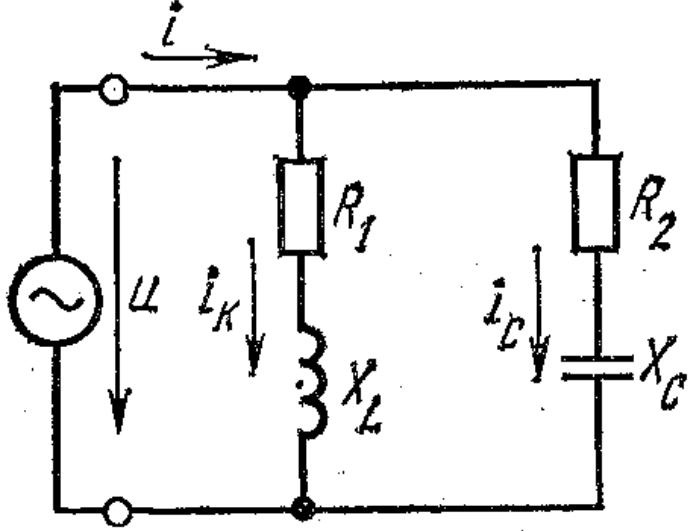Рис.2

Индуктивное сопротивление первой ветви равно .

Проводимости активная и реактивная равны: ; (См)

Полная проводимость катушки: (См).

Проводимости второй ветви активная и реактивная равны: (См)

Полная проводимость .

Токи:

в неразветвленной части цепи ,

в конденсаторе , в катушке

Коэффициент мощности цепи: ;

Реактивные мощности:

катушки , конденсатора , цепи

Активная мощность цепи

Полные мощности:

катушки , конденсатора , цепи .

Контрольные вопросы

1.Объясните выражение (1).

2.Как обозначаются проводимости?

Лабораторная работа №7 по дисциплине ОП 05. Теория ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Тема: «Цепи переменного тока».

Цель работы: Изучение цепи переменного тока с параллельным соединением катушки и конденсатора.

Оснащение

1. Электрическая цепь с параллельным соединением катушки и конденсатора,