0

Министерство образования и науки Украины

Севастопольский национальный технический университет

Методические указания

Стационарные случайные процессы. Построение модели фена

к проведению практических занятий

по дисциплине «Стохастический анализ» для студентов

дневной формы обучения

направления подготовки 0914 «Компьютеризированные

системы, автоматика и управление»

Севастополь

2011

УДК 62-52.001.24

Методические указания к проведению практических занятий «Стационарные случайные процессы. Построение модели фена» по дисциплине «Стохастический анализ» / Сост. Б.А. Скороход – Севастополь, 2011. – 8с.

Цель методических указаний – помочь студентам в изучении раздела курса случайные процессы.

Методические указания предназначены для студентов дневной формы обучения по направлению подготовки 0914 – «Компьютеризированные системы, автоматика и управление».

Методические указания рассмотрены и утверждены на заседании кафедры технической кибернетики

(протокол № от 2011 г.)

Рецензент: д.т.н., профессор Дубовик С.А.

Содержание

1. Краткие теоретические сведения 4

2. Описание объекта 6

3. Постановка задачи 7

4. Порядок выполнения и задание на работу 7

5. Содержание отчёта по работе 8 6. Контрольные вопросы 8

Библиографический список 8

Цель работы: Построение оценок характеристик стационарных случайных процессов по экспериментальным данным.

1. Краткие теоретические сведения

Известно, что исчерпывающей характеристикой случайной величины является ее закон распределения, который может быть описан с помощью функции распределения. Для задания случайного процесса (с.п.) используются многомерные функции распределения

,

которые должны быть определены для любых значений из области изменения . Теоретически можно неограниченно увеличивать число сечений, получая все более полное описание с.п. Однако оперировать с многомерными функциями сложно, а для их получения необходимы большие объемы экспериментальных данных, которые к тому же растут с увеличением количества сечений. Поэтому, в большинстве случаев, ограничиваются использованием основных характеристик с.п.: математического ожидания, корреляционной функции и дисперсии. Для непрерывного с.п. они определяются, соответственно, выражениями

,

,

,

где , - одномерная и двумерная плотности распределения с.п.

Случайный процесс называется стационарным в широком смысле, если его математическое ожидание и дисперсия постоянны, а корреляционная функция зависит от разности аргументов, т.е., . Для стационарного с.п. вводится понятие спектральной плотности, которая связана с корреляционной функцией соотношением

.

По спектральной плотности, может быть найдена корреляционная функция

.

Стационарный случайный процесс называется эргодическим, если любая его вероятностная характеристика, полученная усреднением по множеству возможных реализаций, с вероятностью сколь угодно близкой к единице равна соответствующей характеристике, полученной путем усреднения по времени на основании анализа любой реализации этого с.п. Для эргодического с.п. математическое ожидание и корреляционная функция определяются, соответственно, выражениями

,

,

где − реализация с.п. .

Стационарным белым шумом называют стационарный с.п. спектральная плотность, которого постоянна − . Можно показать, что корреляционная функция белого шума определяется выражением , где - дельта-функция

.

Таким образом, корреляционная функция стационарного белого шума пропорциональна дельта-функции; коэффициент пропорциональности называют интенсивностью белого шума.

Дельта-функция равна нулю при всех значениях , поэтому и корреляционная функция также равна нулю при этих же значениях. Равенство же нулю корреляционной функции белого шума означает некоррелированность любых двух его сечений. Благодаря этой особенности белый шум находит широкое применение в теории с.п. и ее приложениях. Однако эта же особенность указывает на то, что осуществить белый шум невозможно, так как в действительности при очень близких значениях соответствующие сечения коррелированны. Таким образом, стационарный белый шум - математическая абстракция, полезная для теории с.п. и ее приложений. В частности, белый шум используют для моделирования случайных процессов, которые имеют постоянную спектральную плотность в определенном диапазоне частот, причем поведение спектральной плотности вне его исследователя не интересует.

0. Пусть 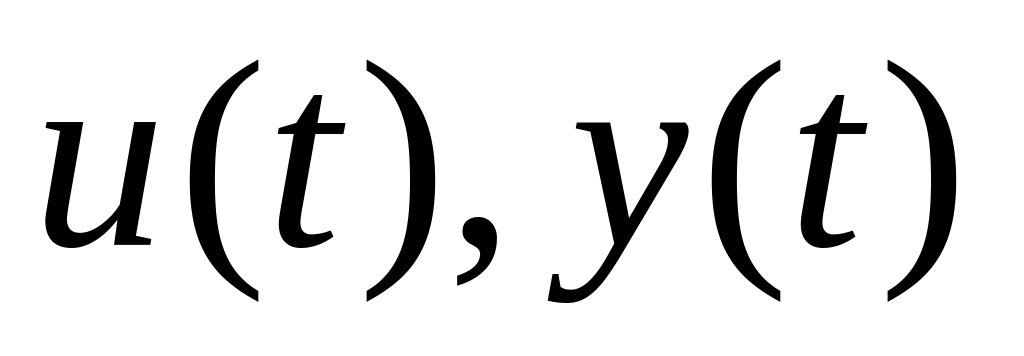обозначают входные и выходные сигналы некоторой системы, соответственно, в момент времени . Мы будем рассматривать значения этих сигналов только в дискретные моменты, распределенные равномерно на временном интервале с тактом дискретности . Предположим, что мы хотим описать, каким образом сигналы связаны между собой. Один из наиболее распространенных подходов состоит в использовании разностного уравнения

1. ,

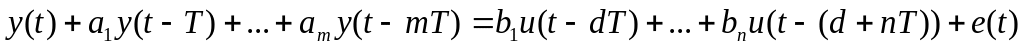которое называется моделью авторегрессии и скользящего среднего (АRХ), а величины ее параметрами. Требуется по экспериментальным данным оценить порядок модели – величины и ее параметры . Решение этой задачи может быть сведено к выбору параметров из условия минимумы критерия

при каждом фиксированном наборе , где ,

.