2Көлемдік тұрақты тоқтың магнит өрісінің кернеулігі.

Оны анықтау үшін электр өрісінен үзындығы -ға, қимасы ауданы -тең болатын цилиндр кесіп аламыз.Егер щилиндрден ағып өтетін ток шамасы, сол цилиндр ұзындығымен бағытталған ток тығыздығымен анықталса, онда ток элементі болып - -көбейтіндісі алынады. Ал бұл ток элементі тудыратын -қашықтықтағы магнит өрісі кернеулігі Био-Савар заңы бойынша былай анықталады:

dH = . (6.4)

dldS₀-көбейтіндісін -цилиндр көлемімен алмастырып, ал ток элементі бағытын ток тығыздығы бағытымен байланыстырамыз. Онда (6.4) теңдеу векторлық түрде былай жазылады.

d = = ; (6.5)

(5) теңдеуді интегралдау арқылы тогы бар көлемдік өткізгіш тудыратын магнит өрісінің кернеулігін анықтаймыз:

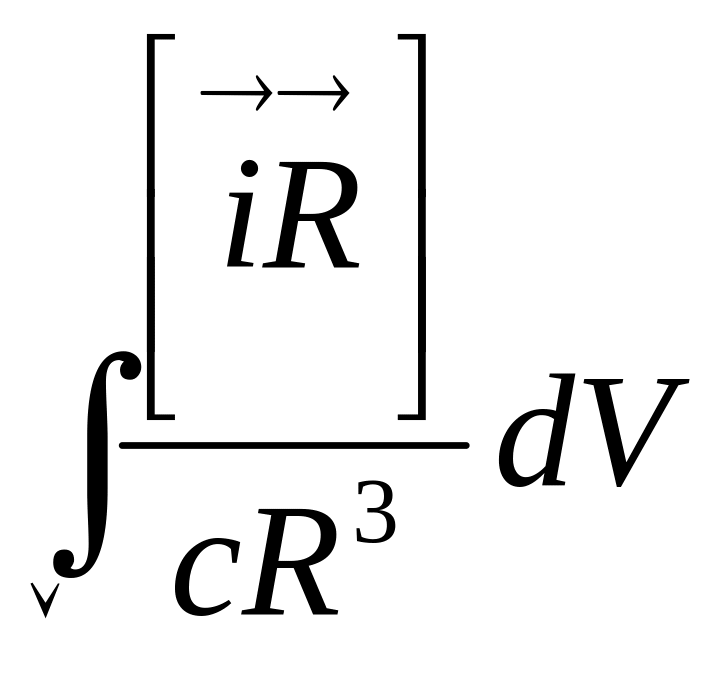= . (6.6)

3Скалярлы өрістің градиентін есептеу

;

Ответ:

7 Билет

1 Гриннің фундаменталды өрнегі

Бұл өрнек Гриннiң екiншi өрнегiнен алынады. Ол үшін мынандай екі скалярлы функцияны қарастырамыз:

=U , = V= 1/r ,

мұндағы r - көлем элементi d және беттiк элемент dS-тан қарастырылып отырған P нүктесiне дейiнгi арақашықтық. Бұл жағдайда Гриннiң екiншi өрнегi былай жазылады:

. (14.1)

Сурет 1.

Б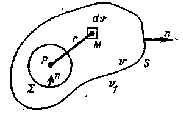 ұл алынған (14.1) теңдiктi үш түрлi жағдайда қарастырамыз, мұнда облысы S бетiмен шектелген деп есептейміз (Сурет ).

1 ) P нүктесi S бетiнiң сыртындағы ₁ кеңiстiгiнде жатады.

Бұл жағдайда беттiң iшiнде жатқан кез-келген М нүктесi үшiн 1/r- функциясы Лаплас теңдеуiн қанағаттандырады, яғни :

. (14.2)

Егер функциясынан екі реттен координаталар бойынша туынды алатын болсақ: х координатасы бойынша бірінші туынды - ;

екінші туынды - .

Осылай келесі координаталардан да екі реттен туынды аламыз:

,

.

Сонымен (25) өрнек былай жазылады :

.

Олай болса (14.1) өрнектің сол жағындағы интеграл ішіндегі мүшенің бірі нольге айналады: = 0. Мұны ескере отырып, кеңістігінде кездесетін жағдай үшін Гриннің екінші өрнегін былай жазамыз:

(14.3)

2) P нүктесi облысының iшiнде жатсын. Бұл жағдайда Грин өрнегiн бүкiл облыс үшiн қолдануға болмайды. Себебi :

Егер P нүктесi М нүктесiмен сәйкес келетін болса, 1/r –функциясы сол нүктеде үзiледi. Сондықтан P нүктесiн сфералық бет  арқылы қоршаймыз. Сол кезде облысының  сфералық бет арқылы қоршалған бөлімінен басқа (жер) бөлiктерi үшiн Грин өрнегiн қолдануға болады.

(14.4)

Мұндағы ₂ облысы сферамен қоршалған бөлiктi шығарып тастағандағы облысы болып есептелінеді. (14.4) өрнектегі интегралдарды жеке қарастырамыз.

А/ Беттiк интеграл S және  беттерi арқылы алынады. Егер  сфералық беттi шексiз қысатын болсақ, ол P нүктесiне ұмтылады, олай болса ₂ –көлемi бойынша алынған интеграл -көлем бойынша алынған интегралға айналады, яғни :

Б/ Енді (14.4) теңдiктiң оң жағындағы соңғы екi интегралдың мәнiн қарастырамыз. Егер ₂ көлемiне қатысты сыртқы нормаль n - сфералық бетi үшiн iшкi нормаль болатын болса, онда ол сфера радиусымен сәйкес келеді, соңғы екі интеграл былай жазылады:

Бұл жағдайда сфералық бет бойынша алынған интегралдар шегi былай есептелiнедi:

Сфера беті нольге ұмтылғанда U функциясының шамасы P нүктесiндегi мәнге U(P) ие болады.

Соңғы теңдіктің оң жағындағы бірінші интеграл шегіде нольге ұмтылады, себебі бет элементі dS сфера үшін г² тура пропорционал, онда интегралдағы (1/г)dS функциясы r-сфера радиусына тура пропорционал шама болады. Олай болса r , интеграл мәнi де нольге ұмтылады.

Сонымен (14.4) теңдiктi шектiк жағдайда қайта жазатын болсақ, ол мынандай түрде жазылады:

3) P нүктесi S –бетiнде жатсын (PS).

Бұл жағдайда жоғарыда көрсетiлгендей етiп талдау жасайтын болсақ, (14.5) өрнек тәрiздi теңдеу аламыз, ал оның оң жағы 2U(P) шамасына тең болады. Себебi, сфера бетi бойынша алынатын интегралдың бәрi жартылай сферадан есептелiнедi. Олай болса Гриннiң өрнегi былай жазылады:

Сонымен қарастырылған үш жағдайда қортындылайтын болсақ, Гриннiң екiншi өрнегiн жалпы түрде былай жазамыз:

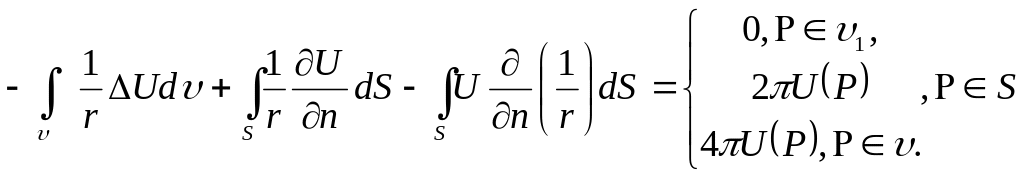
Бұл (7)-өрнек Гриннiң фундаменталды өрнегi деп аталынады.

Сол жақтағы интегралдардың физикалық мәндері бар :

А) бірінші интеграл – көлемдік массаның тартылыс потенциалы, егер - облыс ішіндегі тартылыс тудыратын массаның таралу тығыздығына тең болса, оны қысқаша деп белгілейміз;

Б/ екінші интеграл – жәй қабаттың тартылыс потенциалын анықтайды, егер беттегі ( S) массалардың таралу тығыздығын анықтайтын болса, онда оны қысқаща деп белгілейміз;

В/ үшінші интеграл қос қабаттың тартылыс потенциалы, егер S бетіндегі әрбір нүктедегі момент шамасы U -ға тең болса, оны деп белгілейміз.

Сонымен, Гриннiң фундаменталды өрнегiнiң сол жағы үш түрлi тартылыс потенциалының қосындысынан тұрады екен, ол - көлемдiк масса, жәй қабат, қос қабаттың тартылыс потенциалдары, яғни:

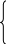-U₁(P) +U₂(P) – U₃(P) =

Мынадай жеке жағдайларды қарастырамыз:

1. Е 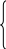гер U функциясы гармоникалық болатын болса, онда U=0, ал (14.7) теңдеуде жай қабат пен қос қабаттың тартылыс потенциалдары ғана қалады:

U₂(P) – U₃(P) =

2. Егер U=1, онда ол функцияның нормаль бағыттағы туындысы нольге тең, яғни U/n=0, онда (7 ) теңдеу мына түрде жазылады:

=

Интеграл астында 1/r-функциясынан нормаль бойынша алынған туынды тұр, оның геометриялық мағынасы бар, ол P нүктесiнен беттiк элемент dSтің көрiну бұрышын анықтайды. Бұл өрнек - Гаусс өрнегі делінеді.