6 Билет
1 Векторлық өрістер оның туындылары.(дивергенция, ротор )
Векторлыќ µріс деп єрбір н‰ктесіне бір векторлыќ шама сєйкес келетін кењістіктіњ бір бµлігін айтамыз.
Векторлыќ µріс векторлыќ сызыќ арќылы кескінделеді, м±ндай сызыќтыњ єрбір н‰ктесіне ж‰ргізілген жанама µріс векторымен баѓыттас болады.
Векторлыќ сызыќтарѓа перпендикуляр баѓытта ж‰ргізілген жазыќтыќтар нормаль жазыќтыќтар деп аталынып, олар арќылы да векторлыќ µрісті сипаттауѓа болады.
Векторлыќ сызыќтарѓа параллель баѓытта ж‰ргізілген сызыќтар жиынтыѓы векторлыќ жазыќтыќты ќ±райды. Егер векторлыќ сызыќ т±йыќ болса, онда векторлыќ жазыќтыќ т±йыќтаѓан кењістік векторлыќ т‰тікше деп аталынады. Оныњ кµлденењ ќимасы болып, т‰тікшеніњ нормаль жазыќтыќпен ќиылысы саналады.
Сонымен, векторлыќ µріс: векторлыќ сызыќ, нормаль жазыќтыќ немесе векторлыќ жазыќтыќтар арќылы кескінделеді.
¤рістегі векторлыќ шаманыњ бір н‰ктеден екінші н‰ктеге µзгеру жылдамдыѓы – сол векторлыќ функцияныњ алынѓан баѓыттаѓы туындысы арќылы µрнектеледі. Сондыќтан оны туынды ережесі бойынша былай жазамыз:
,
(2.1)
м±ндаѓы
векторлыќ функцияныњ
н‰ктелеріндегі мєні;
екі н‰кте арасындаѓы ќашыќтыќ. Б±л
туынды векторлыќ шама. Ал µрісті сипаттау
‰шін векторлыќ функциядан бір –біріне
перпендикуляр ‰ш баѓытта алынѓан
туынды жеткілікті, яѓни:
О
сыѓан
байланысты векторлық
өріс - үш скалярлы өріс қосындысымен
анықталады. Ал єрбір скалярлы µріс
скалярлы функциядан бір-біріне
перпендикуляр баѓытта алынѓан ‰ш
туындымен сипатталады. Олай болса, бұл
өрістің дифференциалды сипаттамасы –
болып тоғыз туындыдан тұратын тензорлы
өріс саналады:
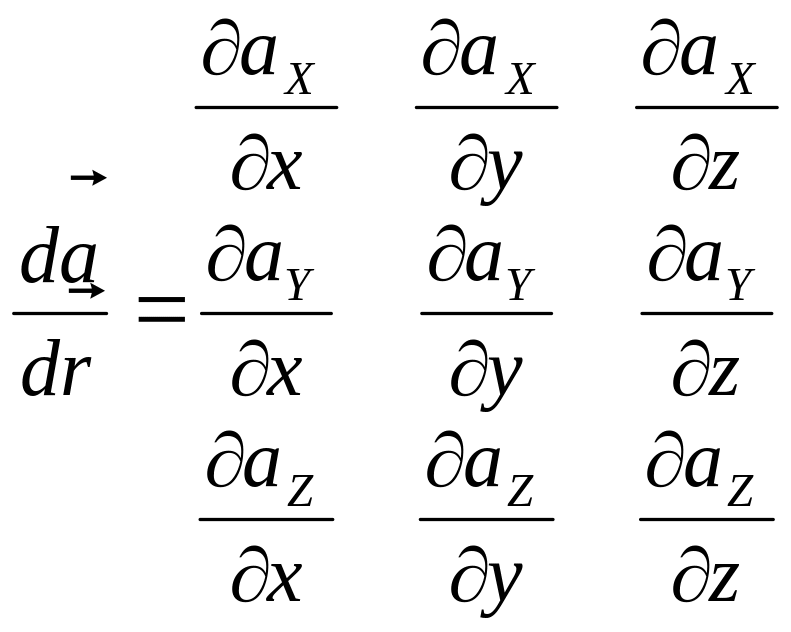(2.2)
Векторлық өрісті берілген (2) тензор туындының инварианттары арқылы сипаттауға болады, яғни тензорлы шама орнына қарапайым векторлық және скалярлық шамалар қолданамыз.
Бірінші инвариант – тензор туындының диагональ бойымен орналасқан элементтерінің қосындысынан тұратын скалярлық шама, оны векторлық өрістің дивергенциясы деп атаймыз:
= ах/х + ау/у + а z/z .
Сонымен, дивергенция - векторлық өрістің көлемдік туындыларының бірі болып есептелінетін скалярлы шама. Ол өріс көзінің тығыздығын анықтайды. Өрісті кескіндейтін векторлық сызықтар осы көздерден таралып немесе соған жинақталады.
Екінші инвариант - тензор туындының антисимметриялық бөлігінен тұратын векторлық шама, оны – векторлық өрістің роторы деп атаймыз.
Оны ашып жазу ‰шін берілген тензор-туындыны симметриялыќ жєне антисимметриялыќ бµлікке жіктеп, оныњ антисимметриялыќ бµлігін ќарастырамыз:
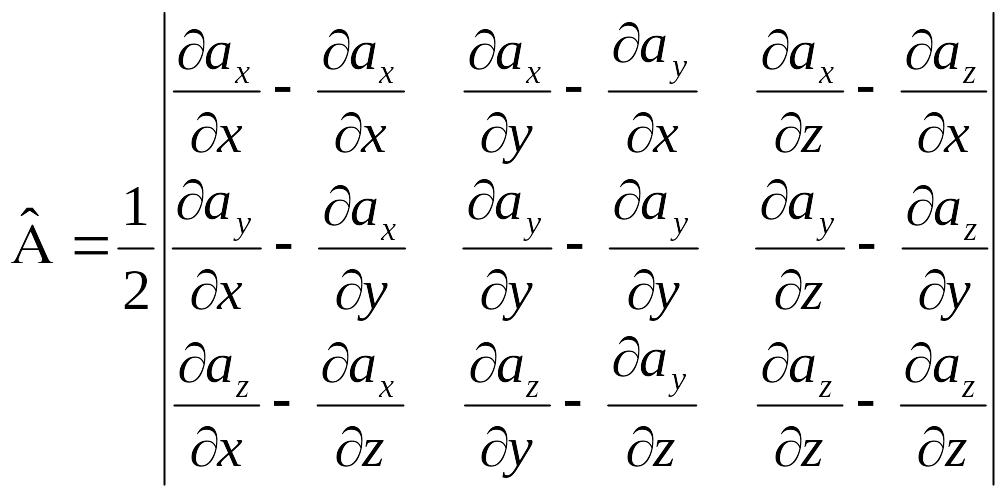
Б±л матрицадаѓы диагональ бойынша элементтер ќосындысы нольге айналады, ал ќалѓан м‰шелері оњ жєне теріс тањбалы ‰ш скалярлы шама бола алады. Б±л скалярлы ‰ш шаманы бір вектормен алмастыруѓа болады, себебі кез келген вектордыњ декартты координаталар системасында ‰ш проекциясы бар. Б±л векторды µрістіњ роторы немесе ќ±йыны деп атап, оны проекциялары арќылы былай жазамыз:
=
.
Сонымен, векторлық өріс роторы - өріс жазықтығына перпендикуляр бағытталған вектор, оның шамасы - өріс көзі құйынының тығыздығын анықтайды. Декартты координаталар системасында оны үшінші дәрежелі анықтауыш ретінде былай өрнектейді:
.
Векторлық өрістің дифференциалды сипаттамалары ретінде скалярлы шама – дивергенцияны, векторлық шама - роторды қолданамыз.