2 Тұрақты токтың біріккен заңы

(5.5) жэне (5.8) өрнекпен анықталатын Ом және Кирхгоф заңын біріктіруге болады, бірақ ток тығыздығын жалпы түрдегі өрнекпен = ( + _ст ) аламыз, мұндағы электр өрісі кернеулігін скалярлы потенциалдың градиенті ретінде теріс таңбамен алсақ, = - , онда Кирхгофтың 1-заңын былай жазамыз :

div = 0, div ( grad U - _ст ) = 0,

Е_ст = 0, онда тұрақты ток үшін бұл теңдік былай жазылады:

div grad U = 0,

ал өткізгіш изотропты болса, онда = const, сондықтан теңдеу мына түрге ие болады:

div grad U = U = 0.

Демек, біртекті изотропты өткізгіштегі токтың электр өрісінің потенциалы Лаплас теңдеуін қанағаттандыруы қажет.

Ал анизотропиялық орта үшін біріккен заң былай жазылады:

div[ _xx - E_{x ст} + _уу - Е_{у ст} ) + _zz ( - E_{z ст} )] = 0. (5.15)

Бұл теңдеулер белгілі бір шекаралық шарттарда ғана шешіледі, ол шешім дүрыс және жалғыз ғана болады. Демек, дифференциалды теңдеу шешімі шекаралық шарттармен анықталады. Мынандай шекаралық шарттар бар:

1) бір беттен екіншіге өткенде жапсарда потенциалдың үзілуі э.қ.к.-тең, яғни :

U₂ – U₁ = Е_21;

1. жапсарда ток тығыздығының нормаль құраушысы үздіксіз, яғни жапсарға қанша ток келсе, сонша ағып өтеді, демек: i_n1 = i_n2.

3тартылыс потенциалын есептеу F= v=?

F=

V= Ответ:V=

5билет

1 Өрістің потенциалды және квазипотенциалды болу шарттары.

Грин өрнектері потенциалды жєне квазипотенциалды µрістерге арналѓан. Сондыќтан мұндай µрістерге аныќтама беріп, олардыњ потенциалды жєне квазипотенциалды болу шарттарын ќарастырамыз.

Векторлы өрісті потенциалды дейміз, егер оныњ векторы скалярлы функцияның градиенті ретінде аныќталатын болса, яѓни : , м±ндаѓы скалярлы функция - векторлы µрістіњ скалярлы потенциалы деп аталынады.

өрістің потенциалды болуыныњ мынандай шарттары бар:

1 Өрістің потенциалды болуының қажетті және жеткілікті шарты болып µріс векторынан кез –келген ќисыќ бойымен алынѓан интеграл шамасының ќисыќтыњ бастапќы жєне соњѓы н‰ктелеріне ќатысты потенциалдар айырмасымен аныќталуы жатады:

,

яѓни интеграл шамасы ќисыќ т‰ріне байланысты емес.

2. Өрістің потенциалды болуының қажетті және жеткілікті шарты болып өріс векторынан алынған ротордың нольге айналуы жатады. Соњѓы µрнекті т±йыќ ќисыќпен алатын болсаќ, Стокс тењдеуін жазамыз:

.

тењдіктіњ сол жаѓындаѓы интеграл нольге айналады, себебі интегралдаудыњ бастапќы жєне соњѓы н‰ктелері бір-біріне сєйкес келіп т±р, сондыќтан оњ жаќтаѓы интеграл да нольге айналады. Олай болса интеграл астындаѓы шама нольге тењ болу керек, яѓни . М±ндай µрістер циркуляциясыз, ќ±йынсыз болады.

.

¤рісті квазипотенциалды дейміз, егер оныњ векторы скалярлы функцияны басќа бір скалярлы функцияның градиенті болатын векторға кµбейту арќылы аныќталатын болса, яѓни:

, (3.11)

ал оныњ ќ±раушылары былай аныќталады:

.

¤рістіњ квазипотенциалды болуының қажетті және жеткілікті шарты болып өріс векторы роторының өріс векторына көбейтіндісі нольге тең болуы жатады, яғни:

2 тұрақты тоқтың магнит өрісі, сызықтық күш үшін био совар заңы.

Тақырыбы: Тұрақты токтың магнит өрісі. Био-Савар заңы.

Дәріс конспектісі:Тұрақты электр тогын тудыратын зарядтардың реттелген қозғалысы уақыт бойынша тұрақты магнит өрісін тудырады. Бұл өрістің кернеулігі Био-Савар заңы бойынша анықталады, ол ток элементіне арналған. Сондықтан өткізгіштің сызықтық, көлемдік, жазықтық болып келуіне байланысты Био-Савар заңының жазылымы да әртүрлі.

а) Сызықтық токтың магнит өрісі

Сызьқтық өткізгіште тұрақты электр тогы болсын. Одан ұзындығы -тең элементар өткізгіш кесіп қарастырамыз. Токтың элементар өткізгіш ұзындығына көбейтіндісін -ток элемент дейміз. Био-Савар заңы бойынша ток элементінің -қашықтықта тудыратын магнит өрісінің кернеулігі мына өрнекпен анықталады:

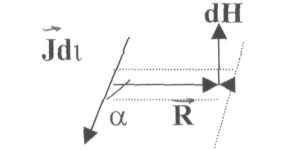dH =

Мұндағы: с-электродинамикалық тұрақтылық, сандық мәні вакуумдегі жарық жылдамдығына тең; -қарастырылған нүктеге дейінгі арақашықтық; -ток элементі мен -радиус вектор арасындағы бұрыш.

Бұл (6.1) теңдеуді векторлық түрде жазуға болады. Ол үшін -ға ток бағытын береміз, ал -векторын ток элементінен қарастырылатын нүктеге қарай бағыттаймыз. Сонда магнит өрісінің бағыты бұранда ережесімен анықталып, былай жазылады:

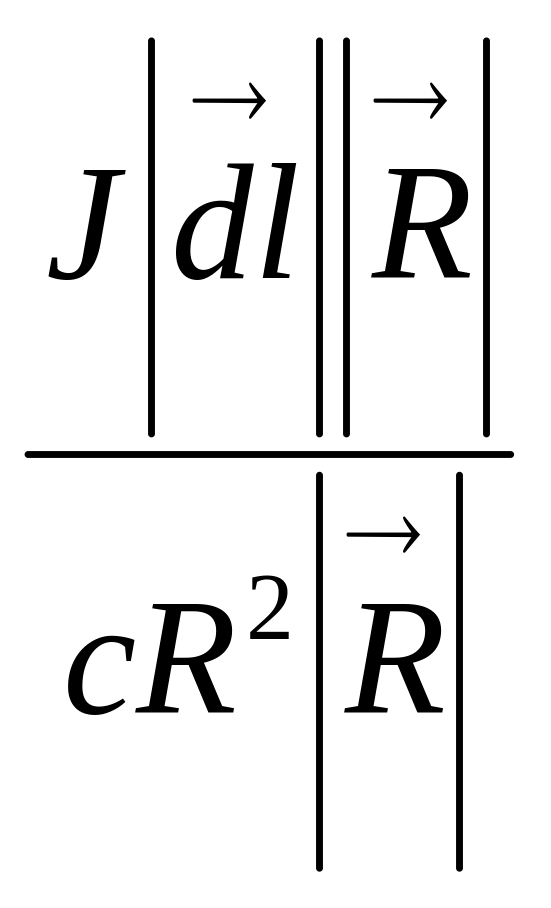= sin = ; (6.2)

Кернеулік векторы ток элементі және векторлары құрайтын параллелограмм жазықтығына перпендикуляр. Егер (6.2) теңдеуді бүкіл өткізгіш ұзындығымен интегралдайтын болсақ, онда сызықтық токтың магнит өрісінің кернеулігін аламыз, яғни:

= . (6.3)

в)Жазық токтың магнит өрісі

Егер электр тогы жазьқтық арқылы өтсе, онда ] жазықтықтағы

ток тығыздығы ұғымын енгіземіз. Жазықтықтан ұзындығы , ені болатын аудан кесіп аламыз. -қашықтықтағы нүктеде ток элементі - -магнит өрісін тудырады, оның кернеулігі Био-Савар заңы бойынша былай анықталады:

dH = . (6.7)

-көбейтіндісін -ауданымен алмастырып , ток элементі бағытын -векторы бойынша анықтап, (6.7) теңдеудің векторлық жазылымын аламыз:

d =

(6.8) өрнекті бет бойынша интегралдап жазық ток тудыратын магниттік өрістің кернеуін аламыз:

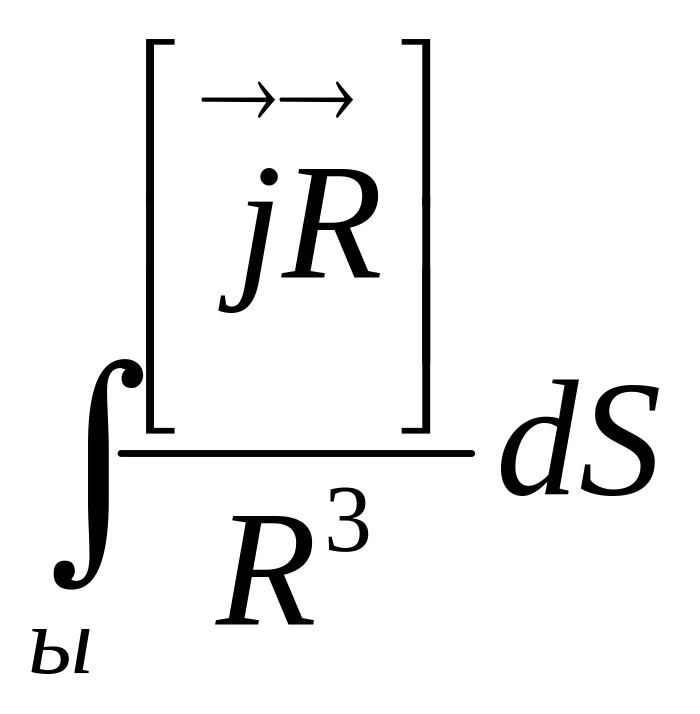= . (6.8)

Векторльқ потенциал.

Магнит өрісін Био-Савар заңынан басқа векторлық потенциал арқылы да есептеуге болады. Ол үшін магнит өрісіні кернеулігін потенциал арқылы өрнектейді, яғни : = rot . (6.9)

Векторлық потенциал өрісті зерттеуін жеңілдететін көмекші векторлық функция. Сонымен қатар соңғы өрнекті векторлық потенциалды өріс кернеулігі арқылы өрнектеу деп те түсінуге болады. Сондықтан магнит өрісі кернеулігі электр тогы арқылы анықталғандықтан, векторлық потенциал да ток арқылы мына өрнектермен анықталады:

= ; (6.10) = ; (6.11)

= ; (6.12).

Векторлық потенциал да скалярлы потенциал тәрізді Лаплас немесе Пуассон теңдеулерін қанағаттандырады, тек айырмашылығы көздері векторлық шама болады:

=

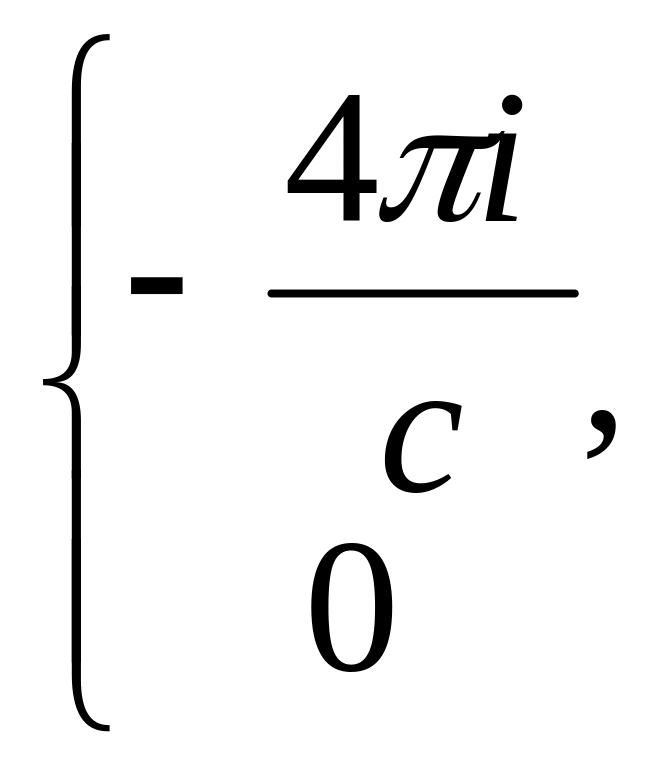
немесе декартты координаталар системасында вектор проекцияларына арналған теңдеулер былай жазылады: А_х =

= = .

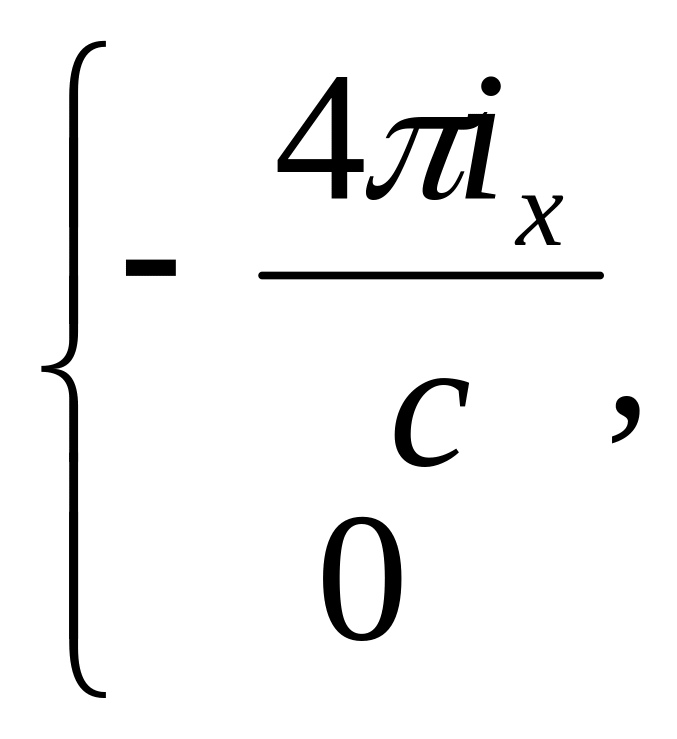
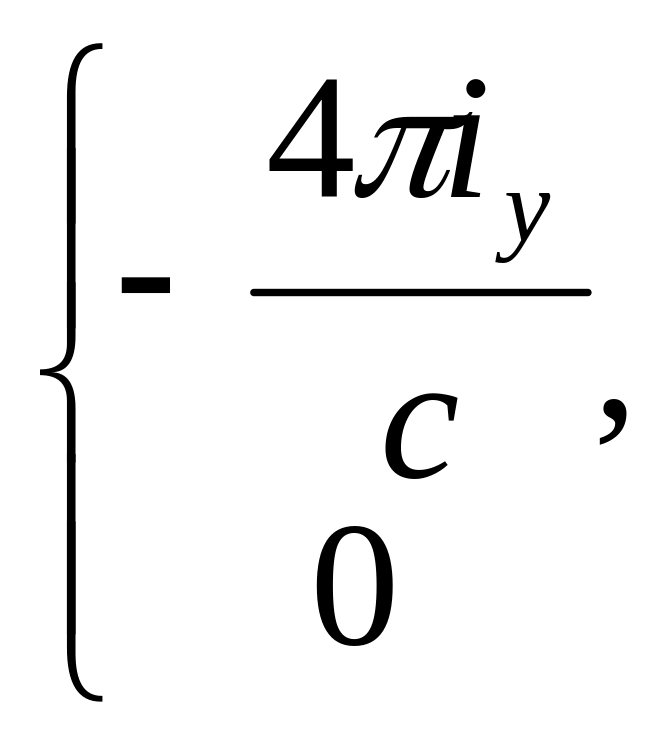
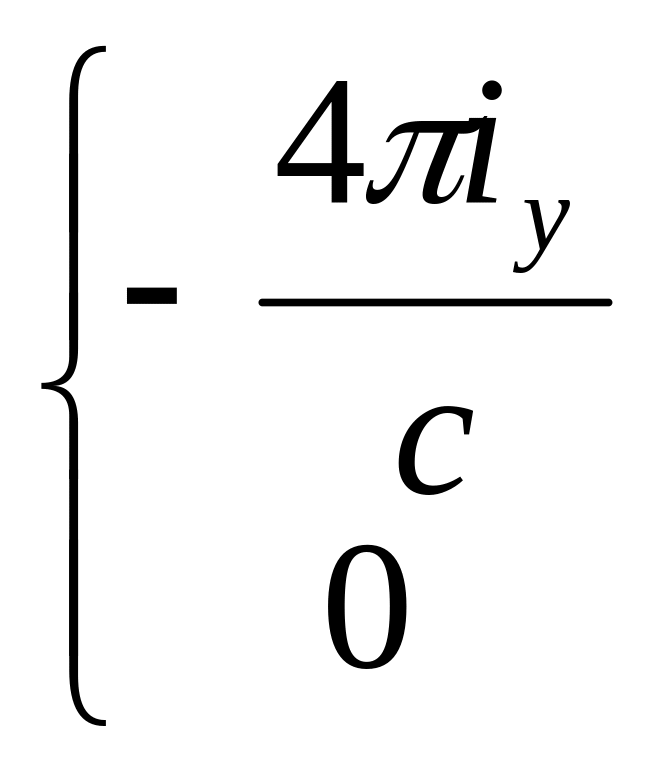Сонымен қатар (6.9) өрнектің екі жағынан да құйын аламыз, онда rot = rot rot . Өрнектің оң жағы векторлық ереже бойынша жіктеледі:

rot rot = grad div - , егер өрістің түтікшелі екенін еске алсақ div = 0 , онда :

rot =- - немесе rot = . (6.13)

Бұл Био-Савар заңының дифференциалды жазылымы, ол тұрақты ток тудыратын магнит өрісінің құйынды екенін көрсетеді..

Егер (6.13) теңдеудің екі жағынан да бет бойынша интеграл алсақ, онда:

= .

Бұл интегралдың сол жағы Стокс теоремасы бойынша магнит өрісінің кернеулігінің циркуляциясын береді, ал оң жағы ток шамасын көрсетеді. Олай болса:

= . (6.14)

Бұл Био-Савар заңының интегралды жазылымы.

Тұрақты ток тудыратын магнит өрісі құйынды болғанмен, тогы жоқ нүктелерде ол құйынсыз. Сондықтан оны скалярлы потенциал арқылы да зерттеуге болады. Бұл жағдайда магнит өрісінің кернеулігін былай көрсетеміз:

= - grad U . (6.15)

Егер бұл теңдіктің екі жағынан да дивергенция алсақ, онда мынандай жазылым аламыз:

div = - = - = 0 немесе U = 0.

Соңғы теңдіктен скалярлы потенциалдың Лаплас теңдеуін қанағаттандыруы қажет екені байқауға болады.

3 тартылыс потенциалын есептеу ;

;

; Ответ: