22Билет

1 Серпiндiлiк кернеуiнiң тензоры . Кернеулік векторы ( ) жалпы жағдайда берілген ауданға перпендикуляр болмауы да мүмкін. Осыған байланысты қарапайым деформация түрлерін қарастырғанда кернеулік векторын нормаль және жанама кернеуліктерге жіктедік. Сондықтан кернеулік векторы түсірілген нүктені қамтитын ауданның бағытына байланысты анықталады. Осы жағдайға қатысты бұл векторға ауданның бағытын көрсететін индекстік көрсеткіш коямыз.

Ж алпы алғанда, денедегі кез келген нүктені қамтитын ауданды сансыз көп бағытта алуға болады, яғни берілген нүктеге түсірілген кернеулікті де сансыз бағытта қарастыруға болады. Бірақ, денедегі деформацияны сипаттау үшін бір-біріне перпендикуляр үш бағытта алынған ауданға түсірілген кернеулік векторлары жеткілікті болады. Егер бір-біріне перпендикуляр аудандардың нормалі ОХ, ОУ, ОZ координата осьтерімен сәйкес келетін болса, онда кернеулік векторлары мынандай үш вектор арқылы өрнектеледі: _х, _у, _z. Көрсетілген үш вектордың әрқайсысы декартты координаталар системасында өзінің үш проекцияларымен сипатталады, яғни проекцияларда екі индекстік көрсеткіш жазылады, біріншісі – ауданның бағытын көрсетсе, екіншісі – проекцияның (құраушының) бағытын көрсетеді.

Сонымен тоғыз құраушыдан тұратын кернеулік – серпінді кернеулік тензорын құрайды:

.

Матрицаның горизонталь бiр қатарында бiр вектордың х, у, z осьтерi бойынша проекциялары жинақталған. Матрицаның диагоноль бойымен орналасқан элементтері (P_xx, P_уy, P_zz ) – нормаль кернеулiктер немесе негiзгi кернеулiктер, ал қалған симметриялы элементтері (Р_ху, Р_хz, Р_уz ) - жанама кернеулiктер болып есептелiнедi.

Негiзгi кернеулiктер созылу мен қысылу деформациясын тудырады, ал жанама кернеулiктер – ығысу деформациясына алып келедi. Сонымен, кернеулiк тензоры матрицаның басқы диагонолына қарағанда симметриялы болып, берiлген нүктедегi кернеулiкті толық сипаттайды.

2Қос қабаттың логарифмдiк потенциалы

Жазық қос қабатты - жазық дипольдан тұрады деп есептеуге болады, егер оларды цилиндрлiк бетке бiр жағына оң , екiншi жағына терiс таңбалы масса орналасатындай етiп жайғастыратын болсақ . Онда ені болатын кішкене жолақты элементар диполь деп десек, оның моментi былай анықталады:

dр= d .

Онда элементар қос қабат потенциалын мына өрнекпен жазамыз :

Жазық қос қабат потенциалы элементар диполь потенциалдары қосындысынан тұратын болғандықтан, оны бұл өрнекті интегралдау арқылы аламыз:

.

3 = y

div =

23 Билет

1Деформация тензоры

Деформация тензоры. Элементар бетке түсiрiлген кернеулiктi қарастыра отырып, осы бөлiктегi деформацияны сипаттаймыз. Олардың арасындағы байланыс арқылы Гук заңының жалпы түрдегі жазылымын аламыз.

Қ арапайым созылу және ығысу деформациялары салыстырмалы деформацияның бүкiл дене бойынша тұрақтылығымен сипатталады.Ол - дене пiшiнiнiң дұрыстылығына, түсiрiлген күштердiң бiрқалыптылығына және бекiтiлу жағдайларына байланысты.

Жалпы жағдайда деформация дененiң бiр нүктесiнен екiншiсiне өзгерiп отырады, яғни салыстырмалы деформация тұрақты шама бола алмайды. Сондықтан деформацияны белгiлi нүктеге ғана қатысты қарастыру қажет. Осыған байланысты берілген нүкте маңайындағы дененің көлемi мен пiшiнiнiң өзгеруiн қарастырамыз. Бұл жағдайда дененiң деформацияға ұшырау дәрежесiн векторлық шама да, скалярлық шама да өрнектей алмайды. Оны өрнектеу үшiн күрделi шама тензор қажет.

Осыған байланысты декартты координата системасында дененi деформацияға дейiн, және деформациядан кейiн қарастырамыз . Бұл деформацияны математикалық түрде өрнектеу үшiн дененiң әрбiр нүктесiне ығысу векторын сәйкес қоямыз:

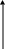
, (11.2)

мұндағы және - нүктенің орын ауыстырғаннан кейінгі және орын ауыстырғанға дейінгі радиус-векторлары.

Демек, деформация ығысу векторының U( r) өрiсiмен сипатталады. Бiрақ жеке нүкте үшiн алынған ығысу векторы деформацияны сипаттай алмайды. Сонымен қатар қарастырылып отырған нүкте мен оған көршi нүктелер ығысу векторына (U) тең шамаға орын ауыстырса, онда да деформация байқалмайды. Әрбiр нүкте маңындағы ығысу векторының салыстырмалы өзгерiсi ғана деформацияны береді. Демек деформация векторлық өрістің өзгеру жылдамдығымен анықталады. Ол векторлық функция болып есептелінетін ығысу векторынан векторлық аргумент бойынша толық туынды алуға алып келеді, оны тензор –туындыны деп атаймыз:

.

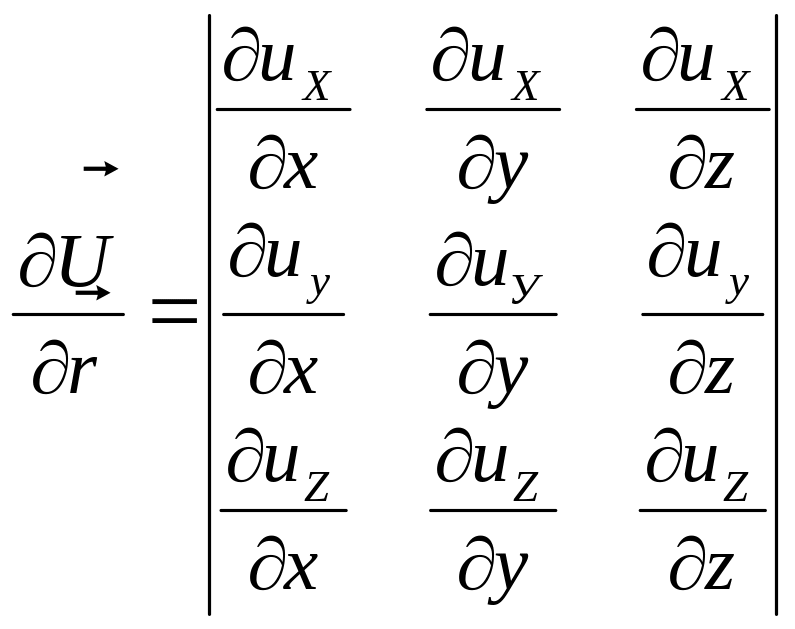Бұл тензор симметриялы емес, сондықтан оны симметриялы және антисимметриялы бөліктерге жіктеуге болады:

= .

Бұл тензордың А- антисимметриялық бөлiгi векторлық өрiстiң роторын сипаттайды. Қарастырылып отырған деформация жағдайы үшiн ротор болып бұратылу векторы алынады, ол мына өрнекпен анықталады:

,

яғни бұл вектор ығысу векторының ( ) құйынды бөлiгiн сипаттап, көлем элементінің кеңістіктегі бұратылуын көрсетеді.

Ығысу векторы өрісінің потенциалды бөлігі тензордың симметриялық түрімен( ) сипатталады, оны деформация тензоры деп атаймыз:

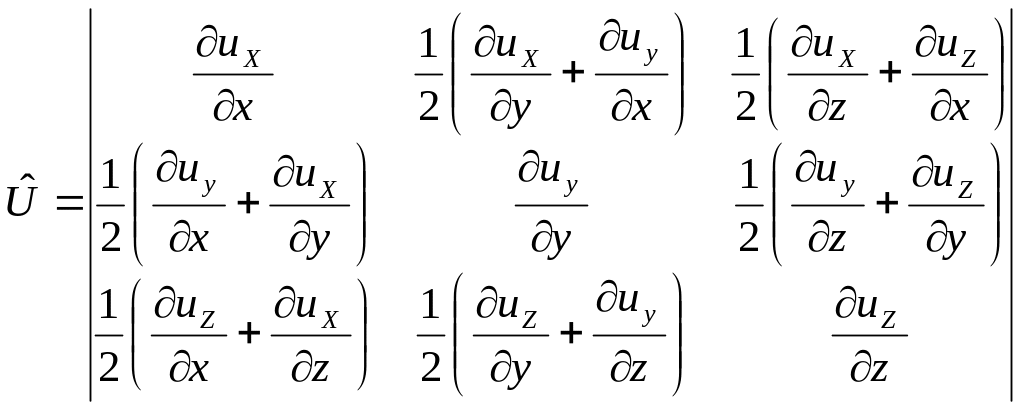
Деформация тензорының диагональ бойынша орналасқан элементтері ( ) оның негізгі шамалары деп аталынып, деформацияға дейін координата осьтеріне параллель бөліктердің салыстырмалы ұзаруын көрсетеді.

Ал бұл тензордың симметриялы компоненталары- - ығысу деформациясын сипаттайды.

Көлемнің салыстырмалы деформациясы (кеңею мен қысылу) ығысу векторының дивергенциясы ретінде анықталады:

.