17 Билет

1Өзкктің созылуы, гук заңы

Тәжірибеде өте жете зерттелген деформация болып - дөңгек қимасы бар өзектің немесе сымның тартылуы саналады.

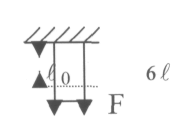
Өзектің жоғарғы бөлігін бекітіп, оның төменгі бөлігінің бүкіл көлденең қимасына бірқалыпты етіп, тартушы F-күшін түсірейік. Тәжірибеге сәйкес күшітің мәні өскен сайын оған пропорционал - өзектің ұзаруы да өседі, қаттылық шегіне жеткенше бұл процесс жүре береді.

Егер бұл заңдылықты графика түрінде кескіндесек, ол былай кескінделеді:

1) оа-бөлігінде күш пен деформация арасындағы пропорционалдық сақталады;

2) ав- бөлігінде деформация әсерінен өзек созылуы күштің өсуіне қарағанда тезірек жүреді;

3 )вс—бөлігінде күш түсірмеген жағдайдың өзінде өзектің созылуы жүреді, яғни деформация ұлғаяды. Бұл құбылыс дененің пластикалық агуы деп аталынады;

4) с- нүктесіне жеткенде дене қатаяды, оны созу үшін тағы да күш жұмсау қажет;

5) d - нүктесінде дене бұзыла бастайды, енді ешқандай күшті көбейтпей -ақ, оны азайтқан жағдайда да дененің жіңішкерген жерлерінен оның үзілуін байқауға болады.

Сонымен өзектің деформациясын тәжірибе жүзінде зерттей отырып, атақты ғалым Гук мынандай заңдылық ашты:

=  Р ₀ , (10.1)

яғни өзектің ұзару шамасы түсірілген кернеулікке тура пропорционал деген тұжырымға келді.

Мұндағы: - өзектің алғашқы ұзындығы, - дененің сызықтық созылу коэффициенті; Р - созушы кернеулік, оның мәні сыртқы түсірілген күштің өзектің көлденең қимасының ауданына қатынасымен өлшенеді, яғни: Р= .

Сызықтық созылу коэффициентіне кері шаманы созылу модулі немесе Юнг модулі дейміз, оның мәні мына өрнекпен анықталады: : Е = .

Онда ұзарған өзектің ұзындығы деформациядан кейін мына өрнекпен анықталады:

= ₀ (1+P) = ₀ + ,

Мұндағы: P = - өлшем бірлігі жоқ, бірден кіші шама. Себебі созылу модулін Е- кернеуліктің өлшем бірлігімен алу қалыптасқан.

Созылу өзектің көлденең өлшемінің қысқаруына алып келеді. Тәжірибеге сүйенсек, қысқару созушы кернеулікке пропорционал, яғни

d = -Pd₀ немесе d = d (1-p), (10.2)

мұндағы: d және d -өзектің созылғаннан кейінгі және бастапқы диаметрі; Р- материалдың көлденең қысылу коэффициенті; P - бір шамасымен салыстырғанда өте аз, өлшем бірлігі жоқ.

Материалдың көлденең қысылу коэффициентінің сызықтық созылу коэффициентіне қатынасы Пуассон коэффициенті деп аталады, ол мына түрде жазылады:

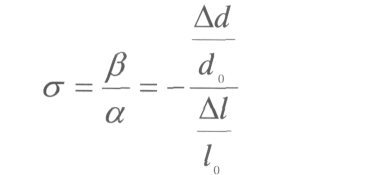
Есептеулер жүргізгенде Пуассон коэффициентінің тек тәжірибе жүзінде алынған - мәндері ғана қолданылады.

Ал кернеулік болса барлық жағдайда көлденең қимаға перпендикуляр бағытта емес, сондықтан оның мәні қиманың бағытына тәуелді. Өзектің ұшы көлбеу болсын. Ьұл жағдайда кернеулік:

P^I= = cos

Ал бұл кернеуліктің қимаға жанама және нормаль бағыттағы проекциясын қарастырсақ , онда олар былай анықталады:

P^, _t = P^I sin = cos sin

P _n = P^I cos = cos²

Р жанама кернеулік, кейде оны сыну кернеулігі дейді, сұйық пен газдарда бұл кернеулік болмайды, себебі онда қысым барлық бағытта бірдей таралады.

P_{n --} нормаль кернеулік, ол қатты денелерде және сұйықтарда таралады.