3 Тартылыс күшінің прекциясын анықтау

16 Билет

1 Серпінділік теориясының элементтері

Кез-келген дене сыртқы күш әсерінен деформацияға ұшырайды. Бұл кезде дененің жеке бөліктері бір-бірімен салыстырғанда ығысады. Ығысу шамасы дененің осы бөлігіндегі деформацияны сипаттайды.

Деформация кезінде қатты денелердің пішіні мен көлемі өзгереді, ал сұйықтардың - тек көлем ғана өзгереді, себебі олардың пішіні шектеуші ыдыстың немесе қабырғалардың пішініне тәуелді.

Сыртқы күш әсерін жойған кезде дененің алғашқы өлшемі жартылай немесе толық орнына келеді. Дененің қалпына қайта келуге ұмтылу қабілетін серпінділік қасиеті дейміз. Толық қалпына келген денені серпінді, жартылай қалпына келген денені - жартылай серпінді дейміз .

Табиғатта абсолютті серпінді дене жоқ, себебі деформация күші ұлғайған сайын деформация шегі байқалады, оның шамасы дененің физикалық қасиеттеріне байланысты. Сондықтан деформация шегіне жеткенше денені серпінді деп қарастыруға болады.

Дененің бетінің бірлік ауданына келетін сыртқы күш әсерін кернеулік дейміз. Сондықтан кернеулік - деформацияны сипаттайтын шама.

Сыртқы күштің уақыт бойынша өзгерісі бір мезгілде байқалмайды, себебі сыртқы күш әсері түсірілген нүктеден дененің басқа нүктелерге белгілі бір жылдамдықпен серпінді толқын түрінде келіп жетеді.

Сондықтан серпінділік теориясының негізгі мақсаіы деформацияны, кернеулікті, серпінді толқындарды сыртқы күш әсеріне байланысты анықтау.

2 Жазық электромагниттік толқын, оның кернеуліктерінің толқындық теңдеулері, шешімі

Максвелл теңдеулерінің негізінде электр өрісі айнымалы магнит өрісін, ал ол өріс қайтадан айнымалы электр ерісін тудыратынын байқадық. Олай болса, кеңістікте бұл өрістер өзіндік алмасулар арқылы толқын түрінде таралады. Бұл толқын тогы бар контурмен байланысқан немесе одан бөлінген түрінде кездесуі мүмкін. Сондықтан Максвелл теңдеулерін ерекше түрде жазылған толқындық теңдеулер деп есептеуге болады.

Толқындық теңдеулер - өрістің таралуын сипаттайтын қозғалыс теңдеуі. Ол өріс кернеуліктерінің кеңістікте координата және уақыт бойынша өзгерісін дифференциалды теңдеулер арқылы өрнектейді Бұл дифференциалды теңдеулер шешімі кернеуліктердің кеңістікте өзгеру заңдылықтарын береді. Олай болса, өрісті жеңіл зерттеуге мүмкіндік беретін толқындық теңдеулерді Максвеллдің негізгі екі теңдеуінен шығарамыз. Ол үшін Максвелл теңдеулерін бейтарап ортаға арнап жазамыз, яғни бұл шарт бойынша заряд тығыздығы р=0, өткізгіштік ток тығыздығы: . Егер кернеулік пен индукция арасындағы байланыстарды еске алсақ; . Онда бұл жағдай үшін Максвелл теңдеулер систетемасы;

rot ; div .

Максвеллдің негізгі екі теңдеуіне rot операциясын қолданамыз,

яғни теңдеудің екі жағынан да құйын аламыз:

rot ; div .

rot rot ,

rot rot .

rot белгісі функциядан координата бойынша алынған туындыны керсетеді. Олай болса теңдеудің оң жағындағы туынды алу кезегін езгертуге болады, онда бұл теңдеулер былай жазылады:

- ,

- (8.3)

Енді теңдеудің оң жағындағы rot rot шамалары (8.1) теңдеулер системасындағы өрнектермен алмастырылады, яғни :

;

.

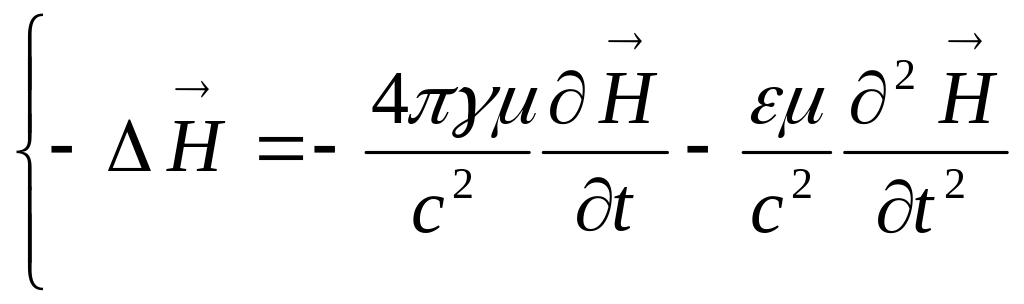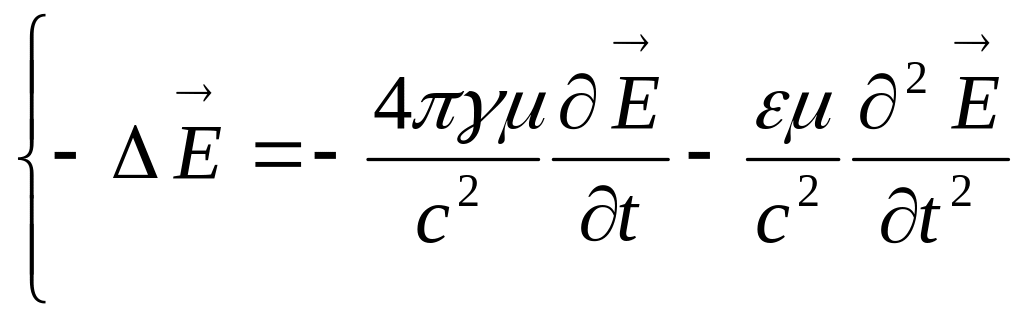Мұндағы -Лаплас операторы. Теңдеудің екі жағындағы теріс таңбаларды қысқартатын болсақ_э онда магниттік және электрлік кернеуліктердің таралуын сипаттайтын теңдеулерді аламыз, яғни :

;

.

Мұндай теңдеулер толқындық теңдеулер делінеді, немесе оларды телеграфтық теңдеулер деп те атайды.

- шамасын толқынның фазалық жылдамдығы деп атаймыз. Вакуумде , онда электромагниттік толқынның таралу жылдамдығы жарық жылдамдығына тең.

Егер өріс кернеуліктері уақыттан тәуелсіз болса, онда (8.4) теңдеулер системасы тұрақты токтың өрістеріне арналған Лаплас теңдеуін береді.

Гармоникалық электромагниттік өріс

Электробарлау жұмыстарында уақыт бойынша гармоникалық заңдылықтармен өзрегетін өрістердің маңызы зор. Мұндай өрістер әрі қарапайым, әрі зерттеуге өте жеңіл. Ондағы кернеуліктердің уақыт бойынша өзгерісі мынандай көбейткіш арқылы жазылады:

е^-iwt = cos wt – i sin wt;

Гармоникалық өрістегі кернеуліктерге арналған толқындық теңдеулерді жазу үшін оларды мына түрде өрнектеп:

е^{- iwt},

е^{- iwt}

уақыт бойынша туындыларын табамыз (электр өрісі кернеулігіне арнап жазамыз):

е ^{– iwt}) = е^{- iwt}

= ^-iwt=- ;

(8.5) теңдеулер системасындагы электр ерісі кернеулігіне арналған толқындық теңдеу былай жазылады:

+ немесе

,

онда электр және магнит өрісінің кернеуліктерінің толқындық теңдеуі былай жазылады:

, . (8.6)

Мұндағы: к - ортаның толқындық саны, ол мына коэффициенттермен анықталады:

к = = =

— ортаның сыну коэффициенті, — ортада жұтылу коэффициенті, олар комплексті санның түбірі ретінде анықталады:

n = ; ;

Егер ортаның электр өткізгіштігі {ү = 0) нольге тең болса, онда мұндай диэлектриктік ортада электромагниттік толқын сынады. Ал өткізгіштік ортада толқынның сыну да, жұлылуы да байқалады..

3