12Билет

1 Жай қабаттың логорифмдік тартылыс потенциалы

Цилиндрлiк бетте  тығыздығымен таралған массалардың тартылыс потенциалын анықтау үшiн, беттi енi d болатын жолақтарға бөлемiз. Оларды шексiз сызықтық дене ретiнде қарастырамыз, ондағы масса тығыздығы мына өрнекпен анықталады: =d , онда (13.3) өрнектiң негiзiнде потенциалды былай анықтаймыз:

. (13.5)

(13.5) - өрнек жазық жәй қабаттың логарифмдiк потенциалын анықтайды. Жалпы жағдайда -сызығы тұйық болмауы да мүмкiн. Бұл потенциал контурымен шектелген облыстың iшiнде де және сыртында да Лаплас теңдеуiн қанағаттандырады.

2Максвель тендеулерінің жүйесі

Бұл Максвелдің екі теңдеуіне индукция көзі анықтайтын электростатикалық екі теңдеуді топтастырсақ, онда кез-келген ортадағы электромагниттік өрісті сипаттайтын Максвелл теңдеулер системасын аламыз.

div = 4 , rot =

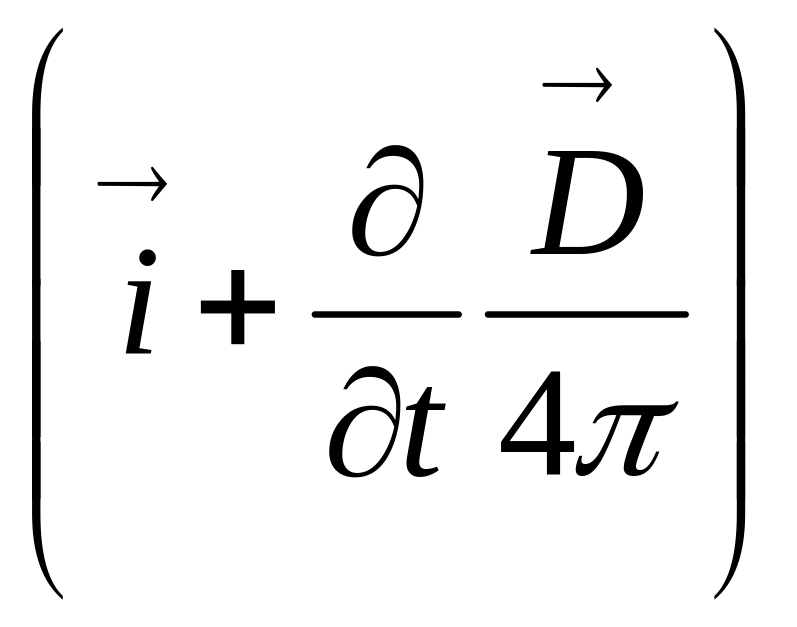
div = 0 , rot ;

Сонымен Максвелл тецдеулер системасы айнымалы өрістіц құйындарын анықтайды, яғни :

электр индукциясы өзгерген жерде құйынды магнит өрісі пайда болады, ал магнит индукциясы өзгерген жерде құйынды электр өрісі пайда болады.

Егер бұл системадағы өріс индукцияларының уақыт бойынша өзгерісі нольге тең болса, яғни :

=0 , =0,

онда тұрақты токтың электромагниттік өрісін сипаттайтын теңдеулер системасын аламыз, ол мына түрде жазылады:

rot = ; rot = 0 .

div = 0 ; div = 0.

3

13Билет

1Диполь логорифмдік потенциалы

Д

Сурет 2.

иполь мен қос қабат логарифмдiк потенциалы бар өрiсте - жазық өрiс құрайды. Жазық диполь - бiр-бiрiне жақын орналасқан, параллель екi сызық ретiнде қарастырылады. Олай болса, екi сызықтық массаның P нүктесiнде тудыратын потенциалы (13.3) теңдiк бойынша былай жазылады:

. (13.6)

Теңдiктiң (13.20) екi жағын да d көбейтiп, одан d 0 , шек алатын болсақ,

.

Мұнда – терiс таңбалы сызықтық массадан оң таңбалы сызықтық массаға бағытталған диполь моменті.

(13.7) –теңдiктi өзгертулер енгiзу арқылы диполь потенциалын былай жазуға болады:

, (13.8)

Мұндағы cos = cos(r,n) –нормаль мен радиус вектор арасындағы бұрыш.

2Электромагниттік өрістің кернеулігі, толқындық теңдеулері

Скин-эффект - беттік құбылыс, ол -өткізгіштің көлденең қимасы бойынша айнымалы токтың біркелкі тарала алмайтындығын көрсетеді. Ток тығыздығы өткізгіш бетінен ішкі қабатқа қарай азаяды. Максвелл теориясы бойынша бұл құбылыс - диэлектриктен өткізгішке түскен электромагниттік өрістің өткізгіштік ортада жұтылуымен түсіндіріледі. Яғни электромагниттік өрісті толқын түрінде таралады десек, ол өткізгіштік ортаға түскенде жарық толқыны тәрізді жұтылады. Айнымалы токтың жұтылуы электрлік барлау жүмыстарында өз эсерін тигізеді, оның шамасының азаюы Жердің төменгі қабатының әртектілігін ажыратуға мүмкіндік бермейді.

Скин- эффект қүбылысын қарастыру үшін қалыңдығы h болатын шексіз қабат аламыз.

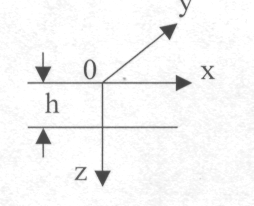
Координата басын оның бір қырына орналастырамыз. Онда ОХ бағыты бойынша электр өрісі, ал ОУ бағытымен магнит өрісі тербеледі. Олай болса, оларға перпендикуляр Z бағытымен гармоникалық электромагниттік өріс таралады. Мүндай өрістердің кернеуліктері мына заңдылықпен өзгереді:

,

( ) = .

Мұндағы гармоникалық өрістің кернеуліктері тригонометриялық заңдылықпен өзгереді. Кернеуліктерді анықтау үшін электромагниттік толқынның ОZ бағытымен таралуын еске ала отырып, кернеуліктің толқындық теңдеуінің жалпы түрдегі мына жазылымын пайдаланамыз:

(9.2)

Мұндағы k = - ортаның толқындық саны, ал n, ортаның сыну және жұтылу коэффициенттері.

(9.2)-теңдеу- қарапайым дифференциалдық теңдеулер, оның шешімдері мына түрде жазылады:

(9.3)

Бүл шешім- жалпы түрде жазылып тұр, оны нақты түрде алу үшін А₁ , А₂ , В₁, В₂-коэффициенттерін анықтауымыз қажет.Ол үшін мынандай шекаралық шарттар қолданамыз:

1) Электр өрісі өткізгіш қырларында бірдей таралады, яғни Е(0)=Е(Һ).

2)Магнит өрісінің шамасы бірдей болғанымен, бағыттары қарама - қарсы:

Н(0)= - Н(һ).

Бұл шартты (3) теңдікке қойсақ:

Мұнан: В₁=А₁е^ikh,, В₂ = - А₂е^ikh..

Онда нақты шешімді былай жазуға болады.

және коэффициенттері арасында да байланыс бар. Оны Максвеллдің екінші теңдеуінен аламыз:

Нақты шешімді тригонометриялық функция е ^–iwt арқылы және жоғарыда көрсетілген өзгерістерді қарастыра отырып, былай жазамыз:

(9.5)

немесе:

(9.6)

Бұл соңғы теңдеулер магнит жэне электр өрістерінің кернеуліктері екі толқын арқылы өрнектеліп тұрғандығын көрсетеді.Оның бірі - өткізгіш бетінен таралса, екіншісі - һ тереңдікте таралады.Толқын амплитудасы беттен тереңдеген сайын азая түседі, себебі амплитуда өзгерісі - жұтылу коэффициентіне теуелді экспоненциалды заңдылықпен анықталады.

Сондықтан, электромагниттік толқын өткізгіштік ортаға түскенде жұтылады, электр өрісі екі толқынның косындысымен , ал магнит өрісі -айырмасымен өрнектеледі.

Егер өткізгіш қимасының қалыңдығы шексіз десек, онда жазықтық орнына жартылай кеңістік аламыз. Бұл жағдайда жазықтықтың төменгі қырынан тарайтын толқын жойылады, себебі функцияның шексіз дәрежесі нольге айналады. Онда электр өрісінің кернеулігі былай анықталады:

. (9.7)

Бұл теңдеуді былай өзгертіп жазуға болады:

E (z,t) = .

Өріс амплитудасы көрсеткіштік заң бойынша кемиді: .

Толқын амплитудасы тереңдеген сайын азайып қана қоймай, белгілі тереңдікте өзінің фазасын өзгертеді, яғни өрістің бағыты өзгереді .Бұл жағдайда фазаны теңестірсек, өрістің бағыты өзгеретін тереңдікті былай анықтаймыз: z= ;

Диэлектриктер аралығында жазық толқынның шағылысуы мен сынуы.

Толқынды оның бетінің түрімен сипаттайды. Тербелістің нүктелік көзі біртекті ортада сфералық толқын тудырады. Айнымалы тогы бар тұйық тізбекті кеңістікте тербелістің нүктелік көзі ретінде қарастырсақ, одан тараған толқын сфералық болады. Сфераның ең кіші бөлігін жазықтық деп есептесек, одан таралатын толқынды – жазық толқын дейміз.

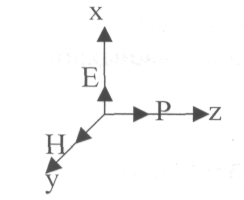
Тік бұрышты координаталар системасында жазық электромагниттік толқын ОZ-бағытымен таралсын, яғни толқын таралуы - уақыт жэне Z координатсына тәуелді.

ОХ-өсі бойынша электр өрісі , ОУ- өсі бойынша магнит өрісі бағытталған. Онда электромагниттік өрістің таралу бағытымен сәйкес келетін Умов-Пойнтинг векторы ОZ-өсімен бағытталып, бұл үш векторлар өзара перпендикуляр болады.

Электр өрісі тербелетін ХОZ-жазықтығы тербеліс жазьқтығы деп аталынады, ал магнит өрісі тербелетін ХОY жазықтығы-поляризация жазықтығы делінеді.

Электр жэне магнит өрісінің кернеуліктерінің толқындық теңдеулері мынандай түрде жазылады:

(9.8)

Бұл теңдеудің шешімдері мына түрде алынады:

; . (9.9)

Мұндағы ; вакуумде , онда .

Демек, электромагниттік толқынның жылдамдығы жарық жылдамдығына тең.Осыған байланысты Максвелл электромагниттік толқын мен жарық толқынының табиғаты бірдей деген тұжырымға келген.

Вакуум және ортадағы толқынның таралу жылдамдықтарының қатынасы сыну коэффициентін анықтайды. Диэлектриктер үшін бұл қатынас - Максвелл заңы деп аталынады:

Егер қарастырылып отырған толқын гармоникалық болса, онда (9.9) теңдеу шешімдері мына түрде жазылады:

; . (9.10)

Егер толқын ОZ'-бағыты бойынша таралса, онда бүл бағыт өстермен бұрышын жасайды. Онда (9.10) шешімге Z қашықтықтың орнына шамасы мынаған тең Z'қашықтығы қойылады: . Осыған байланысты кернеулік өрнектері былай жазылады.

Жазық толқын бір диэлектриктік ортадан екіншісіне жеткенде шағылысады және сынып екінші диэлектриктік ортаға өтеді. Максвелл теориясы арқылы оптикалық шағылысу жэне сыну заңдарын да анықтауға болады.

Ол үшін екі диэлектрик арасы жазық және олар біртекті деп саналады. ХОУ-координата жазықтығын шекарамен байланыстырамыз. Толқын бірінші диэлектриктен екіншіге координата өсьтерімен мынадай бұрыш жасап түседі: .;

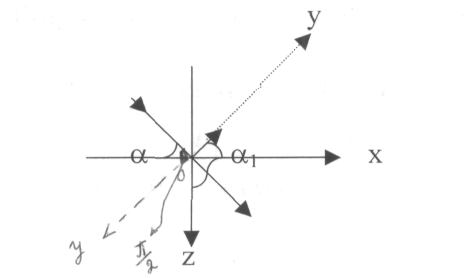
Шағылысқан толқын координата өсьтерімен мынадай бұрыштар жасайды: ; Сынған толқынға тән бұрыштар - .

Онда бұл толқындарға арналған кернеулік өрнектері былай жазылады:

1. Түскен толқын үшін:

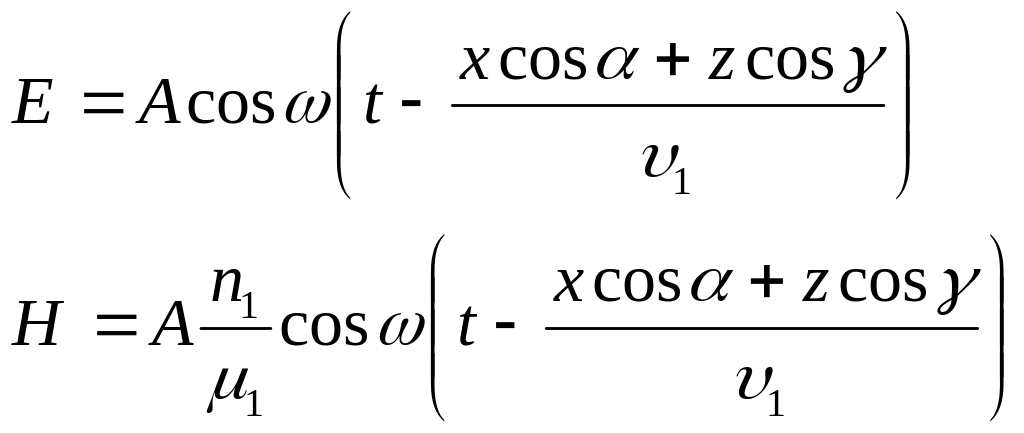
2. Шағылысқан толқын үшін:

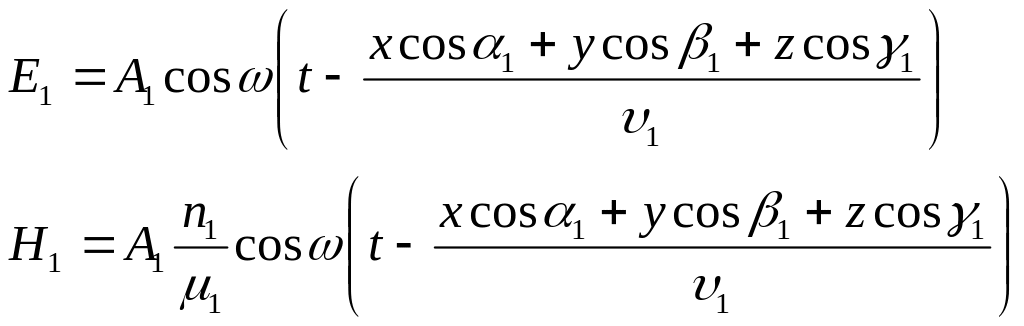
3. Сынған толқын үшін:

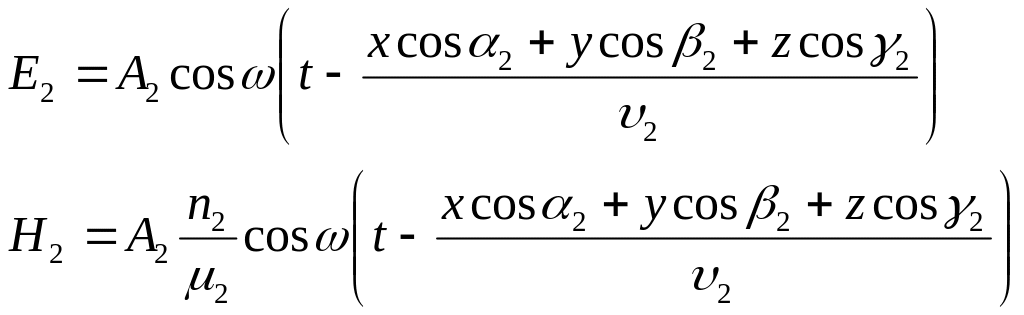
Z=0 жазықтығында, яғни толқынның түсу нүктесінде бұл үш толқынның фазасын кез-келген уақыт үшін бірдей болу керек, демек:

Егер х, у бір-біріне тәуелсіз десек, онда мынандай қатынас аламыз:

Бұл системадан мынандай теңдіктер шығады:

,

Сонымен, түсу бұрышын - , шағылу бұрышын - , ал сыну бұрышын - деп белгілесек, онда:

- толқынның түсу бұрышы мен шағылысу бұрышы өзара тең ;

- түсу және сыну бұрыштарының синустарының қатынасы түрақты шама, ол түскен жэне сынған толқын жылдамдықтарының қатынасына тең, яғни ;

- түскен, сынған жэне шағылысқан толқын бағыттары толқын түскен нүктеге тұрғызылған перпендикулярмен бір жазықтықта жатады.