11Билет

1 Сызықтық массаның логорифмдік тартылыс потенциалы

Бұл потенциал сызықтық масса потенциалы ретінде мына өрнекпен анықталады:

.

Т

Сурет 1.

ығыздығы тұрақты массалар жиынын - L сызығы бойымен Жер бетінен z₀ тереңдікте у осіне параллель орналасқан деп есептеп, оның бойындағы М(0,у,z₀) нүктесiнен ұзындығы d болатын элементар кесінді аламыз (сурет 1).

М –нүктесiнде алынған кесіндідегі массаның х-осiнде жатқан P(х,0,0) нүктесiндегі бірлік массаға әсер ететін тартылыс потенциалын қарастырамыз.

М нүктесiнен P нүктесiне дейiнгi арақашықтық r –радиус вектор арқылы анықталады, ол мынаған тең:

Сурет 1. .

М асса таралған сызықтың ұзындығы L=2 тең болған жағдайда, оның тудыратын тартылыс потенциалын [- , ] шекарасында анықтаймыз. Онда (1) интегралдық өрнек былай жазылады:

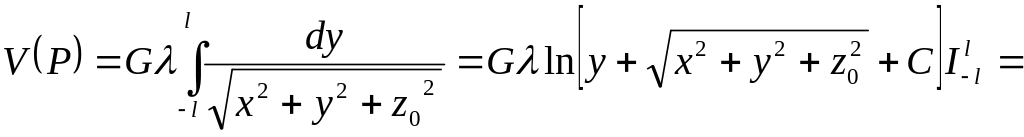
(13.1)

Бұл (1) өрнек арқылы ұзындығы 2 түзу сызық бойындағы массаның P нүктесiнде тудыратын потенциалын анықтауға болады.

Мынандай жағдайды қарастырамыз:

, (13.2)

яғни масса таралған сызықтың ұзындығы өте үлкен болғанда түбiрдi жуық шамамен алуға болады:

.

Онда (1) өрнек былай жазылады:

.

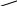
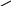
Егер (13.2) шартты ескерсек, бөлшектің алымындағы ( ) қосындыны еске алмауға болады, онда бұл потенциал былай жазылады:

.

Мұны екi логарифмге жiктеймiз :

.

Егер сызықтық өлшем  шексiз үлкен болса, онда ln (2 ), және ол тұрақты. Практикада потенциалдың абсолюттiк шамасы емес, оның екі нүкте арасындағы айырмасының және градиентiнiң шамасының практикалық мәнi жоғары. Осыған байланысты тұрақты шамамен анықталатын потенциал бөлігін еске алмауға болады. Сондықтан z тереңдiкте жатқан шексiз бiртектi сызықтық дене тудыратын тартылыс потенциалы мына өрнекпен анықталады:

. 13.3)

Бұл логарифмдiк потенциал, ол - сызықтық дене таралған бағытқа тәуелсiз.

Логарифмдік потенциал тартылыс потенциалына тән барлық қасиетке ие болады, ал бұл потенциалдың шексіздікте теріс таңбалы шексіздікке айналатыны – оның тартылыс потенциалынан айырмашылығы болып табылады.

Соңғы өрнектен (13.3) тартылыс күштерінің проекцияларын табамыз:

, ,

ал тартылыс күші векторлық түрде былай жазылады:

2 Максвельдің екінші тендеуі

Ол дифференциалды түрде жазылған индукция заңы болып саналады. Заң бойынша контурда пайда болған э.қ.к. магнит индукциясының ағынының бірлік уақыттағы өзгерісіне тең, теріс таңбамен алынған, яғни:

. (7.9)

Ал Максвелл болса, э.қ.к. пайда болуын уақыт бойынша өзгермелі магнит өрісінде құйынды электр өрісінің тууымен түсіндіреді. Құйынды өрістің күш сызықтары өзімен өзі тұйықталғанда магнит индукциясы векторының өзгермелі ағынын қамтиды. Осыған байланысты индукция э.қ.к. -құйынды өрістің циркуляциясымен алмастырылады, яғни:

Магнит ағыны- магнит индукциясынан бет бойынша интегралмен алмастырылады, яғни:

Ф = .

Осы алмастыруды орындасақ, онда индукция заңын Максвелл түсінігі бойынша аламыз:

. (7.10)

(10) теңдіктің сол жағын Стокс теоромасы бойынша беттік интегралға айналдырамыз. Онда (10) теңдік былай жазылады:

ds = -

Бұл теңдік кез-келген өлшемдегі бет үшін орындалады, егер интеграл астындағы шамалар өзара тең болса, яғни:

rot_n = - ;

яғни кез-келген нормаль бағыты үшін де бұл екі вектор өзара тең, яғни:

rot = - ; (7.11)

(7.11) өрнек индукция заңының дифференциалдық жазылымы, немесе Максвеллдіц екінші тецдеуі.

Бүл теңдеудің физикалық мағнасы:

электр өрісін тек зарядтар ғана тудырмайды, уақыт бойынша өзгермелі магнит өрісі де тудырады.

- -шамасын магниттік ығысу тогы деп айтуға болады, ол пайда болғанда оның айналасында электр өрісі туады. (-) теріс таңба магниттік ығысу тогы магнит индукциясы уақыт бойынша азайғанда оң болатынын көрсетеді. Бұл ток пайда болған жерде айнымалы электр өрісі пайда болады.

3