1

Срет 3.

) Р нүктесі облысының ішінде жатқан жағдайда да көлемдік массаның тартылыс потенциалы ешқашан шексіздікке айналмайды. 2) Бірлік массасы бар Р нүктесі тартылыс тудыратын массадан тысқары орналасқан жағдайда көлемдік массаның тартылыс потенциалы Лаплас теңдеуін қанағаттандырады:

0,

3) Р нүктесі облысының ішінде жатқан жағдайда көлемдік массаның тартылыс потенциалы Пуассон теңдеуін қанағаттандырады:

- 4G.

4. Көлемдік массаның сызықтық өлшемдері Р нүктесіне дейінгі арақашықтықпен салыстырғанда әлдеқайда төмен болса, онда оның тартылысы нүктелік массаның тартылысындай болады.

5. Тартылыс потенциалы өзінің ең жоғарғы және төменгі мәндеріне массалар таралған облысын шектейтін бетте ие болады.

Көлемдік массаның тартылыс күшін тартылыс потенциалы арқылы өрнектейміз, ол үшін алдымен күш проекциялары жазамыз:

. , , ,

онда тартылыс күшінің векторлық жазылымы мынандай түрге ие болады: .

Жәй қабаттың тартылыс потенциалы

С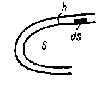 урет 4.

Тартылыс тудыратын массалар S жазығының бетінде h қалыңдығы бар қабат ретінде кездеседі. (сурет 4). Егер қабат қалыңдығын жазық беттің басқа екі сызықтық өлшемімен саыстырғанда еске алмауға болатындай болса, онда массаны жазық бет бойынша таралған деп есептеуге болады.

Жазық беттегі массаның таралу тығыздығы - тең десек, онда элементар бетке сәйкес келетін массаның таралымы: , онда жәй қабаттың тартылыс потенциалы мына өрнекпен анықталады:

. (12.6)

Бұл функция S бетінде жатпайтын кез келген нүкте үшін ақырғы мәнге ие болады, үздіксіз, біржақты координатадан тәуелді функция, оның кез келген дәрежедегі жеке туындылары бар.

Жәй қабаттың тартылыс күші мен оның проекциялары потенциал арқылы былай жазылады:

. , , ,

Б

Сурет 5.

ұл өрнек гравибарлауда түрлі жазық денелердің тудыратын ауырлық күшін есептеуге кеңінен қолданылады.

Сызықтық массалардың тартылыс потенциалы

Сурет 5.

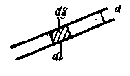
Егер екі бағыттағы өлшемін үшінші бағыттағы өлшеміне қарағанда еске алмауға болатын денелерді - сызық бойымен таралған масса ретінде қарастыруға болады (Сурет 5). Сызық бойындағы массаның таралу тығыздығын

десек, онда элементар сызықтық масса мына

өрнекпен анықталады: , ал бүкіл сызық бойымен орналасқан массалардың тудыратын тартылыс потенциалын былай есептейміз:

. (12.7)

Бұл потенциал арқылы сызықтық массаның тартылыс күшін өрнектеуге болады, алдымен күш проекцияларын қарастырамыз:

, , ,

онда сызықтық масса тартылыс күші векторлық түрде былай жазылады:

Магниттiк масса

Магниттiк масса көзi ретiнде магниттелген дененi қарастырамыз. Бiр-бiрiнен белгілі қашықтықта орналасқан m₁, m₂ екi магниттiк массаның немесе зарядталған екі дененің өзара әсерi Кулон заңымен анықталады, яғни екi масса арасындағы әсер ету күші мына өрнекпен жазылады:

r- екi нүкте арасының қашықтығы, -ортаның диэлектриктiк өткiзгiштiгi.

Егер m₁ = m тең, ал m₂= 1 десек, олар М(х₀, у₀, z₀) және P(x,y,z) нүктесiнде орналасқан болса, онда 1 болғанда Кулон заңы былай жазылады:

(12.8)

Бiрлiк массаға әсер ететiн бұл күш өрiстiң кернеулiгiн сипаттайды.

Гравитациялық массаға қарағанда магниттiк массалар бiр таңбалы болмайды. Кез-келген оң таңбалы массаға шамасы сондай терiс таңбалы масса сәйкес келедi. Егер магниттiң бiр полюсi шексiздiкте десек, сонда ғана бiр таңбалы магниттiк масса туралы айтуға болады.

Бұл дененiң магнит өрiсiн элементар дипольдiң өрiстерiнiң қосындысы ретiнде анықтаймыз.

Диполь потенциалы

С

Сурет 1.

урет 6.

Диполь өрісін жеке қарастырамыз (Сурет 6). Шамасы бірдей, бірақ таңбалары қарама-қарсы m және -m массаларды М₁ , М₂ нүктелеріне орналастырамыз, мұндағы:

- оң полюстегі m -нүктелiк көздiң қуаты;

- екi полюс арақашықтығы d –диполь ұзындығы;

- екі полюсті қосатын түзу сызық - диполь өсі, ол терiс массадан оң массаға бағытталған вектор, оның бойымен алынған бірлік вектор деп белгіленеді ;

- диполь өсін тең бөлетiн М нүктесi - диполь центрi;

- диполь өсіне перпендикуляр, М нүктесі арқылы өтетін жазықтық – экваториалды жазықтық.

Бұл массалардың P нүктесiнде тудыратын потенциалын қарастырамыз. r₁, r₂ – P нүктесiнен терiс және оң масса орналасқан М₂, М₁-нүктесiне дейiнгi қашықтық, М нүктесiне дейiнгi арақашықтығы r,

Мұндай екі нүктелік массалар тудыратын Р нүктесіндегі тартылыс потенциалы – нүктелік массалар системасының потенциалы ретінде анықталады :

. (12.9)

(9)теңдiктiң оң жағын d -көбейтiп, бөлсек мынандай өрнек аламыз;

, (12.10)

бұл өрнектегi жақша ішіндегі шама функциясының бағыты бойынша ұмтылғандағы туындысы деп қарастыруға болады, яғни:

Егер бұл туындыны былай түрлендiрсек:

,

мұндағы:  - r және бағыттары арасындағы бұрыш.

Егер - диполь моментіне тең десек, онда (12.10) теңдеу былай жазылады:

. (12.11)

Бұл потенциал ара қашықтық квадратына керi пропорционал, әрi радиус вектордың диполь моментi бағытынан ауытқу бұрышына тәуелдi.

Магниттелген көлемдiк дененiң потенциалы

Бiртұтас магниттелген дененi - магниттiк өстерi реттелiп орналасқан диполь ретiнде қарастырамыз. Элементар көлемге сәйкес магниттiк моменттi мына өрнекпен анықтаймыз: d= jdV, мұндағы j- магниттелу векторы.

Егер әрбiр көлем элементiн, яғни элементар көлемдi диполь деп қарастырсақ, онда оның тудыратын потенциалы былай жазылады:

Егер бұл өрнектi көлем бойынша интегралдайтын болсақ, онда магниттелген көлемдiк массаның P нүктесiнде тудыратын потенциалын анықтаймыз:

. (12.12)

Қ ос қабаттың тартылыс потенциалы

Гравитациялық массалар оң және терiс таңбамен қарастырылатын болса, онда қос қабат деген ұғым енгіземіз.

S-қабаты берiлсiн, оның екi жағынан бiрдей қашықтықта бетке нормаль бағыт бойынша S₁ және S₂ қабатын қарастырамыз. Бұл қабаттардан бiр түзу сызық бойында жататын М₁ , М , М₂ –нүктелерiн белгiлеймiз (Сурет 7).

М₁ М₂- нүктелерінің арақашықтығын d деп белгiлеймiз, ол М нүктесi арқылы тең екi бөлiкке бөлiнген. S₂, S₁ беттерiнде жатқан Сурет 7. бұл нүктелердегi массаның беттiк тығыздығы - . Массалардың беттердегі мұндай таралымы - олардың арасындағы қашықтық нольге ұмтылғанда ( ) қос қабат құрайды.

Демек, бiр түзудiң бойындағы шамасы бiрдей, таңбасы қарама-қарсы беттiк массалар тығыздығы қос қабат делiнедi.

Мұнда беттiк массалар орналасқан нүктелердiң арақашықтығы – d - қос қабаттың қалыңдығы деп аталынады.

Бұл массалардың осы беттерден тысқары жатқан P нүктесiнде тудыратын потенциалын анықтаймыз. Ол үшiн алдымен М₁, М₂- нүктесiндегi массаларды өрнектеймiз. Бұл нүктелер элементар dS₁ , dS₂ беттеріне сәйкес келсе, онда нүктедегi элементар массалар мына өрнекпен анықталады:

dm₁= dS₁ , dm₂= - dS₂,

Егер dS₁ және dS₂ беттерін – dS –бетiнiң проекциясы ретінде қарастырсақ, онда бұл өрнек былай жазылады:

dm₁= dS , dm₂= -dS ,

Бұл жағдайда қос қабаттың элментар диполь ретiнде қарастыруға болады.

Ал диполь моменті бұл жағдайда былай анықталады:

= dS,

мұндағы -қос қабат тығыздығы, оны кейде қос қабаттың моментi немесе қуаты дейдi.

Қарастырылып отырған қос қабат потенциалын элементар бетке арналған dV деп белгiлесек, ол  орнына dS-өрнегiн қойғанда, G- шамасына көбейтiлген диполь потенциалымен анықталады:

Бұл өрнектiң екi жағын интегралдасақ, онда қос қабаттың тартылыс потенциалын аламыз.

. (12.13)

2ығысу тоғы

Жаңа теория ғылымға жаңа ұғым алып келеді. Максвелл теориясының жаңа үғымы- ыгысу тогы болып саналады. Бұл ұғымға толық түсінік беру үшін конденсатор жалғанған айнымалы ток тізбегін қарастырамыз.

Токты зарядтардың реттелген қозғалысы ретінде қарастыра отырып, контурдағы ток конденсатор жиегіне келгенде үзіліп қалады деп есептеуге болады. Осыған байланысты Кирхгофтың бірінші заңы орындалмайды. Ал Максвелл теориясы бойынша ток үзілмейді, ол зарядтардың реттелген қозғалысы арқылы емес, ыгысу тогы арқылы жалғасады.

Ыгысу тогы деп конденсатордың қабаттар арасындағы электр өрісінің уақыт бойынша өзгерісін айтамыз.

Егер конденсатор қабаттарындағы заряд шамасы өзгерсе, онда қатпарлар арасында электр өрісінің уақыт бойынша өзгерісі пайда болады. Мұндай жағдайда өткізгіштегі жаңа ток шамасын конденсатор қатпарындағы зарядтардың уакыт бойынша өзгерісімен сипаттаймыз.

(7.1)

Мүндағы : Q-заряд, электростатикалық заңдылық бойынша қатпардағы заряд шамасы мына өрнепен анықталады:

мүндағы: S-қатпар ауданы, D-электр индукциясы. Олай болса (7.1) теңдеу былай жазылады:

. (7.2)

Токты анықтауда зарядтан (Q ) электрлік индукцияға (D) көшудің физикалық мэні бар: мұнда ток конденсатор қатпар арасындағы электр өрісінің уақыт бойынша өзгерісімен сипатталып тұр, себебі : ; олай болса (7.2) теңдеу конденсаторға арналған Кирхгофтың I заңын береді.

(7.2) теңдеудің сол жағын да конденсаторға ағып келген ток( ) тұр, Максвелл теориясы бойынша бұл- өткізгіштік ток, ал оң жағында конденсатор қатпары арасындағы диэлектрик бойынша ағып өтетін ығысу тогы тұр. Мұндағы: -электрлік ығысу векторы деп аталынады, ал оның уақыт бойынша туындысы - ығысу тогының тығыздығын береді;

Демек, ток ұғымы туралы жалпы қортынды, айнымалы ток үшін Био-Савар заңын да дифференциалды түрде жазуға мүмкіндік береді.