
Статистические характеристики пространственно-временной изменчивости направления ветра в приземном слое.
ВСТУПЛЕНИЕ
Земная атмосфера представляет собой неоднородную среду, в которой скорость ветра, температура, влажность и другие гидродинамические и термодинамические величины являются функциями от координат и от времени.
Наряду с плавными изменениями этих величин, характеризующими зависимость от времени и координат средних метеорологических условий, в реальной атмосфере наблюдаются также беспорядочные флуктуации, обусловленные турбулентностью. Наличие этих турбулентных флуктуаций приводит, в частности, к тому, что перемешивание атмосферы, т.е. обмен воздушных масс теплом, влагой, примесями, количеством движения, ускоряется во много тысяч раз. Помимо того, турбулентность играет важную роль и в ряде других физических процессов, протекающих в атмосфере.
Так как мелкомасштабные пульсации температуры и скорости ветра носят случайный характер, для их описания была развита теория стационарных случайных процессов. [1]. Позднее была создана полуэмпирическая теория приземного слоя[2], которая также целиком опирается на статистическое описание. Это означает, что в ней не предполагается рассмотрение присутствие организованных (когерентных) структур. Развитие методов наблюдения позволило с очевидностью показать, что структуры существуют и именно они ответственны за основную часть переноса импульса, тепла и примесей. Поэтому исследование структур в случайных полях скорости и температуры в приземном слое атмосферы в настоящее время сочетается со статистическим подходом, ставившим своей главной целью изучение осредненных зависимостей статистических характеристик течений от координат в стационарных условиях. Отметим также, что большинство экспериментальных работ основывается лишь на данных одноточечных измерений. Многоточечные же измерения, могут дать много полезной информации, как в рамках статистического описания, так и в особенности в плане обнаружения когерентных структур. Поэтому, хотя многоточечные измерения оказываются очень затратными и трудоемкими, они все более широко применяются на практике. Бурное развитие систем регистрации данных и вычислительных мощностей позволяет справиться с огромными объемами получаемой в ходе эксперимента информации. Настоящее исследование посвящено исследованию пространственно-временной изменчивости направления ветра в приземном слое атмосферы.
Качественное описание турбулентности
Современные познания в области законов турбулентных течений в значительной степени базируются на идеях и результатах, содержащихся в нескольких небольших статьях, опубликованных по этому вопросу в 1941 г. Андреем Николаевичем Колмогоровым. Эти статьи явились фундаментальным вкладом в теорию турбулентности, начатую еще классическими работами Рейнольдса 1883 и 1894 гг.
Рейнольдс основное внимание уделил условиям, при которых ламинарное течение в трубах превращается в турбулентное течение. При этом он установил общий критерий динамического подобия двух геометрически подобных течений вязкой несжимаемой жидкости в отсутствие внешних сил: таким критерием является совпадение у этих течений значений так называемого числа Рейнольдса
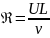 , (1)
, (1)
где
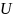 и
и
 – характерные масштабы скорости и длины
в рассматриваемых течениях, а
– характерные масштабы скорости и длины
в рассматриваемых течениях, а
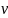 – кинематический коэффициент вязкости
жидкости. С динамической точки зрения
число
– кинематический коэффициент вязкости
жидкости. С динамической точки зрения
число
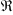 может быть интерпретировано как отношение
типичных значений сил инерции и сил
вязкости, действующих внутри жидкости.
Силы инерции, вызывающие перемешивание
отдельных объемов жидкости, движущихся
«по инерции» с разными скоростями,
осуществляют передачу энергии от
крупномасштабных компонент движения
к мелкомасштабным и тем самым способствуют
образованию в потоке резких (мелкомасштабных)
неоднородностей, характерных для
турбулентного режима; силы вязкости,
наоборот, приводят к сглаживанию
мелкомасштабных неоднородностей.
Поэтому следует ожидать, что течения с
достаточно малыми значениями
будут ламинарными, а течения с достаточно
большим
– турбулентными. Этот основной результат
был четко сформулирован Рейнольдсом.
может быть интерпретировано как отношение
типичных значений сил инерции и сил
вязкости, действующих внутри жидкости.
Силы инерции, вызывающие перемешивание
отдельных объемов жидкости, движущихся
«по инерции» с разными скоростями,
осуществляют передачу энергии от
крупномасштабных компонент движения
к мелкомасштабным и тем самым способствуют
образованию в потоке резких (мелкомасштабных)
неоднородностей, характерных для
турбулентного режима; силы вязкости,
наоборот, приводят к сглаживанию
мелкомасштабных неоднородностей.
Поэтому следует ожидать, что течения с
достаточно малыми значениями
будут ламинарными, а течения с достаточно
большим
– турбулентными. Этот основной результат
был четко сформулирован Рейнольдсом.
Еще
в 20-х годах 20-го века английский ученый
Л. Ричардсон, отметил, что развитая
турбулентность должна представлять
собой иерархию «вихрей» (т.е. возмущений
или неоднородностей) разных порядков,
отличающихся характерными масштабами
и скоростями. Самые крупные из этих
возмущений – возмущения первого порядка,
характеризующиеся масштабом длины
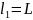 (сравнимым с типичным масштабом всего
течения в целом) и масштабом скорости
(сравнимым с типичным масштабом всего
течения в целом) и масштабом скорости
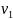 (по порядку величины сравнимым с
изменением средней скорости
на расстояниях порядка
(по порядку величины сравнимым с
изменением средней скорости
на расстояниях порядка
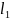 ),
заимствуют свою энергию непосредственно
из осредненного движения и возникают
из-за неустойчивости этого движения
при достаточно большом
.
Но при очень большом
число Рейнольдса
),
заимствуют свою энергию непосредственно
из осредненного движения и возникают
из-за неустойчивости этого движения
при достаточно большом
.
Но при очень большом
число Рейнольдса
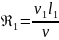 «неоднородностей первого порядка»
также будет велико; поэтому эти наиболее
крупномасштабные возмущения в свою
очередь будут являться неустойчивыми
и, распадаясь, будут порождать «турбулентные
возмущения второго порядка» (масштаба
«неоднородностей первого порядка»
также будет велико; поэтому эти наиболее
крупномасштабные возмущения в свою
очередь будут являться неустойчивыми
и, распадаясь, будут порождать «турбулентные
возмущения второго порядка» (масштаба
 и с характерной скоростью
и с характерной скоростью
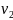 ),
передавая им часть
своей энергии. Число Рейнольдса
),
передавая им часть
своей энергии. Число Рейнольдса
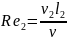 «вторичных» возмущений меньше чем
«вторичных» возмущений меньше чем
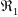 ,
но и оно при достаточно большом
будет столь велико, что отвечающие ему
движения также будут неустойчивыми и
будут распадаться на «возмущения
третьего порядка» еще меньшего масштаба
,
но и оно при достаточно большом
будет столь велико, что отвечающие ему
движения также будут неустойчивыми и
будут распадаться на «возмущения
третьего порядка» еще меньшего масштаба
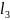 и с еще меньшей
скоростью
и с еще меньшей
скоростью
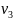 и т.д. Таким образом возникает своеобразный
«каскадный процесс», при котором энергия
крупномасштабных движений последовательно
передается все меньшим и меньшим
движениям вплоть до движений некоторого
минимального масштаба
и т.д. Таким образом возникает своеобразный
«каскадный процесс», при котором энергия
крупномасштабных движений последовательно
передается все меньшим и меньшим
движениям вплоть до движений некоторого
минимального масштаба
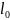 ,
таких, что отвечающее им число Рейнольдса
уже характеризует устойчивое ламинарное
движение. Малость числа Рейнолдса для
движений масштаба
означает, что в этих движениях вязкость
играет существенную роль, т. е. что в них
происходит заметный переход кинетической
энергии, затрачиваемой на преодоление
силы трения, в тепло (диссипация
кинетической энергии). Что же касается
движений с масштабами
,
таких, что отвечающее им число Рейнольдса
уже характеризует устойчивое ламинарное
движение. Малость числа Рейнолдса для
движений масштаба
означает, что в этих движениях вязкость
играет существенную роль, т. е. что в них
происходит заметный переход кинетической
энергии, затрачиваемой на преодоление
силы трения, в тепло (диссипация
кинетической энергии). Что же касается
движений с масштабами
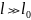 ,
то для них вязкость не играет большой
роли и, значит, в них не происходит
заметной диссипации энергии.
,
то для них вязкость не играет большой
роли и, значит, в них не происходит
заметной диссипации энергии.
Факт перехода энергии в турбулентном потоке из области малых частот спектра в область больших частот может быть объяснен нелинейностью уравнений гидромеханики; в линейной колебательной системе обмена энергии между различными частотами не происходит. Рейнольдс первый указал на нелинейность уравнений гидромеханики как на причину трансформации энергии в турбулентном потоке.
