Швидкість фільтрації.
Під швидкістю фільтрації розуміють витрату рідини, тобто, обсяг рідини, що протікає в одиницю часу через одиницю площі , виділену в пористої середовищі . Згадаймо , як визначається витрата рідини в гідродинаміці ( Кочин , Кибель і Розі 1963 , 1 ) . Нехай є елементарний майданчик S (рис. 10 ), через яку проходить рідина зі швидкістю , що представляється вектором і . Кількість рідини ,
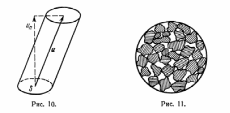
протікає
в одиницю часу через S , дорівнює обсягу
циліндра , побудованого на S, а оскільки
висота цього циліндра дорівнює – нормлі
до
майданчика S складової швидкості , то
витрата Q через майданчик S дорівнює Q =
S
.
Якщо в даній точці обертати елементарну
площадку і відновлювати нормалі до неї
, той напрямок я , відповідне найбільшому
витраті , буде напрямком вектора
швидкості. Звернемося
до руху рідини в пористому середовищі
. Уявімо собі майданчик в грунті , що
містить перетину зерен грунту і просвіти
між цими перетинами (рис. 11 ) . Рух рідини
між зернами грунту носить складний
характер , тому прийнято розглядати не
швидкості в окремих точках рідини , а
середні значення цих швидкостей.
Нехай вектор середньої швидкості частинок рідини в області майданчики S буде і . Площу, що знаходяться на майданчику S , позначимо через S1. Покладемо
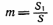
і назвемо m поверхневою пористістю. Витрата через майданчик S буде
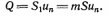
Витрата через майданчик, величина якої дорівнює одиниці, дорівнює і називається швидкістю фільтрації. Вектор швидкості фільтрації має величину рівну максимальному значенню при різних положеннях майданчика S, і спрямований по нормалі до того майданчику, через який проходить найбільша витрата.
Якщо
вектор швидкості частки має складові
то для вектора швидкості фільтрації V
складові
Для того щоб визначити поверхневу пористість деякого зразка , можна було б вчинити так , як це роблять у деяких спеціальних лабораторіях : зразок , вийнятий з грунту за допомогою циліндричної трубки з гострими краями ( такий зразок називають керном ) , просочують клейкою речовиною і потім роблять ряд тонких зрізів цього зразка . Поклавши зрізи під мікроскоп , можна виміряти площі просвітів і взяти їх співідношення до площі перетину зразка. Середнє з цих величин по всіх узятим перетинах дає середню поверхневу пористість взятого зразка. Однак такий спосіб її визначення складний. Разом з тим очевидно , що описаний прийом визначення поверхневої пористості дасть для нашого циліндричного зразка величину середньої пористості грунту .
Справді
, припускаючи , що середовище статистично
однорідне , позначимо через площу
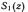отворів в перетині циліндра на відстані
z
від його основи (рис. 12 ) .
Нехай m (z) буде просвітні цього перерізу, т. е.
де S-площа основи циліндра. Тоді середнє значення просвітні m дорівнюватиме
Це вираз можна представити так:
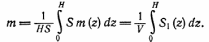
Тут HS = V - об'єм аналізованого циліндра, а інтеграл дорівнює обсягу V1 всіх пір в даному зразку. Тому середня просвітні або поверхнева пористість m дорівнює середній об'ємнsq пористості а: