
- •1. Расчет коэффициента усиления сау
- •2.Расчет и построение внешних статических характеристик сау
- •3. Определение передаточной функции исходной сау, расчет корней характеристического уравнения
- •4.Расчет и построение частотных характеристик эквивалентной разомкнутой сау: афчх, лачх, лфчх. Определение устойчивости по частотным характеристикам.
- •5.Проверка на устойчивость исходной сау по критерию Гурвица
- •6. Моделирование переходных характеристик исходной сау
- •1.) При отсутствии возмущений для граничных значений g.
- •7.Синтез корректирующего устройства, обеспечивающего настройку исходной системы на симметричный оптимум.
- •7.1. Синтез регулятора упрощённой сау, обеспечивающей настройку исходной системы на симметричный оптимум.
- •8. Моделирование переходных характеристик сау, скорректированной на симметричный оптимум.
- •8.1. Моделирование переходных характеристик упрощённой сау, скорректированной на симметричный оптимум.
- •8.2. Моделирование переходных характеристик упрощённой сау, скорректированной на симметричный оптимум(объект управления упрощён).
- •Заключение
- •Список используемой литературы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «ЭРЭиЭС»
Пояснительная записка к курсовой работе по дисциплине
«Теория автоматического управления»
БГТУ. ТАУКП. 05 . 000 ПЗ
Руководитель:
Хвостов В.А.
«____»___________
Выполнил студент группы 11 ЭиН-1
Жук В.А.
«____»___________
БРЯНСК 2013
Содержание
1. Расчет коэффициента усиления САУ……………………………………….4
2. Расчет и построение внешних статических характеристик……………….5
3. Определение передаточной функции исходной САУ, расчёт корней характеристического уравнения……………………………………………..6
4. Расчет и построение частотных характеристик эквивалентной
разомкнутой САУ: АФЧХ, ЛАЧХ и ЛФЧХ……………………………………7
5. Проверка на устойчивость исходной САУ по критерию Гурвица………...10
6. Моделирование переходных характеристик исходной САУ………………11
1. Расчет коэффициента усиления сау
Расчет коэффициента усиления регулятора (K), обеспечивающего статическую ошибку не более 2.8% при изменении задания (g) и возмущения (z) в указанных диапазонах.
Расчет коэффициента усиления производится в статическом режиме, когда p=0. Структурная схема САУ в статическом режиме представлена на рис.1.
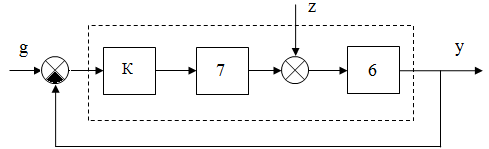
Рисунок 1. Структурная схема САУ
Статическая ошибка:

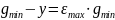
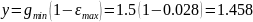
Запишем уравнение для данной САУ на основе ее структурной схемы:
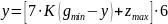




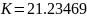
2.Расчет и построение внешних статических характеристик сау
Имея представление о статических характеристиках элементов и зная их взаимосвязь внутри САУ, можно получить представление о САУ в целом.
Внешняя
статическая характеристика САУ – это
зависимость выходного сигнала
 от контролируемых возмущений z.
от контролируемых возмущений z.
Запишем уравнение для данной САУ на основе ее структурной схемы:

При gmin=1.5
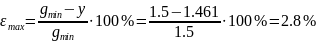
-
Z
0
-6
Y
1.497
1.458

При g=5
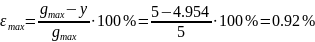
Z |
0 |
-6 |
Y |
4.99 |
4.954 |
При gmax=12

-
Z
0
-6
Y
11.976
11.94
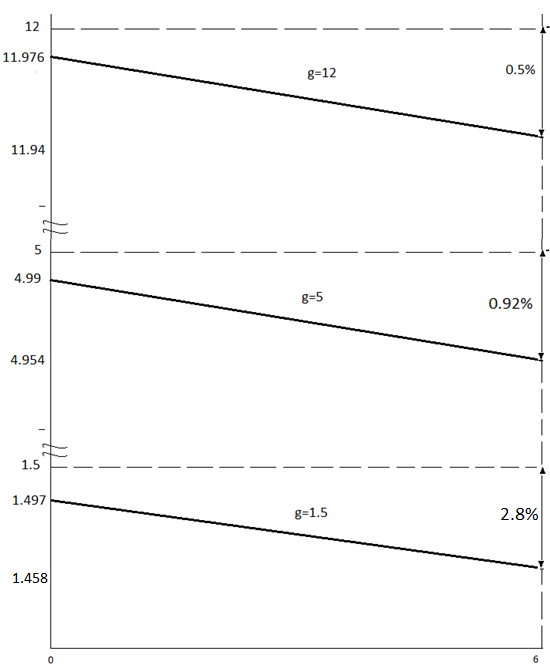
 Рисунок
2. Внешние статические харатеристики.
Рисунок
2. Внешние статические харатеристики.
3. Определение передаточной функции исходной сау, расчет корней характеристического уравнения
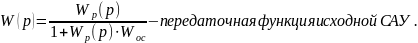

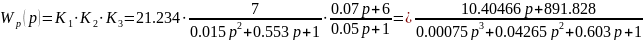
Так
как обратная связь единична, то
 ,
значит
,
значит

Знаменатель
передаточной функции - это характеристический
полином системы:

К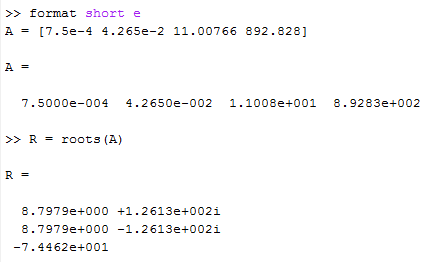 орни
этого полинома определяют вид и параметры
переходной характеристики САУ. Решая
кубическое уравнение в среде Matlab,
получаем корни:
орни
этого полинома определяют вид и параметры
переходной характеристики САУ. Решая
кубическое уравнение в среде Matlab,
получаем корни:

Рисунок 3. Вычисление корней характеристического уравнения в Matlab.
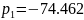

Таким образом, по корням характеристического уравнения мы можем предположить, что система не устойчива.
Т.к.
вещественная часть (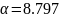 )
является положительной, то колебания
будут расходящимися
)
является положительной, то колебания
будут расходящимися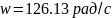 ,
периодом
,
периодом
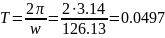 ,
коэффициентом расхождения
,
коэффициентом расхождения
и декрементом расхождения:
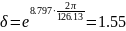
4.Расчет и построение частотных характеристик эквивалентной разомкнутой сау: афчх, лачх, лфчх. Определение устойчивости по частотным характеристикам.
y
z



g




![]()
![]()
21.234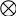

Рис.4. Структурная схема разомкнутой САУ
Разомкнутая САУ– система, не способная контролировать состояние объекта управления, т.е. это САУ без обратной связи. Передаточная функция разомкнутой САУ выглядит следующим образом:
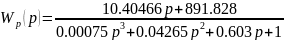
Комплексно-частотная функция имеет вид:

Введём подстановку:
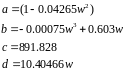
и преобразуем полученное выражение:

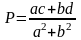 ;
;
 ;
;
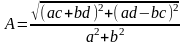 ;
;

Подставим числовые значения


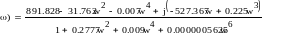 -АФЧХ.
-АФЧХ.

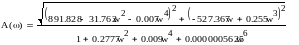 -АЧХ.
-АЧХ.
 - ЛФЧХ.
- ЛФЧХ.
Логарифмические частотные характеристики определяют усилительные свойства системы (ЛАЧХ) и сдвиг фазы выходной величины (ЛФЧХ) в логарифмическом масштабе.
ЛАЧХ – модуль комплексной функции АФЧХ с учетом логарифмического масштаба, а ЛФЧХ – аргумент комплексной функции.
Уравнение ЛАЧХ:

Р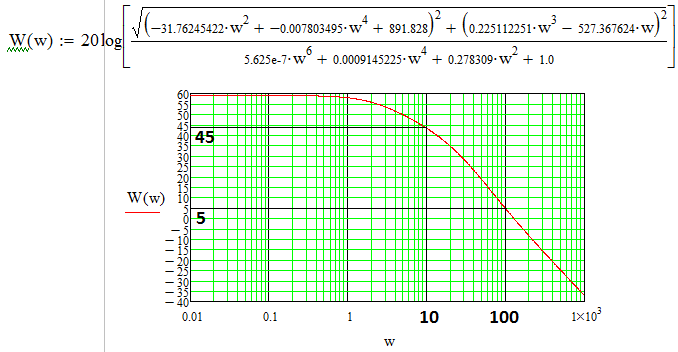
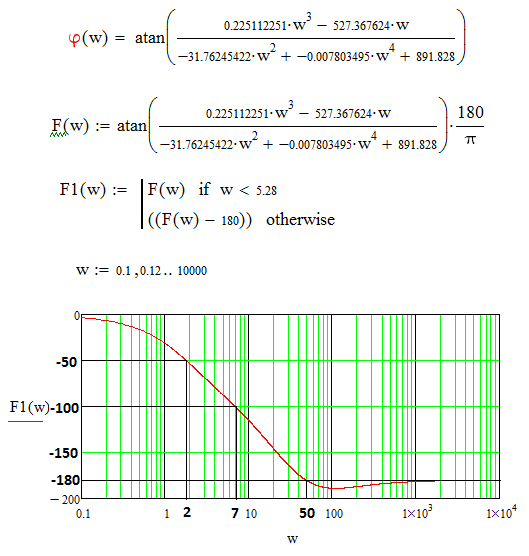 исунок
5. ЛАЧХ, построенная в Mathcad
исунок
5. ЛАЧХ, построенная в Mathcad

Рисунок 6. ЛФЧХ, построенная в Mathcad
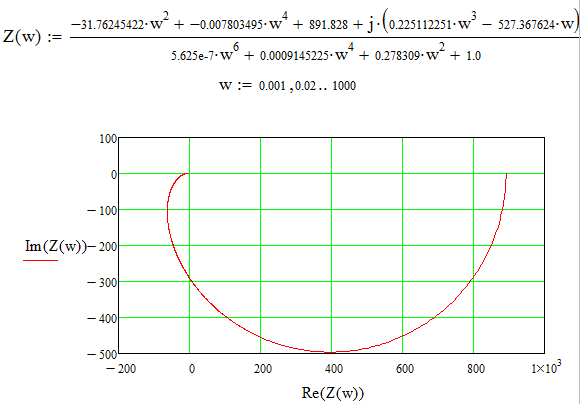
Рисунок 7. АФЧХ, построенная в Mathcad
 Построим
с помощью пакета MatLab
логарифмическую амплитудную частотную
характеристику (ЛАЧХ), фазово-частотную
характеристику (ЛФЧХ) и амплитудную
фазово-частотную характеристику (АФЧХ)
для разомкнутой системы. Структурная
схема разомкнутой САУ в среде MatLab
Построим
с помощью пакета MatLab
логарифмическую амплитудную частотную
характеристику (ЛАЧХ), фазово-частотную
характеристику (ЛФЧХ) и амплитудную
фазово-частотную характеристику (АФЧХ)
для разомкнутой системы. Структурная
схема разомкнутой САУ в среде MatLab

Рисунок 8. Схема разомкнутой САУ в MatLab
.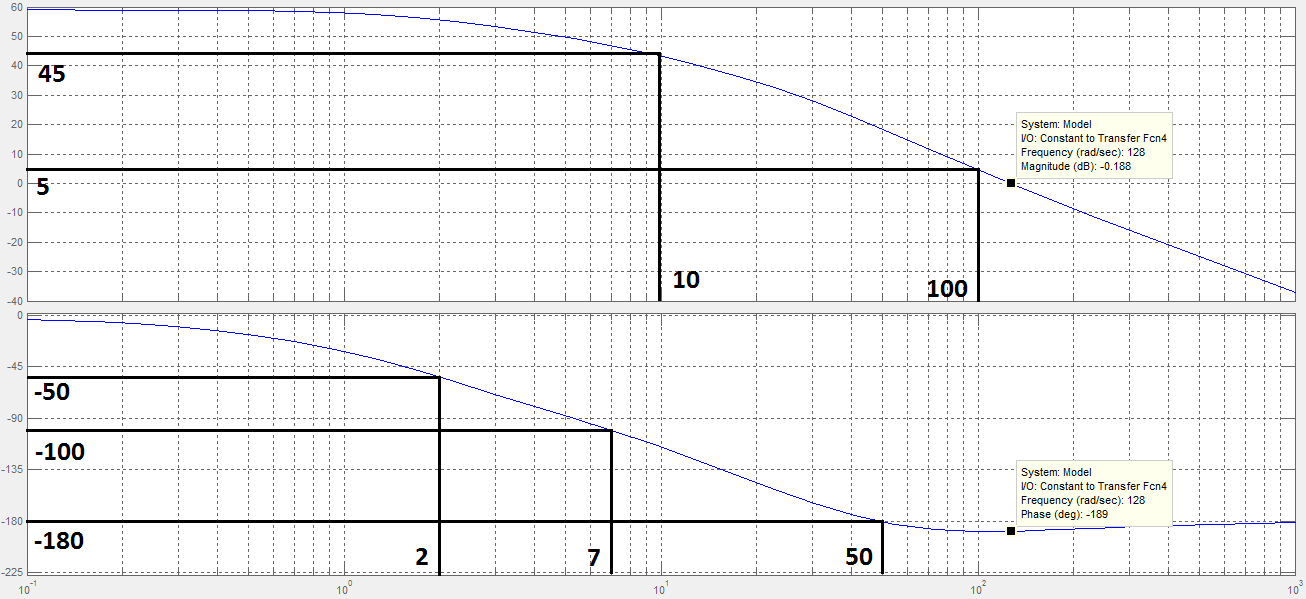
Рис.9 Графики ЛАЧХ (сверху) и ЛФЧХ (снизу) разомкнутой САУ
Запас по фазе на частоте единичного усиления отсутствует
Запас
по амплитуде:

Передаточная функция разомкнутой САУ имеет вид:
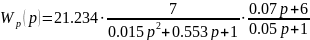

 Определим
коэффициент демпфирования:
Определим
коэффициент демпфирования:

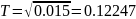
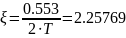
Т.к. ξ≥1 то можно данное звено заменить на 2 апериодических звена первого порядка.
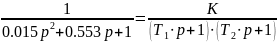
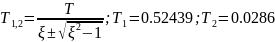

Запишем все звенья после некоторого преобразования.
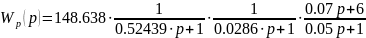


Найдём частоты сопряжения:

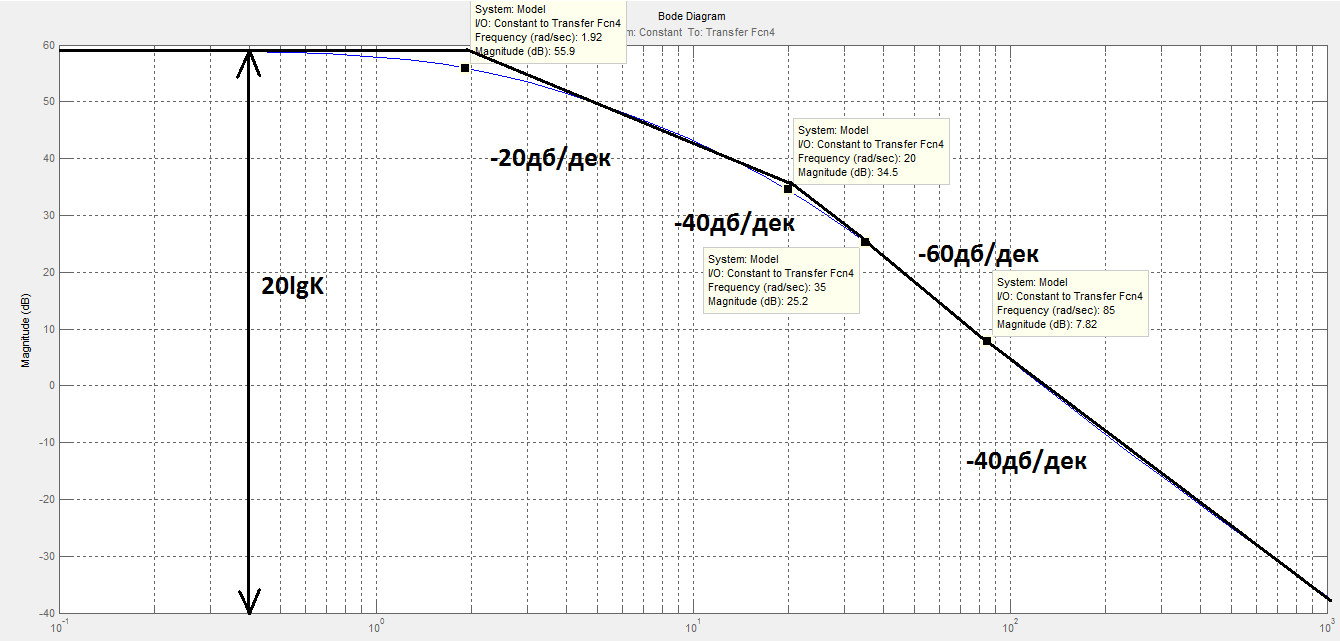
 Рис.10
График ЛАЧХ разомкнутой САУ
Рис.10
График ЛАЧХ разомкнутой САУ
Так как частоты сопряжения находятся вблизи друг друга проводим моделирование отдельных частей системы для уточнения характера процесса:
Убираем
звено, срабатывающее на частоте
 рад/с
рад/с

Р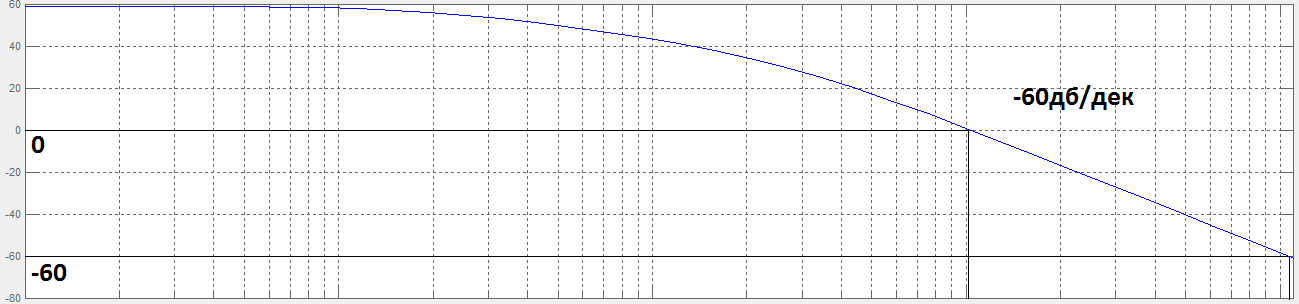 исунок
11 Модель в MatLab
исунок
11 Модель в MatLab
Рисунок 12. ЛАЧХ
Убираем
звено, срабатывающее на частоте
 рад/с
рад/с

Р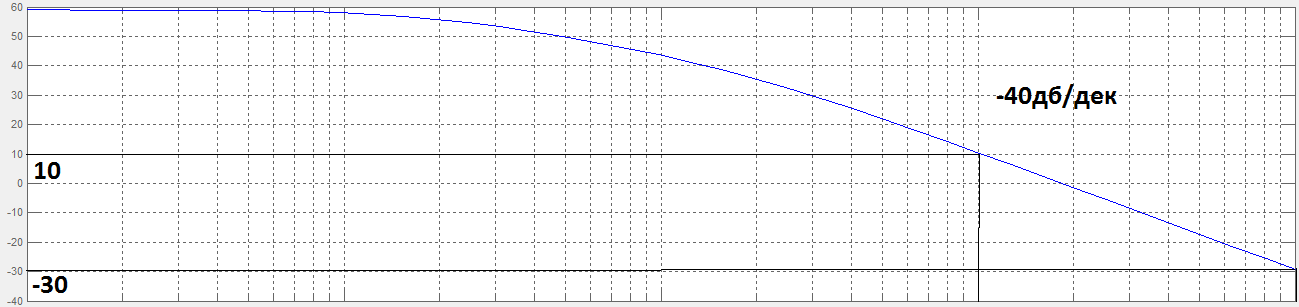 исунок
13 Модель в MatLab
исунок
13 Модель в MatLab

Рисунок 14. ЛАЧХ
Убираем
звено, срабатывающее на частоте
 рад/с
рад/с
Р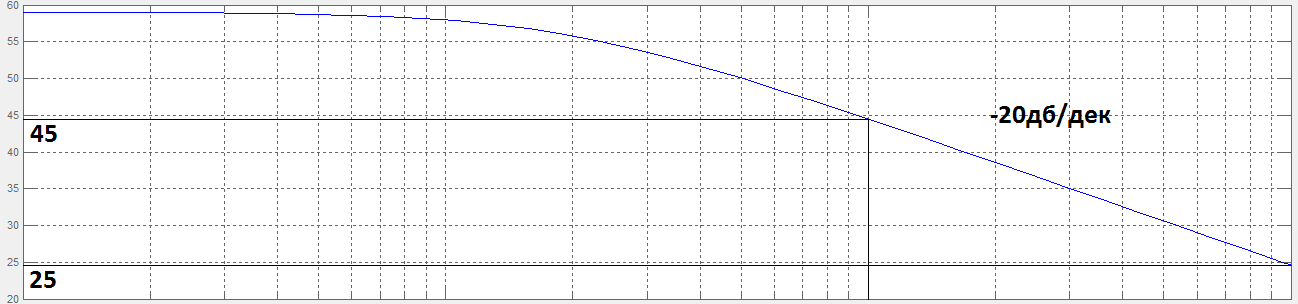 исунок
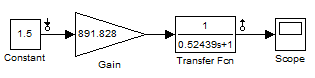
15 Модель в MatLab
исунок
15 Модель в MatLab
Рисунок 16. ЛАЧХ


Рис.17. График АФЧХ разомкнутой САУ
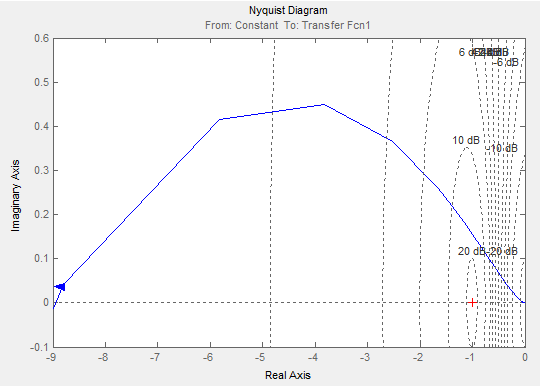

Рис.18. Увеличенный участок АФЧХ разомкнутой САУ
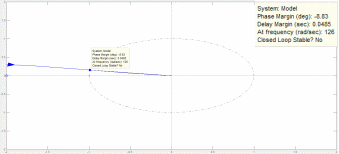
Рис.19. Увеличенный участок АФЧХ разомкнутой САУ
Критерий устойчивости по Найквисту предназначен для определения устойчивости замкнутых систем по частотным характеристикам эквивалентных разомкнутых цепей.
Формулировка
критерия: «Если разомкнутая система
устойчива, то для устойчивости
соответствующей замкнутой системы,
необходимо, чтобы АФЧХ разомкнутой цепи
не охватывало точку
 на
комплексной плоскости».
на
комплексной плоскости».
Вывод: система неустойчива.
