4. Визначення виразів для струмів та напруг

Вирази для решти струмів та напруг визначаються з системи рівнянь, які складені за законами Кірхгофа (5.40):

. (5.50)

Вираз для струму і₂ отримується з другого рівняння системи (5.40) після підстановки виразів (5.50) та (5.37):

. (5.51)

Вираз для напруги U_c конденсатора отримується з третього рівняння системи (5.40):

. (5.52)

Струм конденсатора і_С визначається з виразу після підстановки до нього рівняння (5.52):

. (5.53)

6. Методичні вказівки з розрахунку перехідних процесів у ланцюгах при дії джерела, яке змінюється за синусоїдальному закону

Рівняння, що визначає будь-яку змінну кола (струми в вітках, напруги на елементах), у загальному випадку містить дві складові: примусову і вільну. Вільна складова визначається розв’язком однорідного диференціального рівняння, тобто рівнянням без правої частини. Тобто вигляд вільної складової не залежить від виду джерела, що діє в колі, а визначається тільки схемою з'єднання елементів кола та їхніх параметрів.

Примусова складова шуканої змінної залежать від виду джерела, що діє в колі. Розрахунок примусової складової при дії джерела синусоїдальної форми виконується в комплексній формі.

Крім розрахунку примусової складової, необхідно приділити увагу на визначення початкових умов при розрахунках постійних інтегрування. У цьому випадку проводиться розрахунок значень струмів і напруг у комплексній формі для кола до комутації. Потім знайдені значення змінних записуються в синусоїдальній формі, і в отримані вирази підставляється t = 0. Розглянемо розрахунок початкових значень змінних на прикладі кола, наведеного на рис.6.1.

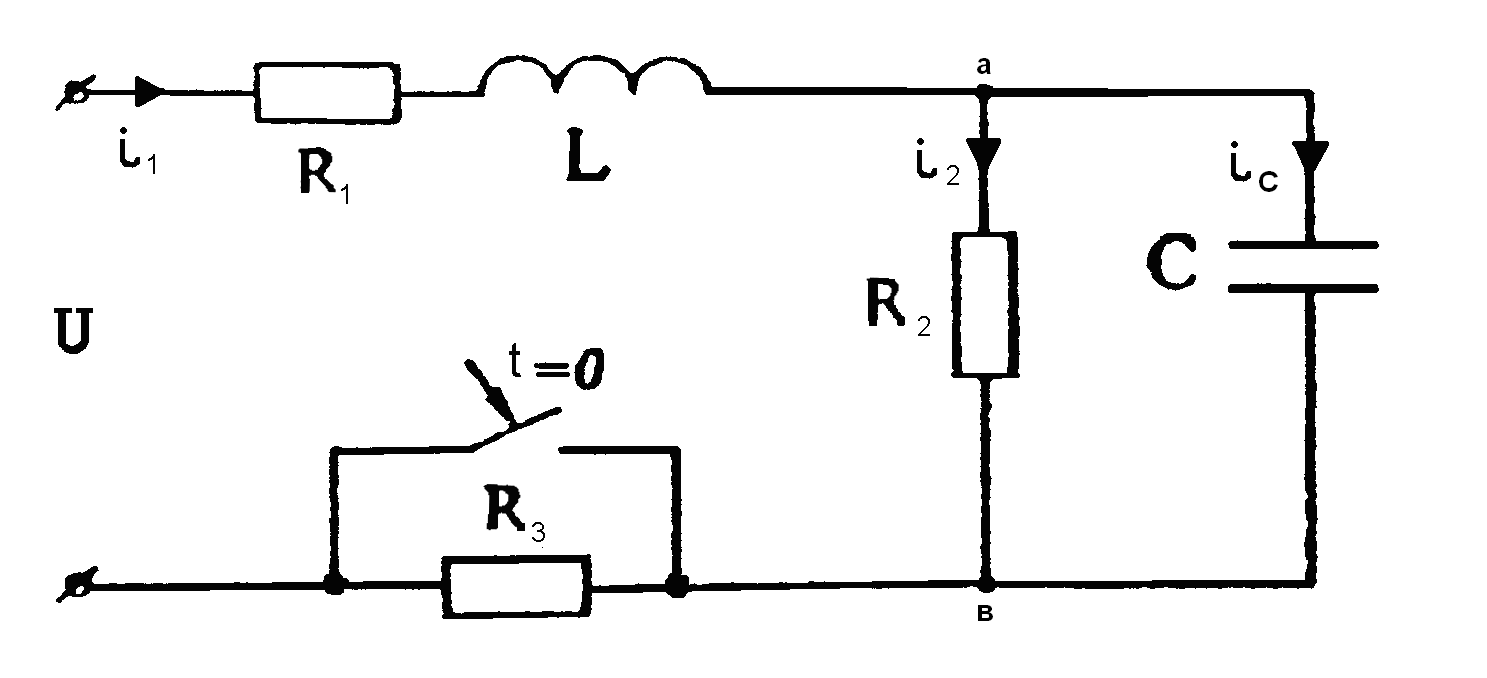
Рис. 6.1

На вході кола діє напруга, що змінюється за синусоїдальним законом:

Визначимо струми в вітках схеми комплексним методом.

Запишемо напругу джерела в комплексній формі:

.

Визначаємо струм кола до комутації:

,

де . (6.1)

Тоді вираз для струму в комплексній формі буде мати вигляд:

.

Виразимо струми і через параметри кола:

(6.2) (6.3)

Тоді вираз для струмів і будуть мати наступний вид:

(6.4)

Запишемо струми кола в синусоїдальній формі:

(6.5)

Підставимо в отримані вирази t = 0 та знайдемо значення цих струмів в момент часу безпосередньо перед комутацією:

(6.6)

Аналогічно знаходять початкові значення напруг на елементах кола.

7 Методичні вказівки з розрахунку перехідних процесів операторним методом

7.1 Загальна методика розрахунку перехідних процесів операторним методом

7.1.1 Основні положення та співвідношення

В основу операторного методу покладене наступне:

функція , що є струмом і(t), або напругою u(t), яка називається оригіналом , замінюється відповідною їй функцією F(p) комплексної змінної р , яка називається зображенням.

Ці функції зв'язані співвідношенням, що є прямим перетворенням Лапласа:

(7.1)

або

. (7.2)

При такому перетворенні операція диференціювання над функцією дійсної змінної f (t) замінюється операцією множення на оператор р функції комплексної змінної F(p). B свою чергу, операція інтегрування замінюється операцією ділення на оператор р.

У таблиці 7.1 приводяться оригінали найпростіших функцій та їхнього зображення, отримані за формулою (7.1).

Таблиця 7.1

Оригінал	Зображення	Оригінал	Зображення
1. 1		8.
2. t		9.
3.		10.
4.		11.
5.		12.
6.		13.
7.		14.

Схеми заміщення реактивних елементів, складені за формулою (7.1), кола з нульовими початковими умовами наведені на рис. 7.1.

Індуктивний елемент Ємнісний елемент

_JL

Cp

Рис. 7.1