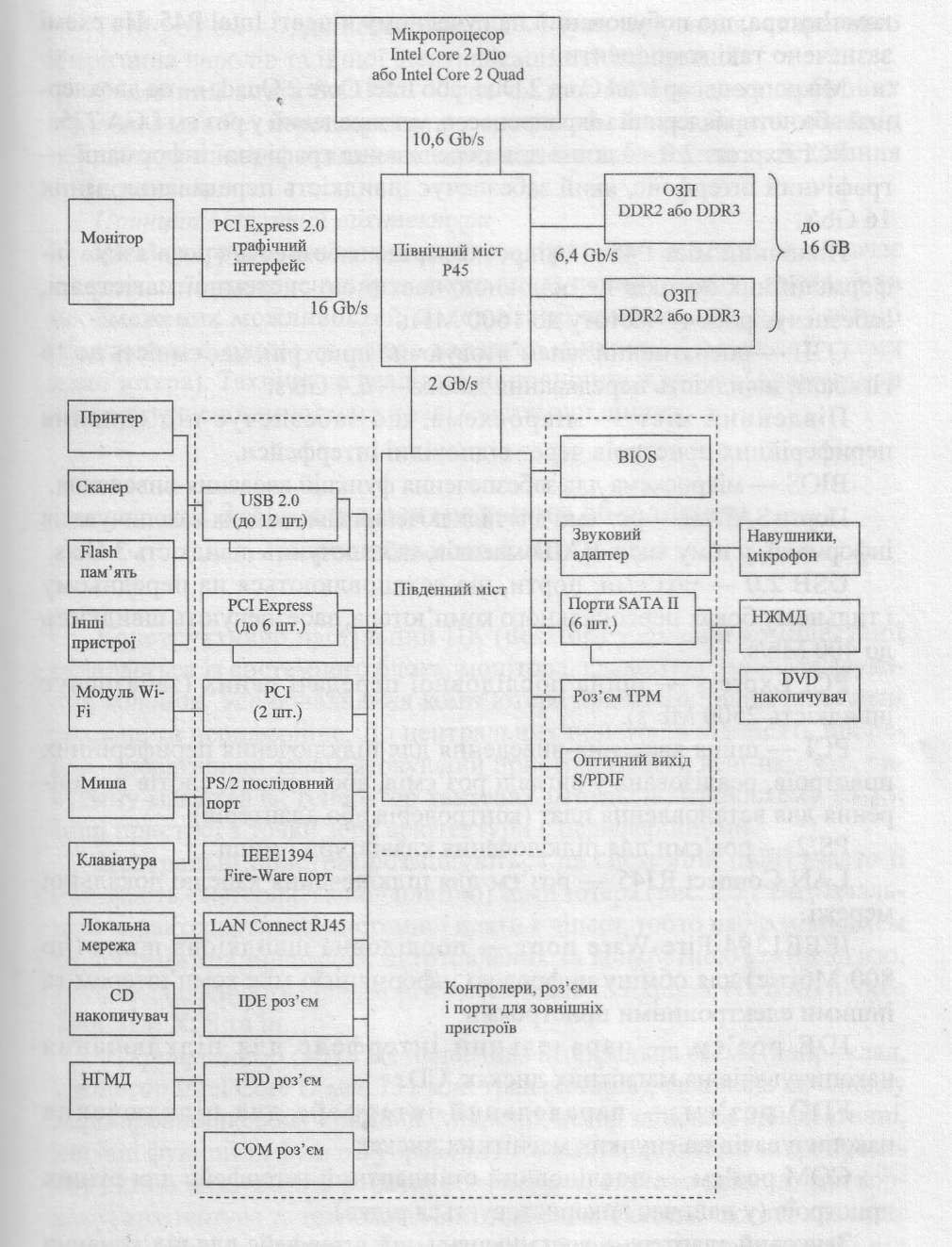
Приклад архітектури пк

Аудиторне заняття №3 Системи числення

Системою числення називають систему відоб­раження будь-яких чисел за допомогою обмеженого числа знаків.

Залежно від способів відображення чисел цифрами, системи числення діляться на позиційні і непозиційні.

Непозиційною системою числення нази­вають систему, в якій кількісне значення кожної цифри не залежить від місця у відображенні числа, а визначається лише самим симво­лом числа. Так, наприклад, число ЗО десяткової системи числення в римській непозиційній системі позначають як число XXX, яке має у всіх розрядах один і той же самий символ X, що означає 10 оди­ниць незалежно від його позиції у відображенні числа.

Позиційною системою числення називають систему, в якій кількісне значення кожної цифри залежить від її мі­сця у відображенні числа. Наприклад, число 575, представлене в десятковій системі числення, має в найстаршому і наймолодшому розрядах цифру 5. Цифра 5 у старшому розряді має вагу в 100 раз більшу, ніж у молодшому розряді.

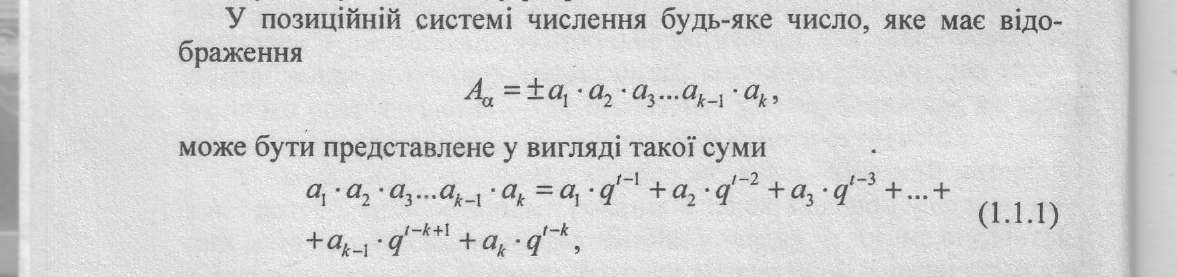
де k — кінцева кількість розрядів у відображенні числа; a_i — цифра і-го розряду; g — основа системи числення; t — фіксоване число, яке визначає положення коми; і — порядковий номер розряду; g ^t-i — вага i-го розряду.

Цифри a_i повинні задовольняти нерівності

Основою системи числення g називають кі­лькість символів, які використовують для відображення числа в да­ній позиційній системі числення.

За основу системи числення д мають будь-яке число, яке задо­вольняє умові У двійковій системі числення д g = 2 і для зображення чисел ви­користовують символи (1, 0), у вісімковій g = 8 і для зображення чисел — символи (0, 1, 2, 3, 4, 5, 6, 7), а у шістнадцятковій — g = 16 і для зображення чисел символи — (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, Д Е, Е), де А = 10; B= 11; С = 12; D= 13; Е = 14; F = 15.

Двійкова система числення є основною системою числення, в якій виконують арифметичні і логічні операції в комп'ютерах, тому що для її технічної реалізації широке застосування знайшли двох- позиційні електронні елементи.

Суттєве значення при виконанні арифметичних та логічних опе­рацій у комп'ютерах має переведення чисел із десяткової системи числення в двійкову, вісімкову та шістнадцяткову і навпаки. Для переведення цілих чисел найчастіше використовують алгоритм ді­лення заданого числа на основу числа, в систему якої його перево­дять. Даний алгоритм переведення чисел із системи числення з ос­новою д є універсальним і найбільш широко застосовується на практиці. Він має такі кроки.

1. Розділити число, яке переводять, у системі числення з осно­вою g на основу р за правилом системи числення з основою g.

2. Перевірити, чи не дорівнює частка нулю. Якщо не дорівнює, то прийняти її за нове число й повернутися до кроку 1.

3. Якщо частка дорівнює нулю, то виписати всі отримані зали­шки від ділення в порядку, зворотному їх отриманню.

4. Отриманий запис є записом числа в системі числення з осно­вою р.

Нижче в таблиці 1 наведені перших 16 натуральних чисел записаних в десятковій, двійковій, вісімковій та шістнадцятковій системах числення.

Таблиця 1

Приклад Перевести число 13₍₁₀₎ десяткової системи чис­лення у двійкову й виконати перевірку розв'язку.

Розв'язання. У відповідності з алгоритмом переведення цілих чисел ділимо послідовно число 13 десяткової системи числення на основу двійкової системи числення (число 2), в результаті чого отримаємо

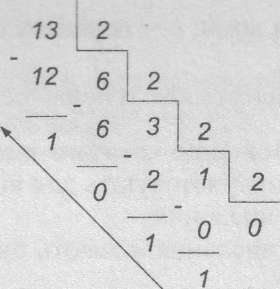
13 ₍₁₀₎ =П01₍₂₎.

Для перевірки записуємо формулу пере­ведення чисел двійкової системи числення у десяткову

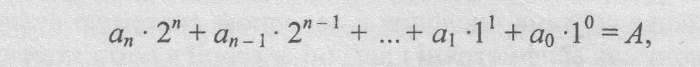
де a_n, a_n-1,….., a₁, a₀ - цифри двійкового числа, які приймають зна­чення 0 або 1;

А — ціле десяткове число.

Використовуючи формулу, отримаємо 1*2³+1*2²+0*2¹+1*2⁰=13₍₁₀₎