1.3. Упрощённая запись оператора Лизеганга

Для дальнейшего рассмотрения проблемы необходимо решить вопрос о постановке математической задачи в неограниченной области. В этом случае необходимо указать поведение концентрации нанокластеров на бесконечности. Чтобы ответить на этот вопрос, следует прояснить вопрос о взаимодействии коллоидных кластеров и межмицеллярной жидкости. Естественно полагать, что в некоторой пространственной области гелевые кластеры не взаимодействуют с гелевой средой. Это совершенно объяснимо, так как крупные макромолекулярные гелевые образования практически не перемещаются в объеме. Диффузия их замедленна, центры масс практически неподвижны.

Напротив, в ограниченной области пространства коллоидные кластеры интенсивно взаимодействуют со средой и друг с другом. Это взаимодействие осуществляется через конформерное движение гелевых макрообразований или процессов (полимеризационно- пептизационных), близких к ним, вследствие динамического явления схлопывания или “разрыва” ДЭС макромолекул с выбросом в дисперсионную среду, например, подвижных нанокластеров и созданием новых стабилизированных ДЭС иного объема.

Возникает вопрос о том, как мы можем разграничить две эти области. Можно предположить, что в области «невзаимодействия» частичная концентрация коллоида невелика, и его пространственные изменения недостаточны, чтобы их можно было обнаружить экспериментально. Проще всего задать такое взаимодействие дифференциальным уравнением, решение которого есть убывающая показательная функция. В области же взаимодействия, наоборот, концентрация коллоидных нанокластеров заметно изменяется и это может быть зафиксировано, вообще говоря, экспериментально.

Для решения этой проблемы разобьём область на две части: неограниченную, «область невзаимодействия», и ограниченную, «область взаимодействия», и попробуем оценить их размеры и амплитуду концентраций на границе областей и в центре области взаимодействия. Для этого будем считать, что в «области взаимодействия» скорость изменения коллоидных кластеров растёт пропорционально массе имеющегося коллоида, а в «области невзаимодействия» - уменьшается с такой же скоростью. В этом случае задача имеет вид:

(1.3.1)

(1.3.2)

здесь 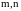- концентрации в областях «взаимодействия» и «невзаимодействия». На границе между ними поставлено условие согласования концентрации и её производной. Примем, что в начальный момент времени концентрация кластеров, отличная от нуля, возникла только в области «взаимодействия», и она равна .

Построим решение задачи (1.3.1). Проводя преобразование Лапласа по времени в этой задаче (1.3.2), получим уравнение

(1.3.3)

где использовано выражение , 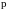- параметр преобразования Лапласа. Решение головного уравнения системы имеет вид: 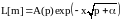, где величина 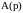должна быть определена из условий согласования концентрации и её производной на границе областей «взаимодействия» и «невзаимодействия».

Аналогично, проводя преобразование Лапласа в уравнении (5.3.1), получаем решение в виде: , где , , и определитель Вронского . Таким образом, решение зависит от величины и начального условия .

Выражение можно разложить в ряд. Считая, что , получим: . Эти выражения будут умножаться на показательные функции сходного вида: и . Кроме того, в знаменателе будет выражение . Каждое из этих выражений в отдельности имеет обратное преобразование Лапласа. Выражение вида 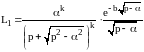имеет вид свёртки: . Таким образом, мы можем обратить всю правую часть, получив решение в явном виде - в виде рядов.

Точно построить обращение преобразования Лапласа в этом случае затруднительно, но можно строить приближения с достаточно большой точностью. Для этого можно разложить знаменатель в ряд и вычислить несколько его первых членов. Решение для разного числа членов приводится ниже на рис.1.4.

Можно для иллюстрации рассмотреть решение в частном случае. Для этого выберем 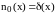. Тогда решение примет вид: . Удобно рассмотреть его при 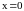, т.е. 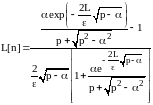. Разлагая выражение в ряды, получим: . Обращая преобразование Лапласа, имеем:

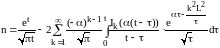. Несколько графиков приведено на рисунке.

Рис.1.4