1

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Челябинский государственный университет»

Ю. И. Сухарев

Оптические свойства гелевых оксигидратов

и их каустики

Текст лекций

Челябинск

Издательство Челябинского государственного университета

2013

Печатается по решению редакционно-издательского совета Челябинского государственного университета

Рецензенты: кафедра водного хозяйства и технологии воды Уральского федерального университета; А.Ф. Никифоров, доктор химических наук, профессор; кафедра физической и коллоидной химии Уральского федерального университета; В.Ф. Марков, доктор химических наук, профессор

Сухарев, Ю.И.

Оптические свойства гелевах оксигидратов и их каустики : курс лекций / Ю.И. Сухарев. Челябинск : Изд-во Челяб. гос. ун-та, 2013. 198 с.

ISBN 000-0-0000-0000-0

В основу лекций положены представления о колебательных процессах, которые широко распространены в природе. Рассмотрен вид оператора Лизеганга и соответствующая ему фазовая диаграмма, прошедшего через гель оптического электромагнитного поля. Показан спиралеобразный вид распределения кластеров в гелевом пространстве следствием чего является периодическое изменение интенсивности падающего на гелевую пластину электромагнитного излучения к интенсивности прошедшего. Установлено влияние пульсационного шума или тока самоорганизации в магнитном поле на особенности оптических характеристик оксигидрата иттрия, а также на кинетические кривые изменения оптической плотности оксигидратных систем.

Предназначено для аспирантов, обучающихся по специальности 020021 «химия твердого тела».

Табл. 10. Ил. 71. Библиогр.: 86 назв.

ISBN 000-0-0000-0000-0

© ФГБОУ ВПО «Челябинский государственный университет», 2013

Оглавление

Вводная лекция КЛАСТЕРНО-ЭЛЕКТРИЧЕСКАЯ АУРА КОЛЛОИДНО-ХИМИЧЕСКИХ ОКСИГИДРАТНЫХ СИСТЕМ………………………………5

Лекция 1. Оператор Лизеганга 7

1.1. Оператор Лизеганга как отражение колебательных свойств гелевых полимерных систем. Введение оператора Лизеганга 7

1.2. Исследование сильно нелинейного уравнения диффузии 12

1.3. Упрощенная запись оператора Лизеганга 25

1.4. Гидродинамический подход 35

1.5. Оператор Лизеганга и некоторые экспериментальные данные 37

Список рекомендуемой литературы 46

Лекция 2. Оптические свойства гелевых оксигидратов и размеры

кластеров 48

2.1. Уравнение поглощения света на конформерных «шумовых

кластерах» 48

2.2. Связь с оператором Лизеганга 54

2.3. Влияние пульсационного шума или тока самоорганизации в магнитном поле на особенности оптических характеристик оксигидрата иттрия 57

2.4. Кинетические кривые оптической плотности некоторых гелей оксигидратных систем 63

2.5. Интерферационный подход к экспериментальному определению средних размеров ионных кластеров оксигидратных гелей d- и f-элементов 73

2.6. Вычисление размеров кластеров на примере гелей оксигидратов кремния и иттрия 81

Список рекомендуемой литературы 89

Лекция 3. Каустики стохастических потоковых кластеров и решение задачи формообразования самих кластерных частиц 93

Список рекомендуемой литературы 108

Лекция 4. Каустики лагранжевых отображений гелевой оксигидратной магнитной жидкости железа 109

4.1. Введение 109

4.2. Типичные перестройки каустик в трехмерном пространстве лагранжева многообразия 115

4.3. Анализ экспериментальных результатов 128

Список рекомендуемой литературы 136

Лекция 5. Форма и механизм разряда волновых стохастических кластеров вблизи регистрирующих электродов 137

Список рекомендуемой литературы 137

Лекция 6. Новые принципы исследования несовершенных кристаллографических форм коллоиднохимических кластеров 170

Список рекомендуемой литературы 196

Вводная лекция

Колебательные процессы широко распространены в природе. Характер колебательного процесса может быть как пространственный, так и временной. Так, в геологии колебательный характер можно проследить у агатов, яшм, малахитов, крокидолитов, сталактитов, в различных рудных жилах, параллельно-ленточных структурах в почвах, песке, глинах, во внутренней зонарности кристаллов, в лучистых структурах. Отчасти эти структуры определяются периодичностью явлений в природе вообще (смена времён года, и др.).

Периодичность в процессах жизни и продуктах жизнедеятельности: периодическое и лучистое строение колоний организмов, периодическое и лучистое строение отдельных организмов, отдельных тканей, камней, образующихся в органах, периодические процессы, например, возбуждение в нервных волокнах, мышечные сокращения и т.д.

Вслед за книгой Ф.М. Шемякина и П.Ф. Михалёва [1], можно классифицировать рассмотренные процессы по группам: химические, физико-химические и физические процессы.

Нас интересует прежде всего периодическая кристаллизация, периодическая диффузия, периодическая адсорбция, периодическая конденсация, периодическая коагуляция, периодическое высаливание, хемотаксис, периодические явления поверхностно-активных веществ, искусственные наслоения Лизеганга, наслоения сажи, периодичность при застывании металлов, фигуры деформации при пробое металлов, периодические процессы при седиментации металлов.

Таким образом, можно сделать вывод, что и периодические процессы в коллоидной химии чрезвычайно распространены, учитывая их практически всеохватное нахождение. Важнейщая роль их исследования отводится когерентной химии, химии колебательно-периодических процессов. Но тут есть определённая сложность: в классической неорганической химии и коллоидной химии колебательная парадигма развития явлений и процессов очень слабо развита и практически не разработана и не понята. Следовательно, мы упускаем из поля зрения многие тонкие коллоидно-химические явления, которые могут быть весьма существенными и значимыми, например, при адсорбции и катализе.

Оксигидратные гелевые системы (ГОС) редкоземельных элементов, а также оксиды-гидроксиды некоторых d – элементов, таких как цирконий, ниобий, титан и другие, интересны тем, что, являясь весьма труднорастворимыми, склонны к диссоциации по кислотно-основному механизму, а, следовательно, к проявлению ионообменных и адсорбционных свойств. Их свойства слабо или совсем не воспроизводимы, хотя, казалось бы, предприняты все усилия и средства для полного воспроизведения начальных параметров. Долгое время усилия исследователей были направлены на решение именно этой задачи.

Разрабатывались разнообразные методы синтеза, как ожидалось, могущие привести к желаемому результату. Распространенными методами получения сорбентов являются: катионное легирование оксигидратов (получение смешанных сорбентов), термическая обработка (гидротермальный синтез), направленная термическая кристаллизация, а также ионный аппликационный синтез. Исследователи ожидали, что только сильным воздействием (высокими температурой, давлением, высококонцентрированной средой (раствором)) удастся создать воспроизводимый синтез гелевых систем, то есть удастся получить гели с высокими сорбционно-селективными параметрами, высокой избирательностью.

Однако этим надеждам практически не суждено было сбыться. Причина этих неудач кроется в нелинейных особенностях различных характеристик гелевых оксигидратов [2].

Гелевые оксигидратные системы в определенной мере обладают фрактальными, а, следовательно, мезофазоподобными свойствами. Это обстоятельство само по себе весьма многозначно, так как заставляет учитывать самоорганизующий характер взаимодействия частиц в гелевой системе.

Полимерно - конформационное разнообразие энергетически близких гелевых фрагментов, которые непрерывно трансформируются под действием, например, тепла диссипации системы, является исходным положением нашего исследования о пульсационно-колебательном характере существования (движения) гелевых организаций даже в воздушно сухом состоянии.

Исследования нелинейных свойств гелевых оксигидратных систем обнаружили следующие явления [3,4]: колебательную дилатантность, колебательную (пульсационную) электрическую проводимость, самопроизвольный электроток гелевой самоорганизации на фоне поляризационных явлений, окрашенность гелевых систем, колебательные сорбционные и оптические свойства, которые мы предлагаем рассмотреть в данной книге более подробно. Исследуются также совершенно новые оптические характеристики пульсационных оксигидратных систем – коллоидно-химические каустики, ответственные за формирование структуры [5].

Лекция 1. Оператор Лизеганга

1. Оператор Лизеганга как отражение колебательных свойств гелевых полимерных систем. Введение оператора Лизеганга.

В [6,7] нами введен оператор Лизеганга для описания и анализа волновых свойств гелевых систем, дана его теория, насколько она была нами понята в то время. В разделах 1.7 и 2.4 монографии [4] применение оператора Лизеганга к расчету экспериментальных результатов позволило рассчитать кластерные размеры структурных элементов гелевой оксигидратной системы циркония, которые не противоречат (совпадают) экспериментальным значениям, установлен механизм хаотизации гелевой системы ГДЦ, то есть установлено удвоение периода колебательных циклов по Фейгенбауму.

Представляется необходимым рассмотреть сильно нелинейные уравнения, которые необходимо вводить для описания кластерного состояния гелей. Пусть осадок контактирует с маточной дисперсионной средой структурированной фазы, часть матрицеформирующего элемента (циркония) переходит в осадок (адсорбируется структурированной фазой), затем может пептизировать и переходить вновь в раствор. Считаем, что гель в дисперсионной фазе трансформируется в структурированное состояние в соответствии с периодическим законом (в предыдущих разделах это экспериментально и теоретически показано), и связь между массой растворяемого геля и адсорбированной массой может быть задана периодической диаграммой. Одна из таких простейших диаграмм приведена на рис. 1.1.

Рассмотрим эту диаграмму подробнее в целях иллюстрации.

Простейшая диаграмма 1.

Рис.1.1.

Фазовая диаграмма геля в растворе.

- масса растворённого геля, - производная массы геля по времени, - время. Заметим, что радиус окружности и форма диаграммы может зависеть от значения .

Удобно параметризовать диаграмму следующим образом:

(1.1.1)

где величина - некая постоянная.

Решение для : , то есть существует периодическое решение для изменения массы над остатком. Отметим, что это уравнение имеет и побочные решения.

Удобно перейти от массы геля к молярной или иной частичной концентрации. При этом учтём, что полная производная массы по времени будет зависеть и от пространственных координат системы. В результате получим систему для функции-параметра :

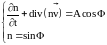(1.1.2)

где - гидродинамическая скорость. Если же необходимо рассмотреть уравнение диффузии, то заметим, что в этом случа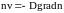е , где - коэффициент диффузии. Тогда система перепишется в виде:

(1.1.3)

где - оператор Лапласа. Заметим, что в этих уравнениях для коллоидов d- и f- элементов учтена синхронизация изменения концентрации во всех пространственных точках.

Систему (1.1.3) для разных фазовых диаграмм удобно переписывать и в другой форме. Если обозначить через , то получаем соотношение . Подставим его в правую часть выражения (1.1.3), то получаем . Выражение 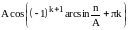назовём оператором Лизеганга и будем обозначать как .

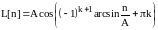Определение. Оператором Лизеганга назовём такую форму записи сильно нелинейного уравнения (1.1.3), которая сводит сильно нелинейное уравнение к обычному нелинейному уравнению со сложной формой записи правой части. Фактически это уравнение фазовой паутины Заславского [8].

Отметим, что тот же физический смысл имеет и другая форма записи оператора Лизеганга: , где - некоторые числа. В этом случае уравнение с оператором Лизеганга принимает вид: .

Заметим, что выражение можно переписать в виде: . Фазовая диаграмма в этом случае принимает вид:

Рис. 1.2

Графики фазовой зависимости при разных ,

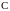где , . Отметим, что важный случай на графике представлен границами квадратов. Это – единственная фазовая линия, соединяющая несколько диаграмм.

Отметим, что система (1.1.3) – частный случай выражения . Для обобщения результатов удобно записать максимально общую форму уравнений, даже если её физический смысл неочевиден.

Общая форма записи оператора Лизеганга. Самая общая форма записи сильно нелинейного дифференциального уравнения с точки зрения математической формы имеет вид:

, .

Заметим, что в этом случае запись оператора Лизеганга в явной форме затруднительна, а в неявной – задаётся этой парой парметрических соотношений.

Определение. Назовём общим уравнением Лизеганга сильно нелинейное уравние

или общим оператором Лизеганга является выражение через , где ,

. (1.1.4)