2.5 Описание разработанной программной системы
Программная система была реализована в интегрированном пакете C++ Builder 5.0. Внешний вид окна программы представлен на рисунке 5.
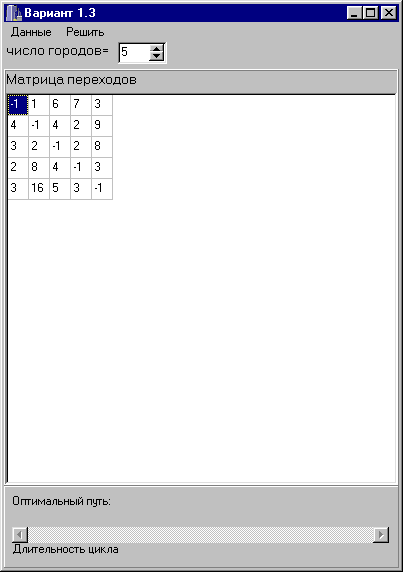
Рис. 5 - Внешний вид программы
В верхней части окна пользователю необходимо ввести количество городов, которое необходимо посетить коммивояжёру, а также матрицу расстояний. После того как пользователь ввёл все необходимые параметры задачи, ему необходимо выбрать из меню «Решить» каким методом решать задачу. Все полученные значения будут выведены в нижней части окна программы.
Если при вводе параметров будет допущено нарушение формата, программа даст соответствующее сообщение и предложит пользователю заменить неподходящее значение на допустимое.
3 Численные эксперименты
3.1 Ручная реализация алгоритма решения задачи с помощью алгоритма Литла
На данном этапе необходимо выполнить ручной просчёт на основании данных, взятых из задания к курсовой работе.
Шаг 1. Приводим матрицу:
->
->
->
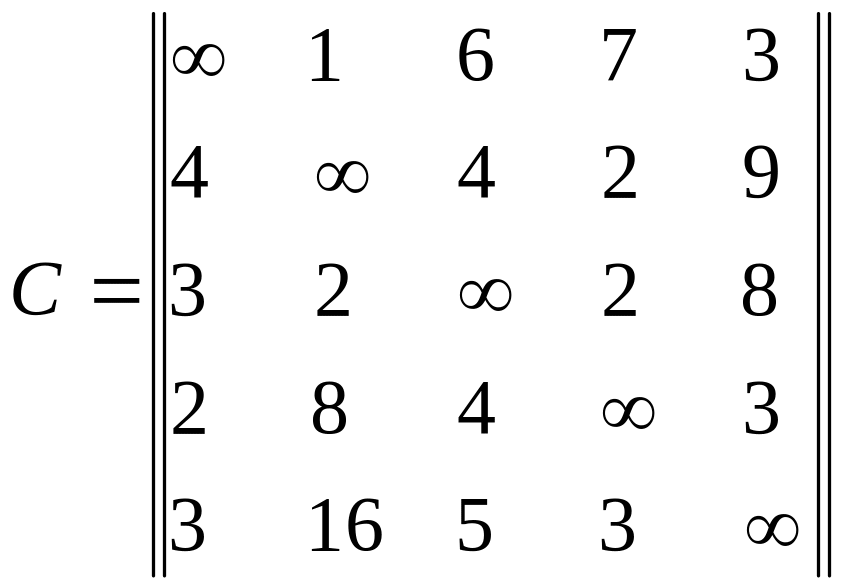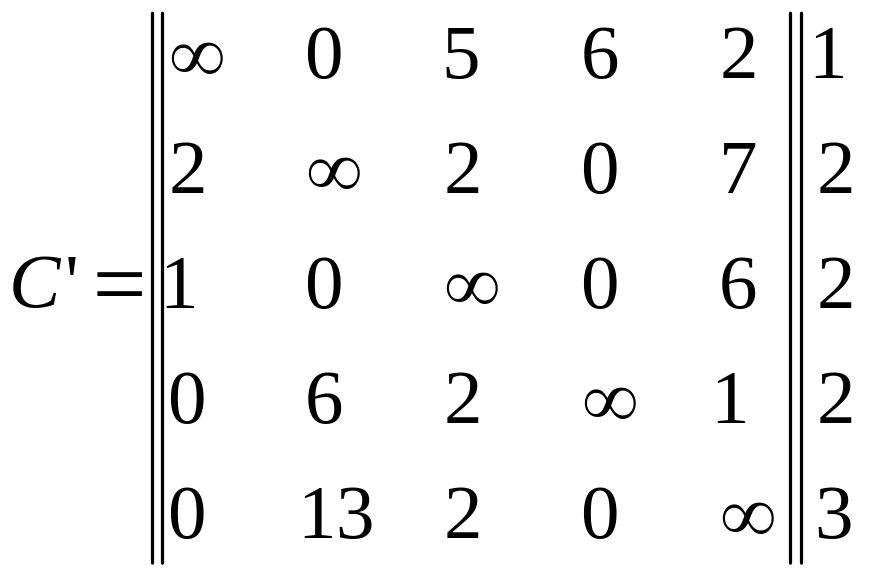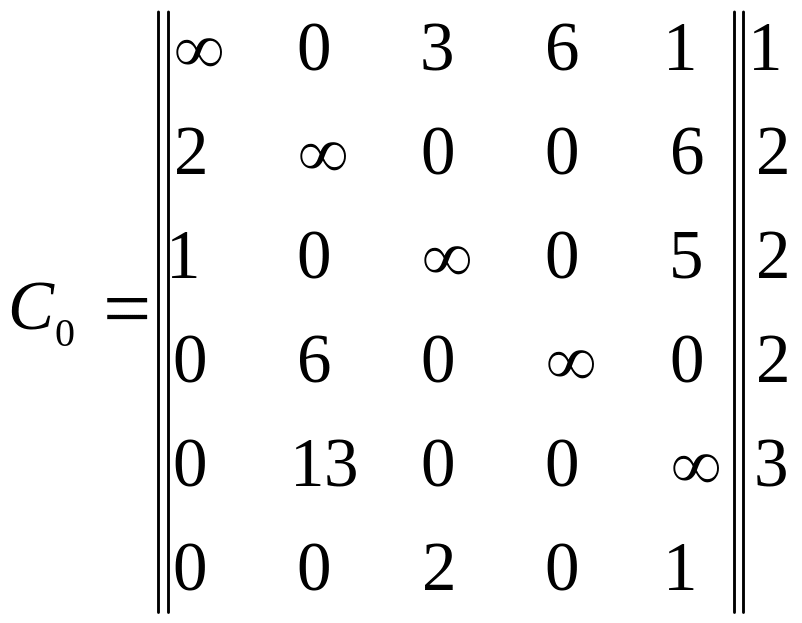
Шаг2. Вычисляем нижнюю оценку
Шаг
3. По образовавшимся нулевым элементам
в матрице пробуем составить цикл.
Получаем <1,2,3,4,5,1> следовательно
задача решена. Маршрут <1,2,3,4,5,1>
является оптимальным, а его длина
равна 13.
3.2 Ручная реализация алгоритма решения задачи с помощью метода полного перебора
На данном этапе необходимо выполнить ручной просчёт на основании данных, взятых из задания к курсовой работе. На данном этапе необходимо выполнить ручной просчёт на основании данных, взятых из задания к курсовой работе. В качестве примера для данного алгоритма мы приведем только несколько расчетов.
Исходная матрица:
А
А
А
А
А
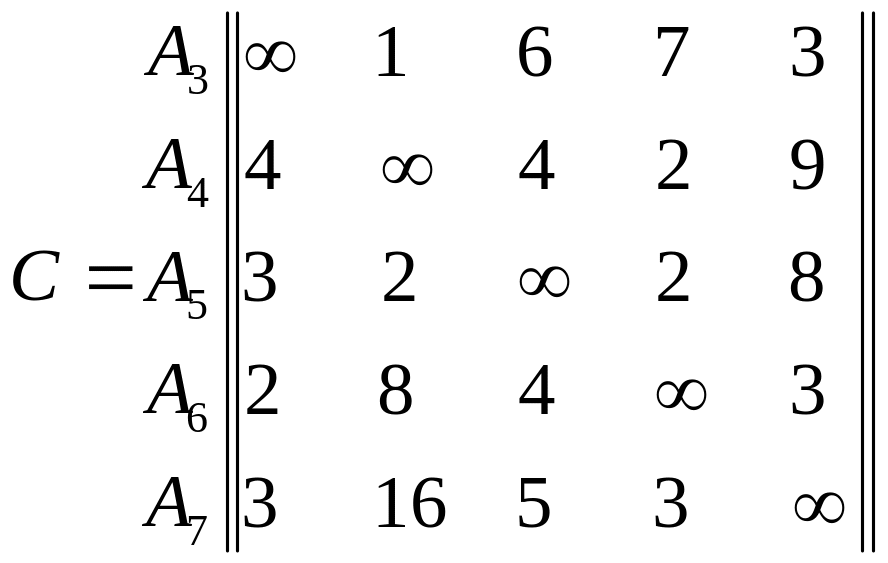
Н
а
промежутке от 0 до1 генератор автоматически
сам выбирает определенный промежуток,
который может быть различным. Допустим,
что генератор выбрал промежуток
.
Для дальнейшего решения нам необходимо
составить опорный план. Допустим
- является первым опорным планом.
{5,7,3,6,4}
{5,7,3,6,4}
(
)
= 8+3+7+8 = 26 
{3,7,5,6,4}
(
)
= 3+5+2+8= 18
{5,3,7,6,4}
(
)
= 3+3+3+8 = 17 
{7,3,5,6,4}
(
)
= 3+6+2+8 = 19
{7,5,3,6,4}
(
)
= 5+3+7+8 = 23 
{3,5,7,6,4}
(
)
= 6+8+3+8 = 25
В первом случае для решении мы не изменяем предпоследние и последнее число, а по всем остальным числам будет вестись пересчет. После всех расчетов мы выбираем наименьшую оценку и ее записываем для дальнейших расчетов. В данном случае наименьшей оценкой является выражение: {5,3,7,6,4} ( ) = 3+3+3+8 = 17
{5,3,7,6,4}
{5,3,7,6,4}
(
)
= 3+3+3+8 = 17 
{5,6,7,3,4}
(
)
= 2+3+3+1= 9
{5,3,6,7,4}
(
)
= 3+7+3+16 = 29 
{5,7,6,3,4}
(
)
= 8+3+2+1 = 14
{5,6,3,7,4}
(
)
= 2+2+3+16 = 23 
{5,7,3,6,4}
(
)
= 8+3+7+8 = 26
Во втором случае для решении мы не изменяем первое и последнее число, а по всем остальным числам будет вестись пересчет. В данном случае наименьшей оценкой является выражение: {5,6,7,3,4} ( ) = 2+3+3+1= 9
{5,6,7,3,4}
{5,6,7,3,4}
(
)
= 2+3+3+1= 9
{5,6,4,3,7}
(
)
= 2+8+4+3= 17
{5,6,7,4,3}
(
)
= 2+3+16+4 = 25 
{5,6,3,4,7}
(
)
= 2+2+1+9 = 14
{5,6,4,7,3}
(
)
= 2+8+9+3 = 22 
{5,6,3,7,4}
(
)
= 2+2+3+16 = 23
2 Случай
Допустим, что генератор выбрал промежуток
.
Для дальнейшего решения нам необходимо
составить 2 опорный план. Допустим
-
является второй опорным планом.
{3,6,4,7,5}
{3,6,4,7,5} ( ) = 7+8+9+5 = 29 {4,6,3,7,5} ( ) = 2+2+3+5= 12
{3,4,6,7,5} ( ) = 1+2+3+5 = 11 {6,4,3,7,5} ( ) = 8+4+3+5 = 20
{4,3,6,7,5} ( ) = 4+7+3+5 = 19 {6,3,4,7,5} ( ) = 2+1+9+5 = 25
В первом случае для решении мы не изменяем предпоследние и последнее число, а по всем остальным числам будет вестись пересчет. После всех расчетов мы выбираем наименьшую оценку и ее записываем для дальнейших расчетов. В данном случае наименьшей оценкой является выражение: {3,4,6,7,5} ( ) = 1+2+3+5 = 11
{3,4,6,7,5}
{3,4,6,7,5} ( ) = 1+2+3+5 = 11 {3,6,4,7,5} ( ) = 7+8+9+5= 29
{3,4,7,6,5} ( ) = 1+9+3+4 = 17 {3,7,6,4,5} ( ) = 3+3+8+4 = 18
{3,6,7,4,5} ( ) = 7+3+16+4 = 30 {3,7,4,6,5} ( ) = 3+16+2+4 = 25
Во втором случае для решении мы не изменяем, первое и последнее число, а по всем остальным числам будет вестись пересчет. В данном случае наименьшей оценкой является выражение: {3,4,6,7,5} ( ) = 1+2+3+5 = 11
{3,4,6,7,5}
{3,4,6,7,5} ( ) = 1+2+3+5 = 11 {3,4,5,7,6} ( ) = 1+4+8+3= 16
{3,4,6,5,7} ( ) = 1+2+4+8 = 15 {3,4,7,6,5} ( ) = 1+9+3+4 = 17
{3,4,5,6,7} ( ) = 1+4+2+3 = 10 {3,4,7,5,6} ( ) = 1+9+5+2 = 17
Для удобства расчетов составим таблицу, содержащую в первом столбце пути во втором сумму расстояний для этого пути, а в третьем длину получившегося пути.
1 2 3 4 5 |
3+ 1+ 4+ 2+ 3 |
13 |
1 2 3 5 4 |
2+ 1+ 4+ 8+ 3 |
18 |
1 2 4 3 5 |
3+ 1+ 2+ 4+ 8 |
18 |
1 2 4 5 3 |
3+ 1+ 2+ 3+ 5 |
14 |
1 2 5 3 4 |
2+ 1+ 9+ 5+ 2 |
19 |
1 2 5 4 3 |
3+ 1+ 9+ 3+ 4 |
20 |
1 3 2 4 5 |
3+ 6+ 2+ 2+ 3 |
16 |
1 3 2 5 4 |
2+ 6+ 2+ 9+ 3 |
22 |
1 3 4 2 5 |
3+ 6+ 2+ 8+ 9 |
28 |
1 3 4 5 2 |
4+ 6+ 2+ 3+ 16 |
31 |
1 3 5 2 4 |
2+ 6+ 8+ 16+ 2 |
34 |
1 3 5 4 2 |
4+ 6+ 8+ 3+ 8 |
29 |
1 4 2 3 5 |
3+ 7+ 8+ 4+ 8 |
30 |
1 4 2 5 3 |
3+ 7+ 8+ 9+ 5 |
32 |
1 4 3 2 5 |
3+ 7+ 4+ 2+ 9 |
25 |
1 4 3 5 2 |
4+ 7+ 4+ 8+ 16 |
39 |
1 4 5 2 3 |
3+ 7+ 3+ 16+ 4 |
33 |
1 4 5 3 2 |
4+ 7+ 3+ 5+ 2 |
21 |
1 5 2 3 4 |
2+ 3+ 16+ 4+ 2 |
27 |
1 5 2 4 3 |
3+ 3+ 16+ 2+ 4 |
28 |
1 5 3 2 4 |
2+ 3+ 5+ 2+ 2 |
14 |
1 5 3 4 2 |
4+ 3+ 5+ 2+ 8 |
22 |
1 5 4 2 3 |
3+ 3+ 3+ 8+ 4 |
21 |
1 5 4 3 2 |
4+ 3+ 3+ 4+ 2 |
16 |
2 1 3 4 5 |
16+ 4+ 6+ 2+ 3 |
31 |
2 1 3 5 4 |
8+ 4+ 6+ 8+ 3 |
29 |
2 1 4 3 5 |
16+ 4+ 7+ 4+ 8 |
39 |
2 1 4 5 3 |
2+ 4+ 7+ 3+ 5 |
21 |
2 1 5 3 4 |
8+ 4+ 3+ 5+ 2 |
22 |
2 1 5 4 3 |
2+ 4+ 3+ 3+ 4 |
16 |
2 3 1 4 5 |
16+ 4+ 3+ 7+ 3 |
33 |
2 3 1 5 4 |
8+ 4+ 3+ 3+ 3 |
21 |
2 3 4 1 5 |
16+ 4+ 2+ 2+ 3 |
27 |
2 3 4 5 1 |
1+ 4+ 2+ 3+ 3 |
13 |
2 3 5 1 4 |
8+ 4+ 8+ 3+ 7 |
30 |
2 3 5 4 1 |
1+ 4+ 8+ 3+ 2 |
18 |
2 4 1 3 5 |
16+ 2+ 2+ 6+ 8 |
34 |
2 4 1 5 3 |
2+ 2+ 2+ 3+ 5 |
14 |
2 4 3 1 5 |
16+ 2+ 4+ 3+ 3 |
28 |
2 4 3 5 1 |
1+ 2+ 4+ 8+ 3 |
18 |
2 4 5 1 3 |
2+ 2+ 3+ 3+ 6 |
16 |
2 4 5 3 1 |
1+ 2+ 3+ 5+ 3 |
14 |
2 5 1 3 4 |
8+ 9+ 3+ 6+ 2 |
28 |
2 5 1 4 3 |
2+ 9+ 3+ 7+ 4 |
25 |
2 5 3 1 4 |
8+ 9+ 5+ 3+ 7 |
32 |
2 5 3 4 1 |
1+ 9+ 5+ 2+ 2 |
19 |
2 5 4 1 3 |
2+ 9+ 3+ 2+ 6 |
22 |
2 5 4 3 1 |
1+ 9+ 3+ 4+ 3 |
20 |
3 1 2 4 5 |
5+ 3+ 1+ 2+ 3 |
14 |
3 1 2 5 4 |
4+ 3+ 1+ 9+ 3 |
20 |
3 1 4 2 5 |
5+ 3+ 7+ 8+ 9 |
32 |
3 1 4 5 2 |
4+ 3+ 7+ 3+ 16 |
33 |
3 1 5 2 4 |
4+ 3+ 3+ 16+ 2 |
28 |
3 1 5 4 2 |
4+ 3+ 3+ 3+ 8 |
21 |
3 2 1 4 5 |
5+ 2+ 4+ 7+ 3 |
21 |
3 2 1 5 4 |
4+ 2+ 4+ 3+ 3 |
16 |
3 2 4 1 5 |
5+ 2+ 2+ 2+ 3 |
14 |
3 2 4 5 1 |
6+ 2+ 2+ 3+ 3 |
16 |
3 2 5 1 4 |
4+ 2+ 9+ 3+ 7 |
25 |
3 2 5 4 1 |
6+ 2+ 9+ 3+ 2 |
22 |
3 4 1 2 5 |
5+ 2+ 2+ 1+ 9 |
19 |
3 4 1 5 2 |
4+ 2+ 2+ 3+ 16 |
27 |
3 4 2 1 5 |
5+ 2+ 8+ 4+ 3 |
22 |
3 4 2 5 1 |
6+ 2+ 8+ 9+ 3 |
28 |
3 4 5 1 2 |
4+ 2+ 3+ 3+ 1 |
13 |
3 4 5 2 1 |
6+ 2+ 3+ 16+ 4 |
31 |
3 5 1 2 4 |
4+ 8+ 3+ 1+ 2 |
18 |
3 5 1 4 2 |
4+ 8+ 3+ 7+ 8 |
30 |
3 5 2 1 4 |
4+ 8+ 16+ 4+ 7 |
39 |
3 5 2 4 1 |
6+ 8+ 16+ 2+ 2 |
34 |
3 5 4 1 2 |
4+ 8+ 3+ 2+ 1 |
18 |
3 5 4 2 1 |
6+ 8+ 3+ 8+ 4 |
29 |
4 1 2 3 5 |
3+ 2+ 1+ 4+ 8 |
18 |
4 1 2 5 3 |
2+ 2+ 1+ 9+ 5 |
19 |
4 1 3 2 5 |
3+ 2+ 6+ 2+ 9 |
22 |
4 1 3 5 2 |
2+ 2+ 6+ 8+ 16 |
34 |
4 1 5 2 3 |
2+ 2+ 3+ 16+ 4 |
27 |
4 1 5 3 2 |
2+ 2+ 3+ 5+ 2 |
14 |
4 2 1 3 5 |
3+ 8+ 4+ 6+ 8 |
29 |
4 2 1 5 3 |
2+ 8+ 4+ 3+ 5 |
22 |
4 2 3 1 5 |
3+ 8+ 4+ 3+ 3 |
21 |
4 2 3 5 1 |
7+ 8+ 4+ 8+ 3 |
30 |
4 2 5 1 3 |
2+ 8+ 9+ 3+ 6 |
28 |
4 2 5 3 1 |
7+ 8+ 9+ 5+ 3 |
32 |
4 3 1 2 5 |
3+ 4+ 3+ 1+ 9 |
20 |
4 3 1 5 2 |
2+ 4+ 3+ 3+ 16 |
28 |
4 3 2 1 5 |
3+ 4+ 2+ 4+ 3 |
16 |
4 3 2 5 1 |
7+ 4+ 2+ 9+ 3 |
25 |
4 3 5 1 2 |
2+ 4+ 8+ 3+ 1 |
18 |
4 3 5 2 1 |
7+ 4+ 8+ 16+ 4 |
39 |
4 5 1 2 3 |
2+ 3+ 3+ 1+ 4 |
13 |
4 5 1 3 2 |
2+ 3+ 3+ 6+ 2 |
16 |
4 5 2 1 3 |
2+ 3+ 16+ 4+ 6 |
31 |
4 5 2 3 1 |
7+ 3+ 16+ 4+ 3 |
33 |
4 5 3 1 2 |
2+ 3+ 5+ 3+ 1 |
14 |
4 5 3 2 1 |
7+ 3+ 5+ 2+ 4 |
21 |
5 1 2 3 4 |
3+ 3+ 1+ 4+ 2 |
13 |
5 1 2 4 3 |
8+ 3+ 1+ 2+ 4 |
18 |
5 1 3 2 4 |
3+ 3+ 6+ 2+ 2 |
16 |
5 1 3 4 2 |
9+ 3+ 6+ 2+ 8 |
28 |
5 1 4 2 3 |
8+ 3+ 7+ 8+ 4 |
30 |
5 1 4 3 2 |
9+ 3+ 7+ 4+ 2 |
25 |
5 2 1 3 4 |
3+ 16+ 4+ 6+ 2 |
31 |
5 2 1 4 3 |
8+ 16+ 4+ 7+ 4 |
39 |
5 2 3 1 4 |
3+ 16+ 4+ 3+ 7 |
33 |
5 2 3 4 1 |
3+ 16+ 4+ 2+ 2 |
27 |
5 2 4 1 3 |
8+ 16+ 2+ 2+ 6 |
34 |
5 2 4 3 1 |
3+ 16+ 2+ 4+ 3 |
28 |
5 3 1 2 4 |
3+ 5+ 3+ 1+ 2 |
14 |
5 3 1 4 2 |
9+ 5+ 3+ 7+ 8 |
32 |
5 3 2 1 4 |
3+ 5+ 2+ 4+ 7 |
21 |
5 3 2 4 1 |
3+ 5+ 2+ 2+ 2 |
14 |
5 3 4 1 2 |
9+ 5+ 2+ 2+ 1 |
19 |
5 3 4 2 1 |
3+ 5+ 2+ 8+ 4 |
22 |
5 4 1 2 3 |
8+ 3+ 2+ 1+ 4 |
18 |
5 4 1 3 2 |
9+ 3+ 2+ 6+ 2 |
22 |
5 4 2 1 3 |
8+ 3+ 8+ 4+ 6 |
29 |
5 4 2 3 1 |
3+ 3+ 8+ 4+ 3 |
21 |
5 4 3 1 2 |
9+ 3+ 4+ 3+ 1 |
20 |
5 4 3 2 1 |
3+ 3+ 4+ 2+ 4 |
16 |
Просмотрев таблицу, находим в ней строку с минимальным значением третьего столбца. В нашем случае таких строк 5:
1 2 3 4 5 |
3+ 1+ 4+ 2+ 3 |
13 |
2 3 4 5 1 |
1+ 4+ 2+ 3+ 3 |
13 |
3 4 5 1 2 |
4+ 2+ 3+ 3+ 1 |
13 |
4 5 1 2 3 |
2+ 3+ 3+ 1+ 4 |
13 |
5 1 2 3 4 |
3+ 3+ 1+ 4+ 2 |
13 |
Но все они фактически являются одним и тем же путем только с разным начальным городом т.к. если их прокрутить, то они станут одинаковыми.
Значит, маршрут <1,2,3,4,5,1> является оптимальным, а его длина равна 13.