12 Октября 2011.

Тема: Погрешности измерений.

Результат измерений всегда содержит погрешность. Значение этой погрешности является целью теории и практики обработки результата измерений.

Погрешность измерений всегда заключает в себя ряд составляющих:

• По закономерности проявления:

  • Систематическая – это составляющая погрешности, сохраняющая постоянное значения и знак, или проявляющая определенную закономерность при повторных измерениях одного и того же значения физической величины;

  • Случайная – составляющая погрешности, получаемая случайным образом при повторном измерении одного и того же значения физической величины;

  • Промах – грубое искажение результата измерения вследствие небрежности или низкой квалификации оператора, а также неожиданных внешних факторов.

• По источникам возникновения:

  • Методические, которые возникают от несовершенства метода измерения, использования упрощающих допущений, неполноты знаний о проходящих методических процессах;

  • Инструментальные, причины которых – неточности градуировки, допуски на деталях, конструктивные несовершенства и изменения характеристик в процессе эксплуатации;

  • Субъективные, обусловленные индивидуальными особенностями предмета.

• В зависимости от способа представления:

  • Абсолютная

  • Относительная

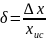
Погрешность состоит из случайной и систематической составляющей: и в общем виде является случайной величиной. Каждая СВ полностью характеризуется ее распределением. Применительно к погрешности это распределение определяет вероятность того, что СВ в i-том наблюдении окажется меньше некоторого заданного значения.

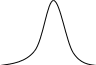
Чаще используют не распределение вероятности, а функция плотности распределения:

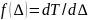
F

∆

f(∆)

∆

Вероятность нахождения будет определяться площадью под этой кривой:

, где a и b – квантили распределения. Соответственно систематическая погрешность выражена следующим образом: 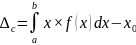, где x₀ – отклонение математического ожидания от истинного значения:

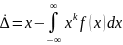
k=1, тогда М[X]=∫xf(x)dx - математическое ожидание.

Фактически математические ожидание является оценкой истинного значения изменяемой величины.

Центральный момент:

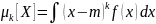
– дисперсии (D). Дисперсия характеризует разброс.

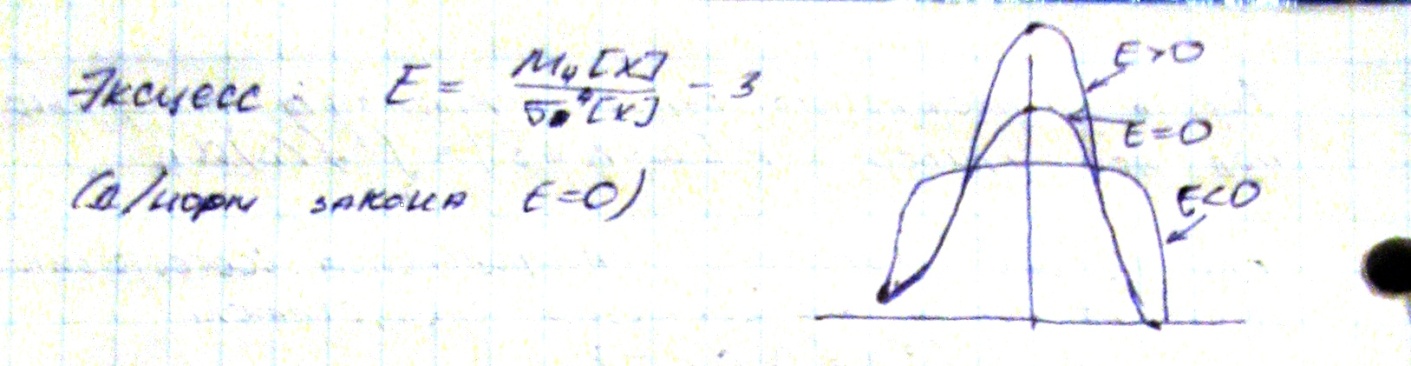
В теории обработки результатов используют нормальный закон распределения.

Распределение Вейбула (используется в теории надежности).

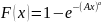
При α=1 распределение становится показательным; α=2 репеевское распределение; α=3.3 – близкое к нормальному.

Равномерный закон распределения – используется при измерении непрерывных величин методом дискретного счета. Его так же используют для оценки неисключенной систематической погрешности. Если отсутствуют данные о распределении систематической погрешности, так как результат измерения оценивается пределами допускаемой погрешности.

19 Октября 2011.

Тема: Оценка погрешности измерений.

Измерение считается правильным, если систематическая погрешность равно нулю, поэтому учет и исключение систематической погрешности является главной задачей планирования эксперимента.

Систематические погрешности:

1. Постоянные;

2. Прогрессирующие;

3. Периодические.

На практике возможны следующие случаи:

1. Реальные условия позволяют устранить источники систематической погрешности до начала измерений. При этом применяются следующие способы:

   1. Установка нулей;

   2. Предварительная поверка, калибровка – необходимо убедиться что аппаратура исправна;

   3. Термостатирование – уменьшение колебания температуры;

   4. Экранировка – защита от электромагнитных полей;

   5. Виброзащита;

   6. Подготовка рабочего места.(протирая влажной тряпкой можно убрать статический заряд).

2. Происхождение систематической погрешности известно, ее значение может быть определено, обычно оно указывается в свидетельстве о поверке. В таких случаях вводят поправку. Поправка – величина объекта с систематической погрешностью, добавление которой исключает эту погрешность.

3. Причина систематической погрешности ясна из физических соображений, но ее значение неизвестно. Существует ряд способов уменьшения:

   1. Если погрешность постоянная, то применяют методы замещения, противопоставления и компенсации погрешности по знаку. При методе замещения проводят 2 наблюдения. ВО втором наблюдении источник сигнала заменяют мерой или заведомо исправным устройством с хорошо известными характеристиками. Расхождение значения в двух наблюдениях дает значение систематической погрешности, которое учитывается путем введения поправок. В методе противопоставления проводят четное количество наблюдений, в которых причина погрешности может оказывать хорошо известное воздействие на результат измерения. То есть устанавливается вид систематической погрешности. Метод компенсации по знаку предусматривает наблюдение с двумя измерениями, результат которых находят в виде полусуммы.

   2. Существенное уменьшение систематической погрешности может дать рандомизация, или перевод систематической погрешности в случайную. Наиболее распространенный прием рандомизации: измерение проводится несколькими однотипными приборами, результат измерения определяется статистической обработкой каждого измерения.

Д

Х

Х2

Х1

ля обнаружения прогрессирующих систематических погрешностей используется графический метод и наличие изменяющихся функций свидетельствует о наличии систематических погрешностей. Если погрешность линейна, то для исключения такой погрешности используют метод симметричных наблюдений. При данном методе все можно свести к двум наблюдениям.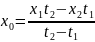

t1 t2 t

4. О систематической погрешности ничего не известно, хотя он присутствует. Результаты изменений могут вызвать серьезные заблуждения. В таких случаях надежной методикой можно считать измерение величины основанным на другом явлении, однако возникает вопрос, какой из двух выводов является правильным. Этот метод часто невозможно применять, так как данный метод единственный возможный. Однако техника позволяет воспользоваться путем численного моделирования процедуры измерения.

Однако систематические погрешности невозможно полностью исключить, всегда остаются неисключенные, которые рассматриваются как случайные, и определяют доверительные границы. При этом руководствуются:

1. Если случайные погрешности малы, то границы НСП считают пределы основной погрешности СИ;

2. Проводя суммирование НСП, погрешности рассматриваются как случайные, причем в отсутствии сведений о виде распределения принимают равномерное;

3. Если НСП обусловлено несколькими источниками, то доверительные границы вычисляют на основе композиции отдельных погрешностей. При равномерном распределении суммарная погрешность берется как среднее геометрическое: 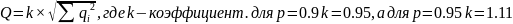. При вычислении границ НСП, при наличии случайной погрешности доверительная вероятность принимают такой же как при вычислении доверительных границ случайной погрешности.

Существуют измерения с многократными и однократными наблюдениями.

Измерения с многократными наблюдениями, у которых число измерений больше или равно 4. При обработке результатов с многократными наблюдениями вычисляют от точной оценки, у которой является СКО наблюдений, СКО результатов, среднее арифметическое. Границы доверительного интервала являются так же СВ. Для определения погрешности используют распределение φ², которые обеспечивают достоверность до двух значащих цифр с точностью до 5%. На практике такая точность определения погрешности излишня, поэтому существуют правила округления результата измерения.

Порядок округления:

1. Погрешность округляют до первой значащей цифры;

2. Результат округляется до порядка значащей цифры, но существуют случаи, когда погрешность измерения больше первой значащей цифры, то допускается вторая значащая цифра.

Однократные измерения проводятся тогда, кода значения измеряемой величины не изменяются в течении длительного времени. Такое возможно, если:

1. Объем априорной информации такой, что модель объекта и измеряемая величины не вызывают сомнения;

2. Метод достаточно изучен и его погрешность хорошо известна и устранена;

3. СИ исправно, их метрологические характеристики соответствуют установленным нормам.

Результатом однократного измерения является показания прибора, погрешность измерений является систематической и сумма из основной и дополнительной погрешности СИ есть сумма методической и субъективной погрешности. В простейшем случае погрешность измерений принимается равной пределу основной погрешности. При этом результат измерения может быть записан без указания доверительной вероятности, которую принимают равной 1.

При наличии нескольких систематических погрешностей их суммарное значение находят в виде геометрической суммы, однако в случае, когда результаты важны для здоровья людей, предотвращения катастроф, то берется сумма без учета знака, однако в этом случае могут быть абсурдные результаты.

При косвенных измерениях измеряемая величина А является функцией многих переменных А=А(х1, х2…, хn) и соответственно можно считать, что суммарная погрешность – функция всех погрешностей ее составляющих.

Относительная погрешность:

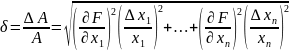
Отсюда следует, что относительная погрешность произведения или деления двух величин будут иметь одинаковую погрешность, определяемую выражением:

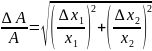
А=Х1*Х2; А=Х2/Х1; А=Х1/Х2.

Из этого выражения возникает правило критерия ничтожно малой погрешности – если имеются две составляющие погрешности, одна из которых в 3 раза меньше другой, то наименьшей можно пренебречь.