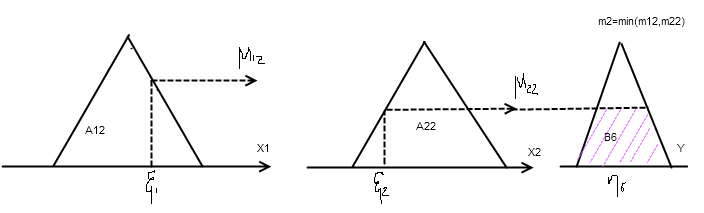
Процесс преобразования значений входных переменных х1 и х2 в выходную у.

Пусть каждая из входных переменных имеет 5 термов, а выходная переменная, являющаяся управляющим воздействием, 7 термов.

Пусть входные переменные х₁=ξ₁, а х₂=ξ₂. Процедуру преобразования поясним на примере действия двух правил:

1. ЕСЛИ И ТО

2. ЕСЛИ И ТО

На этапе позификации входные физические переменные преобразуются в соответствующие термы. Для рассматриваемого примера значение х₁=ξ₁, а х₂=ξ₂ измеренные в некоторый момент времени определяют два значения ФП термов А₁₂, А₂₂.

1. µ₁₂=0.7 µ₂₂=0.4

2. µ₁₁=0.73 µ₂₂=0.4

На этапе логического заключения выходным термом переменной у присваивается значение ФП входных переменных с общим условием µ(у)≤µ(х) и конкретно для правил с оператором «И» согласно принципу минимума.

В результате выходные термы В₆=РМ и В₇=РВ оказываются усеченными минимальными значениями входных функций принадлежности. Полученные по двум активизированным правилам термы В₆ и В₇ объединяются по принципу максимума (оператор «ИЛИ») в один общий терм В=В₆ Ѵ В₇. Полученный результирующий терм В определяет множество возможных значений управляющего воздействия у. Преобразование входных термов в выходные с передачей от входа к выходу значений функций принадлежности по принципу минимума-максимума получило название min-max регулятор Мамдани.

1. ЕСЛИ И

2. ЕСЛИ И

Вопрос как выбрать одно конкретное значение η для физической выходной переменной решается на третьем этапе преобразования – дефазификации.

Лекция 5 (02.11.2013)

На этом этапе логическая переменная должна быть преобразована в определенное значение физической переменной – управляющее воздействие. Для интегральной оценки одним числом всего множества значений в fuzzy-логике за это число принимают абсциссу центра тяжести площади усеченной части терма.

Расчет производится по формуле:

Данный метод для расчета значения оказывается сложным, поскольку требует много места в тетради. На практике используют его достаточно несложную модификацию в виде, так называемых, … функции:

Кроме рассмотренной системы Мамдани, существует нечеткая система Сугэно. Если в системе Мамдани база знаний состоит из правил вида:

ЕСЛИ х₁ – низкий И х₂ – средний ТО у=а₀+а₁х₁+а₂х₂

То основное различие между системами Мамдани и Сигуна, заключается в разных способах задания значений выходной переменной в правилах, образующих базу знаний.

В системах типа Мамдани, значения выходной переменной задаются нечеткими термами, в системе типа Сугэна, как линейная комбинация входных переменных.

Fuzzy-управление, в принципе, не требует знаний точной модели объекта тогда, когда необходимый алгоритм управления возможно сформулировать лингвистическим путем, а в тех областях, где возможно и фаззи и традиционное управление, предпочтение отдается способу, который дает лучший результат по требуемому показателю.

Лекция 3 (12.10.2013)

Control System Toolbox (CST)

CST предназначен для моделирования, анализа и проектирования САУ как непрерывных, так и дискретных. Модели CST могут быть одномерными и многомерными (SISO, MIMO).CST модели могут быть представлены в следующем виде: tf-форма, zpk-форма, ss-форма, dss-форма, fzd-форма.

Ss-модель (StateSpace) – модель в пространстве состояний, которая представляет ДУ в нормальной форме Коши, которая дополняется алгебраическими уравнениями, связывающие выходные переменные с переменными состояниями.

Где u – вектор входных переменных, y – вектор выходных переменных, x– вектор переменных состояний; А – матрица состояния, В – матрица входных воздействий, С – матрица выходных воздействий, D – матрица проходная.

B

D

∫

C

u

x

y

x

Задание этой модели в командной строке происходит следующим образом:

Sys=ss ([A], [B], [C], [D])

Tf (transferFunction) передаточная функция, задается многочленом в числителе и многочленом в знаменателе.

h= tf ([num], [den])

Структурная схема САУ может быть построена в CST с помощью функций соединения LTI модели. Представим эти функции в таблице.

Parallel	Параллельное соединение (сложение lti-моделей)
Series	Последовательное соединение (умножение lti-моделей)
Feedback	Соединение с ОС
Append	Объединение lti-моделей с добавлением входов и выходов
Connect	Объединение моделей с использованием матрицы соединений
Star	Объединение взаимосвязанных многомерных моделей

1. Параллельное соединение моделей

Sys=parallel(sys1, sys2)=parallel(sys1, sys2, in1, in2, out1, out2)

Эта функция эквивалентна операции сложения lti-моделью

2. Последовательное соединение

Sys=series(sys1, sys2)=series(sys1, sys2, out1, in2)

Эта функция эквивалентна операции умножения lti-моделей sys=sys₁*sys₂

3. Соединение lti-моделей с ОС

Sys=feedback(sys1, sys2, sign)

Где

4. Объединение моделей с помощью функции append и матрицы связей Q. Функция append позволяет объединить разрозненные модели в одну многомерную.

Sys=append(sys1, sys2, …, sysN)

Матрица связей Q предназначена для описания связей блоков на структурной схеме. Каждая строка этой матрицы соответствует одному входу системы sys. Первый элемент строки – это номер входа, последующие элементы указывают номера выходов, которые алгебраически суммируются по этому входу. Отрицательные элементы обозначают суммирование со знаком «-».

Пример. Необходимо для заданной структурной схемы в виде переменных передаточной функции построить ее одномерную модель.

Возможны два варианта решения задачи:

1. С использованием операторов series, feedback

2. С использованием операторов append, connect

1. Вводим в CST параметры звеньев s₁, s₂:

Объединим звенья s₁ и s₂:

Составим матрицу соединения звеньев:

Зададим вход и выход агрегированной модели:

Выполним соединение звеньев:

Исследуем:

2. Получим передаточную функцию последовательного соединения:

Получим передаточную функцию с учетом ООС:

Исследуем:

Лекция 5 (02.11.2013)

Функции преобразования дискретных моделей в непрерывные в CST (Control System Toolbox)

Очень часто при проектировании САУ возникает необходимость получения дискретных моделей непрерывных систем, при выполнении этого преобразования требуется обеспечить эквивалентность систем. Эквивалентность понимается в том смысле, что при соответствующих начальных условиях, их реакции на одно и тоже воздействие должно совпадать. Погрешность в преобразовании вносит дискретизации по времени и квантование по уровню. Дискретизация сигналов по времени делает систему дискретной, а квантование по уровню – нелинейной. Оба процесса сопровождаются возникновением методических погрешностей. Выбор частоты дискретизации производится исходя из ширины полосы пропускания или из времени регулирования замкнутой системы. У разомкнутой системы, частоты дискретизации в 6-10 раз больше полосы пропускания или от 2 до 4 дискретных отсчетов за время нарастания. В противном случает качество системы будет резко ухудшаться.

Однако при увеличении частоты квантовании более чем в 2 раза по сравнению с верхнпей частотой спектра сигнала (по теореме Котельникова) дальнейшего увеличения качества регулирования не происходит. Определение целесообразного значения шага может быть найдено так же по формуле из методички Шалобанова.

К_рс – коэффициент передачи разомкнутой системы, T_min – наименьшая из постоянных времени апериодических звеньев, входящих в соответствующую систему.

Количество ступеней квантования оказывает существенное влияние на динамические свойства системы.

В состав CST включено две функции для преобразования непрерывных моделей в дискретные и дискретные в непрерывные: c2d, d2c.

Метод экстраполяции	Описание метода	наличие в simulink
zero-order hold	экстраполяция нулевого порядка	+
first-order hold	экстраполяция первого порядка	+
tustin	биполярна аппроксимация Тастина	-
prewarp	аппроксимация Тастина с коррекцией	-
matched	метод соответствия нулей и полюсов	-

sysD=c2d(sysC,Ts,’метод’) – реализует построение дискретной модели sysD непрерывной модели sysС с периодом дискретизации Ts и с использование одного из вышеперечисленных методом экстраполяции. Если метод не указан, то по умолчанию используется экстраполяция нулевого порядка (ZOH).