Российский государственный торгово-экономический университет

Кафедра Информационных технологий и телекоммуникаций

Коровина Л.И.

Методические указания к практическим занятиям

По дисциплине "Математическая экономика"

На практических занятиях и в самостоятельной работе над курсом студентам рекомендуется пользоваться нижеприведёнными методическими указаниями и практическими приёмами выполнения тех заданий, которые, как предполагается, должны выполняться с помощью электронных таблиц Microsoft Excel и пакетов Mathcad , Maple и Statistica в компьютерных классах ПК.

Предполагается, что все практические занятия проводятся в компьютерных классах и каждый студент работает за отдельным компьютером.

Результаты работы должны быть сохранены на отдельном носителе до зачёта или экзамена.

При защите каждой задачи студент должен проявить следующие знания и умения:

• уметь формулировать постановку экономической задачи,

• связно излагать процесс построение математической модели,

• осознавать условия применимости математической модели,

• грамотно анализировать полученные результаты,

• правильно отвечать на контрольные вопросы о методах решения задачи и об используемых при этом информационных технологиях.

Занятие №1

Тема задания. Нелинейные уравнения в моделировании экономических процессов и методы их решения. (4 часа).

Содержание задания.

Аналитические и численные методы решения нелинейных уравнений. Решение нелинейных уравнений в пакетах Mathcad, Maple.

Задача 1. Постройте графики зависимости спроса от дохода для малоценных товаров D₀(x), товаров первой необходимости D₁(x), товаров второй необходимости D₂(x), и для предметов роскоши D₃(x), используя математическую модель, предложенную шведским ученым Торнквистом. Исследуйте также изменение вида кривых при изменении параметров α, β, γ.

Пусть α =15, β =5, γ=10.

1. D₀(x) = (α*х)* (x+β)/( х²+ γ) .

К какому предельному значению стремится спрос D₀(x) при неограниченном увеличении дохода x ?

2. D₁(x) = (α*х)/(x+β) .

Определите графически, при каких значениях дохода х значения спроса D₁(x) начинают отличаться от предельного значения меньше, чем на 3 ?

3. D₂(x) = [α *(х- γ)]/( x+ β) .

Определите графически, при каких значениях дохода х значения спроса D₂(x) превышают значение 12.

4. D₃(x) = [α*x* (х- γ)]/( x+ β) .

Существует ли предел возрастания спроса при увеличении дохода в этом случае?

(Можно рассмотреть также варианты заданий из задачи 3.19, стр.603 [2]).

Рекомендации к решению. Решение задачи 2 выполняется аналогично приведенному на стр. 211 - 213 учебника [2].

О пределим исследуемые функции.

построения функций зададим, например, следующим образом: 0<x<100, 0<D<30.

Чтобы построить несколько графиков в одной и той же системе координат, вводите имена функций по оси ординат через запятую.

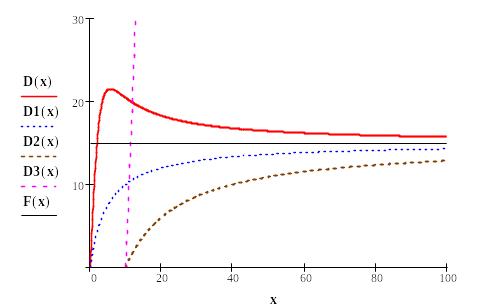
Проанализируем графики.

Спрос на малоценные товары растёт при малых доходах, затем достигает максимума и при дальнейшем увеличении дохода убывает, приближаясь асимптотически к величине сверху.

Спрос на товары первой необходимости растёт с ростом дохода, стремясь к величине  снизу.

Товары второй необходимости и предметы роскоши приобретаются только при доходах свыше Причем, спрос на товары второй необходимости ограничен сверху величиной  , а на товары роскоши растет неограниченно с ростом доходов.

Задача 1.2. Постройте график заданной функции спроса на малоценные товары в зависимости от дохода x : . Исследуйте вид кривой при разных значениях параметров , , .

Решение задачи.

Пусть вначале меняется при постоянных , =5 Выполним присвоения в рабочей области и построим графики.

Теперь пусть меняется при постоянных , . Зададим присвоения в рабочей области.

Теперь пусть меняется при постоянных , = 4 .

Зададим присвоения в рабочей области и построим графики.

А нализ графиков выполните самостоятельно.

Задача 2 . Постройте в среде Mathcad кривые спроса D(Q) = -AQ + B и предложения S(Q) = Q²/C + Q/d + E .

Найдите графически приближенно и затем численно с заданной точностью e=0.01 равновесную цену товара.

Исследуйте обусловленность вычислительной задачи..

Варианты значений констант A,B,C, d, E индивидуальных заданий можно взять из задачи 3.18, стр.603 [2] или задать по формулам:

A= (11*N)/(N+2) , где N - номер варианта,

B=110 , C=5 , d=3 , E=80.

Пример решения задачи при A=4 , B=120 , C=4 , d=2 , E=80.

Построим графики функций спроса и предложения, найдём количество товара Qравн, при котором достигается равновесная цена, и определим значение равновесной цены товара P.

Определяем в рабочей области функции и строим их графики.

A:=4 B:=120 C:=4 d:=2 E:=80.

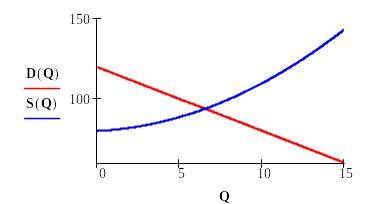
1. Графическим способом найдём значения

Qравн=6.51 ; P=93.96

_{Для этого один раз щёлкните левой клавишей мыши (ЛМ) по области графика, появятся маркеры и подключится графический редактор. Кликните один раз правой клавишей мыши (ПМ) по области графика. Появится меню. Выберите команду trace. Подведите курсор в виде стрелки к точке пересечения кривых и щёлкните ЛМ. В диалоговом окне высветятся значения координат точки пересечения.}

2. Уточним значения, найденные графическим способом,

с помощью вычислительного блока (Given...Find).

ОТВЕТ. Графическим способом найдены значения Q=6.51 ; P=93.96 .

Уточнённые данные: Q=6.52, P=93.90 ( все знаки верные).

Замечание. При решении задачи можно воспользоваться также рекомендованной литературой - стр. 210 - 211 учебника [2].

Указание. При исследовании обусловленности задачи варьируйте наименьший по модулю козффициент. Используйте относительные погрешности.