Задание № 6 оформление научной документации

1 Постановка задачи

1. Составьте макет научной статьи объемом до 2 страниц. В нее включите:

• И.О.Ф. автора;

• заголовок статьи;

• 7-10 строк формул;

• рисунок или график, или диаграмму;

• текст;

• список литературы.

2. Организуйте обтекание рисунка (графика, диаграммы) текстом.

3. Сделайте сноску на первой странице документа.

4. Проведите форматирование документа, в том числе выделите И.О.Ф. автора, название статьи.

5. Сохраните документ.

Образец макета научной статьи метод обработки опытных данных и.С. Иванов, а.М. Светляков

Предположим, что в результате серии экспериментов получена таблица некоторой зависимости от :

			….
			…

Надо найти формулу, выражающую эту зависимость аналитически

(4.1)

Строгая функциональная зависимость для экспериментально полученной таблицы наблюдается редко, т.к. каждая из величин и может зависеть от многих случайных факторов. Однако если удастся найти , то во-первых, она позволит найти значение для не табличных значений , «сглаживая» результаты измерений величины , во-вторых, позволит экстраполировать функциональную зависимость, т.е. найти , который соответствует некоторому , лежащему вне области эксперимента.

З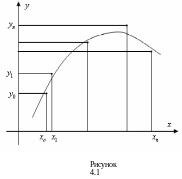 адача: найти зависимость , значения которой в точках мало отличается от опытных данных. Эта зависимость, полученная на основе опытных данных, называется эмпирической¹. Задача построения эмпирической формулы отличается от задачи интерполирования. График эмпирической зависимости не проходит через заданные точки , как в случае интерполяции. Это приводит к тому, что экспериментальные данные в некоторой степени «сглаживаются», а интерполяционная формула повторяла бы все ошибки, имеющиеся в данных. Построение эмпирической формулы состоит из двух этапов:

1) побора общего вида этой формулы,

2) определение наилучших значений, содержащихся в ней параметров.

Для выполнения первого этапа строится по таблице точечный график, затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек (см. рис. 4.1). По полученной таким образом кривой устанавливается вид приближающей функции.

Будем считать, что вид эмпирической формулы выбран:

, (4.2)

где – неизвестные постоянные параметры.

Обозначим разность между опытными данными и значениями эмпирической функции в точках через:

, (4.3)

где .

Теперь задача нахождения параметров сводится к минимизации отклонений .

Итак, согласно методу наименьших квадратов, параметры функции надо выбирать таким образом, чтобы сумма квадратов отклонений была наименьшей.

Определим функцию:

, (4.4)

теперь задача сводится к отысканию ее минимума. Здесь выступают в роли независимых переменных функции . Минимум найдем приравнивая нулю частные производные по этим переменным: , получим систему уравнений для определения .

Рассмотрим метод наименьших квадратов для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим многочлен , тогда . Найдем частные производные:

.

Приравнивая их к нулю и собирая коэффициенты при неизвестных , получим систему линейных уравнений:

(4.5)

Решая эту систему относительно неизвестных параметров , получим конкретный вид искомой функции .

Метод наименьших квадратов можно применять и к другим функциональным зависимостям, а не только к многочленам.