Тестовые задания по физике

Тема I (кинематика).

I – 1. Система отсчета – это

1. математические операции, позволяющие связать пространство и время;

2. система координат, связанная с взаимно неподвижными телами, дополненная способом измерения времени;

3. комплекс приборов, отсчитывающих время и расстояние;

4. системный блок в компьютере, позволяющий регистрировать пространственно временные характеристики.

I – 2. Радиус-вектор – это

1. радиус кривизны траектории;

2. вектор, направленный в сторону движения материальной точки;

3. вектор, проведенный из начала координат к материальной точке;

4. вектор, проведенный от материальной точки к началу координат.

I – 3. Путь – это

1. ;

2. длина радиуса-вектора;

3. изменение радиуса-вектора за время ;

4. расстояние, пройденное телом по траектории.

I – 4. Перемещение – это

1. скорость;

2. изменение радиуса-вектора;

3. расстояние, пройденное материальной точкой по траектории;

4. расстояние от начала координат до материальной точки.

I – 5. Если радиус-вектор равен , то в момент его модуль

равен

1) 10 м, 2) 5 м, 3) 14 м, 4) 2 м.

I – 6. Если радиус-вектор равен, то уравнением траектории

будет формула

1) , 2) , 3) , 4) .

I – 7. Если – путь, а – радиус-вектор, то для вектора мгновенной скорости

справедливо выражение

1) , 2) , 3) , 4) .

I – 8. Производная равна

1. средней скорости;

2. модулю вектора скорости;

3. перемещению;

4. вектору мгновенной скорости.

I – 9. Если и – зависящие от времени вектора ускорения и скорости, то

путь связан с промежутком времени формулой

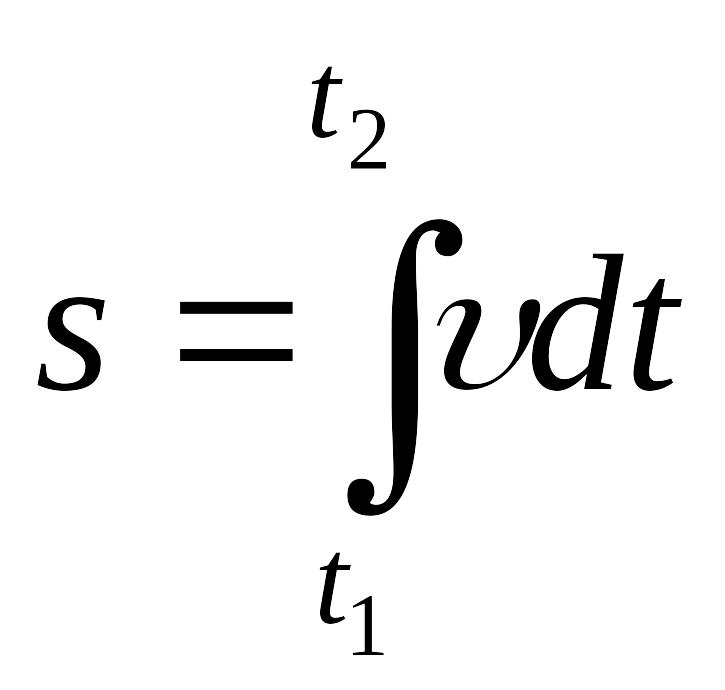1) , 2) , 3) , 4) .

I – 10. Радиус-вектор и скорость связаны между собой соотношением

1) , 2) , 3) , 4) .

I – 11. Интеграл равен (если )

1. пройденному за пути;

2. изменению скорости за ;

3. средней за скорости;

4. перемещению за .

I – 12. Если в момент времени t = 0 материальная точка начала движения со

скоростью , то зависимость координаты х от времени

выражается формулой

1) 3t, 2) , 3) , 4) 5 t.

I – 13. Производная равна

1. модулю полного ускорения;

2. модулю тангенциального ускорения;

3. модулю нормального ускорения;

4. полному ускорению.

I –14. Вектор полного ускорения в общем случае может быть найден

следующим образом

1) , 2) , 3) , 4) .

I – 15. Нормальное ускорение – это

1. правильно сосчитанное ускорение;

2. вектор ускорения;

3. скорость изменения направления скорости;

4. скорость изменения модуля скорости.

I – 16. Какое из этих соотношений справедливо? ( и – вектора ускорения

и скорости, R – радиус кривизны, и – тангенциальная и

нормальная составляющие ускорения.)

1) , 2) , 3) , 4) .

I – 17. Угловая скорость связана с углом поворота соотношением

1) , 2) , 3) , 4) .

I – 18. Если известна зависимость углового ускорения от времени , то

угловую скорость можно найти следующим образом:

1) , 2) , 3) , 4) .

I – 19. Поступательная скорость и угловая скорость связаны между собой равенством

1) ; 2) ; 3) ; 4) .

I – 20. Если – вектор углового ускорения, – радиус-вектор, то векторное

произведение равно

1. вектору полного ускорения;

2. вектору скорости;

3. вектору нормального ускорения;

4. вектору тангенциального ускорения.

I – 21. Если – вектор угловой скорости, – вектор скорости, то векторное

произведение равно

1. вектору углового ускорения;

2. вектору полного ускорения;

3. вектору нормального ускорения;

4. вектору тангенциального ускорения.

I – 22. Если вектор скорости равен , то модуль полного ускорения при t = 1 с равен

1) 7 м/с²; 2) 1 м/с²; 3) 5 м/с²; 4) м/с².

I – 23. Если вектор скорости равен , то тангенциальное ускорение при t = 2с равно

1) 5; 2)10 м/с²; 3) 20 м/с²; 4) 14 м/с².