Розрахунки абсолютного приросту

Абсолютний приріст, ∆Y
базисний	ланцюговий
-	-
2251	2251
2799	548
3090	291
3466	376
5548	2082
5582	34
6097	515
6117	20
6954	837
7313	359
8745	1432
8844	99
9186	342
9260	74
9614	354
10602	988
10677	75
13216	2539
13540	324

Розраховується:

∆Y_баз=Y_i-Y₁;

∆Y_ланц=Y_i-Y_i-1.

Таблиця 4.3.

Розрахунки темпу росту

Темп росту, Тр %
базисний	ланцюговий
-	-
122,0729555	122,073
127,4465581	104,402
130,3000588	102,239
133,9870563	102,830
154,4028241	115,237
154,7362228	100,216
159,7862326	103,264
159,9823495	100,123
168,1898411	105,130
171,7101392	102,093
185,7521083	108,178
186,7228868	100,523
190,0764856	101,796
190,8021181	100,382
194,2733869	101,819
203,9615611	104,987
204,6969994	100,361
229,594038	112,163
232,7711316	101,384

Розраховується:

Тр_баз=Y_i/Y₁*100%;

Тр_ланц=Y_i/Y_i-1*100%.

Таблиця 4.4.

Розрахунки темпу приросту

Темп приросту, ∆Т %
базисний	ланцюговий
-	-
22,07295548	22,073
27,44655815	4,402
30,30005884	2,239
33,98705629	2,830
54,40282408	15,237
54,73622279	0,216
59,78623259	3,264
59,98234948	0,123
68,18984115	5,130
71,71013924	2,093
85,75210826	8,178
86,72288684	0,523
90,07648559	1,796
90,80211806	0,382
94,27338694	1,819
103,9615611	4,987
104,6969994	0,361
129,594038	12,163
132,7711316	1,384

Розраховується:

∆Т_баз=Тр_баз-100%;

∆Т_ланц=Тр_ланц-100%.

Таблиця 4.5.

Розрахунки абсолютного значення 1% приросту

Абсолютне значення 1% приросту, А%
базисний	ланцюговий
-	-
101,98	101,98
101,98	124,49
101,98	129,97
101,98	132,88
101,98	136,64
101,98	157,46
101,98	157,8
101,98	162,95
101,98	163,15
101,98	171,52
101,98	175,11
101,98	189,43
101,98	190,42
101,98	193,84
101,98	194,58
101,98	198,12
101,98	208
101,98	208,75
101,98	234,14

Розраховується:

А_баз=∆Y_баз/∆Т_баз;

А_ланц=∆Y_ланц/∆Т_ланц.

Середній рівень інтервального ряду: Y̅=∑Y/n=17343,05

Середній абсолютного приросту: ∆Y̅=∑∆Y_ланц/n=712,6315789

Середній темпу росту: Tp̅= =1,235185769 або Tp̅= *100%=123,5185769%

Середній темпу приросту: ∆T̅=Tp̅-100%=23,51857693%

Розділ 5

Індексний метод

В аналітичній роботі зі статистичними даними часто оперують різнорідними елементами. Об'єднання різних елементів в одну сукупність називають агрегатом. Для аналізу змін, що відбуваються в таких агрегатах, найкращим прийомом вважається розрахунок індексів.

Статистичні індекси - це відносні величини, які одержують у результаті порівняння складних економічних явищ, утворених з різнорідних елементів, що не підлягають безпосередньому підсумовуванню.

Англійський термін “index numbers” означає «число-показник». Статистична практика широко використовує індекси при вивченні економічних явищ. Знання методології побудови індексів значно розширює аналітичні можливості дослідника, збагачує результативну інформацію досліджень.

За допомогою індексів можна характеризувати зміну як у часі, так і в просторі найрізноманітніших показників. Їх поділяють на дві групи: до першої належать об'ємні (сумарні) показники, які виражаються абсолютними величинами; до другої — показники, розраховані на певну одиницю. Останні умовно можна назвати якісними показниками, і виражаються вони у вигляді середніх величин. Зазначена особливість зумовлює поділ індексів на індекси кількісних та індекси якісних показників.

За допомогою статистичних індексів можна відображувати зміну у часі і просторі як окремих простих показників, так і однойменних показників по складних сукупностях.

Класифікують індекси за ступенем охоплення елементів досліджуваного явища та способом побудови. За ступенем охоплення елементів явища індекси поділяють на індивідуальні й загальні.

Індекси, які відображують співвідношення простих одиничних показників, називають індивідуальними, а індекси, що характеризують зміну певного показника в цілому по будь-якій складній сукупності, — загальними. Останні в свою чергу розглядаються за широтою сукупності. Так, зведені індекси, що охоплюють всю сукупність досліджуваних явищ називають тотальними (або загальними), а індекси, які охоплюють частину (групу) елементів сукупності, — груповими (або субіндексами). За способом побудови загальні індекси поділяють на агрегатні, середні із індивідуальних та середнього рівня.

За допомогою індексного методу вирішуються такі завдання:

1. характеристика загальної зміни складного економічного явища чи окремих його елементів (складових);

2. виділення впливу одного з факторів шляхом елімінування впливу інших;

3. відокремлення впливу зміни структури явища на зміну індексованої величини.

Для побудови статистичного індексу необхідно мати вихідну інформацію, як мінімум, за два періоди. Один з таких періодів називається базисним, другий — поточним. Базисний — це період, з яким порівнюють досліджувані явища, поточний — період, що порівнюється. Якщо досліджуються дані за кілька періодів, то один з них (як правило, початковий) буде базисним, а решта — поточними, або звітними.

Основними об'єктами для побудови індексних комплексів є кількість і ціна. Важливе значення має підписна нумерація. За її допомогою позначається період, до якого належать дані. У теорії індексів показник, зміну якого характеризує індекс, називають індексованою величиною, а пов'язану з нею величину, що використовують як постійну, — елімінованою величиною, або вагою. Використання зазначених двох видів величин вважається особливістю індексного методу аналізу.

Аналіз активної частини основних фондів індексним методом та її вплив на обсяг виробництва

Таблиця 5.1.

Вихідні дані

№ підприємства	Обсяг робіт		Основні фонди		Основні фонди
	базис q0	звіт q1	базис Ф0	у т.ч. Аф	звіт Ф1	у т.ч. Аф1
16	18116	17152	5661	2594	7243	3418
17	22764	23738	6937	3234	7949	3797
18	27243	23414	6991	2502	8208	2588
19	16026	15780	3661	1724	4963	2655
20	15696	16315	5364	2610	5838	2109
21	19171	19458	4993	2719	6467	2915
22	14198	13664	3223	2127	3379	2245
23	18572	19384	5153	2813	6227	2986
24	22779	20800	6407	2885	6307	2785
25	11688	13288	6122	3648	6513	1982
26	22404	20875	6039	2367	7391	2982
27	18944	19042	7516	3593	8187	2819
28	21114	19812	5266	2324	6867	2977
29	16417	17511	5354	2205	6023	2389
30	17469	18943	6319	2459	6522	2608
31	10492	12449	5235	2240	5393	2343
32	12840	12997	5126	1661	6338	1996
33	17498	16295	5221	2441	6361	3071
34	8952	10198	4716	2283	6912	2604
35	14462	15746	5107	2111	6016	2004
Разом	346845	346861	110411	50540	129104	53273

1. Визначається фондовіддача активної частини основних фондів 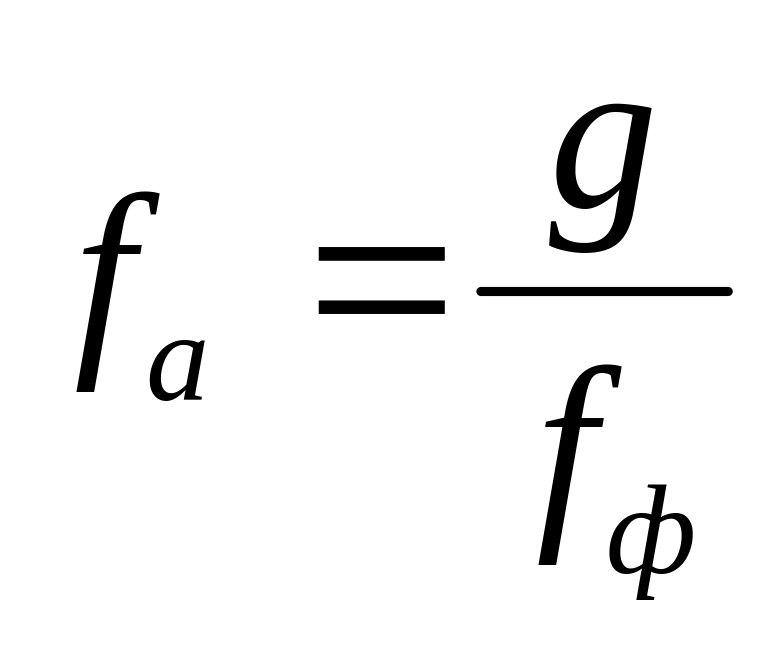, звідси .

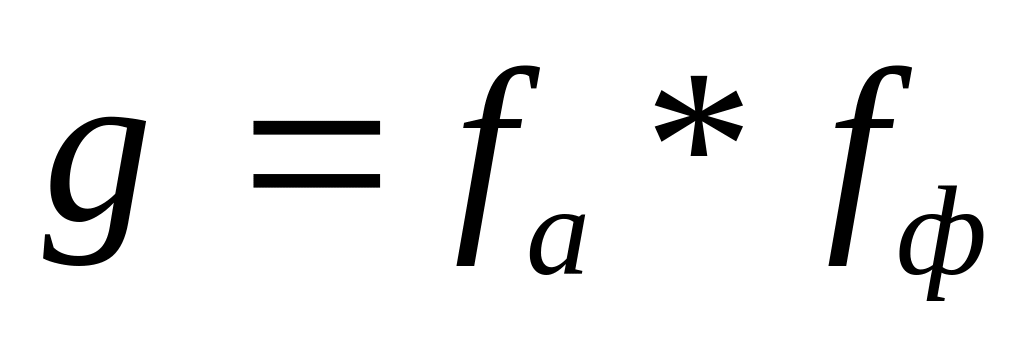2. Установлюється частка активної частини в загальній величині основних фондів , звідси

3. Підставимо значення у формулу , тобто обсяг виробництва представлено як добуток 3-х показників. Визначимо їх вплив.

4. Індексний метод аналізу сукупності підприємств =346861/346845=1,000046.

5. Для визначення впливу окремих факторів на обсяг виробництва використаємо індексну систему

=346861/378540*378540/407320*407320/346845=1,000046.

Вплив f_a , вплив d, вплив Ф

Розрахунки проводимо в таблиці

Таблиця 5.2.