Допоміжні розрахунки для X

XY	X2	Xi-X̅	(Xi-X̅)2
26336816	3928324	-681,65	464646,7225
25942012	3984016	-667,65	445756,5225
31554984	4016016	-659,65	435138,1225
34408335	4447881	-554,65	307636,6225
30675680	5040025	-418,65	175267,8225
29168007	5489649	-320,65	102816,4225
41833779	5707321	-274,65	75432,6225
60595432	6697744	-75,65	5722,9225
26555592	6780816	-59,65	3558,1225
49403344	6801664	-55,65	3096,9225
41895900	7049025	-8,65	74,8225
57928000	7756225	121,35	14725,8225
53679398	7946761	155,35	24133,6225
56720070	8497225	251,35	63176,8225
58980324	8862529	313,35	98188,2225
62249250	8892324	318,35	101346,7225
57880624	8916196	322,35	103909,5225
50041945	9431041	407,35	165934,0225
58625536	11682724	754,35	569043,9225
90133186	14417209	1133,4	1284482,223
944608214	146344715	-	4444088,55

Таблиця 3.3.

Допоміжні розрахунки для y

YX	Y2	Yi-Y̅	(Yi-Y̅)2
17196,649	176570944	-4055,05	16443430,5
17199,656	168922009	-4346,05	18888150,6
17201,374	247936516	-1597,05	2550568,703
17223,925	266179225	-1028,05	1056886,803
17253,135	186704896	-3679,05	13535408,9
17274,183	154977601	-4894,05	23951725,4
17284,062	306635121	167,95	28207,2025
17326,802	548215396	6070,95	36856433,9
17330,239	103999204	-7145,05	51051739,5
17331,098	358837249	1599,95	2559840,003
17341,192	249008400	-1563,05	2443125,303
17369,113	432640000	3456,95	11950503,3
17376,415	362597764	1698,95	2886431,103
17397,033	378613764	2114,95	4473013,503
17410,349	392515344	2468,95	6095714,103
17411,423	435765625	3531,95	12474670,8
17412,282	375739456	2040,95	4165476,903
17430,538	265527025	-1048,05	1098408,803
17505,065	294191104	-191,05	36500,1025
17586,464	563492644	6394,95	40895385,5
346861	6269069287	-	253441621

Щоб визначити тип зв’язку, будуємо кореляційне поле і на ньому ж після рішення системи рівнянь будуємо теоретичну лінію регресії, яка проходить крізь емпіричну.

Рис. 3.1. Графік емпіричної і теоретичної лінії регресії

За емпіричною лінією регресії визначаємо, що графік є лінійним і тому складаємо систему лінійних рівнянь:

= = = =

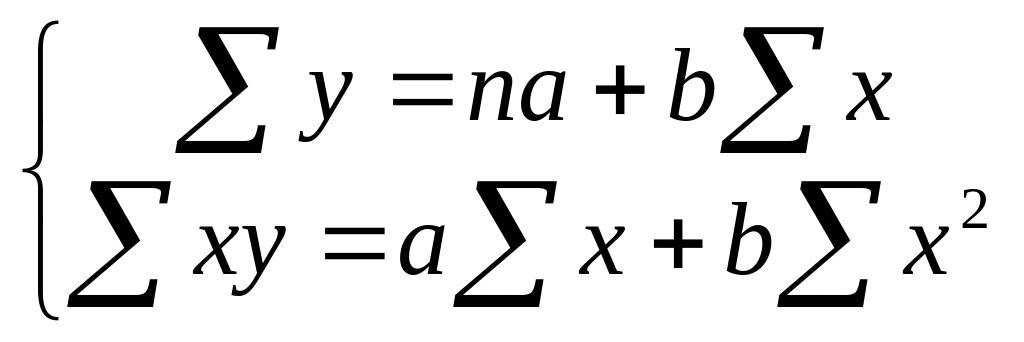Отже, виходить, що y=16770,9666+0,21477422x. З цього випливає, що Y_x буде зазначено в таблиці і поряд з емпіричною лінією регресії на графіку. А також зробимо висновок, що зі зростанням обсягу активної частини основних фондів на 1 тис. грн. збільшується обсяг робіт приблизно на 0,215 тис. грн.

Визначимо тісноту зв’язку за допомогою коефіцієнта кореляції для лінійної залежності:

r=x̅y̅-x̅*y̅/σ_x*σ_y=47230410,7- -2663,65*17343,05/471,39*3559,79=0,61655282

σ_x=

σ_y=

X̅=∑X/n=53273/20=2663,65

Y̅=∑Y/n=346861/20=17343,05

X̅Y̅=∑XY/n=944608214/20=47230410,7

Це означає, що зв'язок суттєвий (середній)..

Зробимо перевірку:

r= =0,61655282

Розділ 4

Аналіз динамічних рядів

Соціально-економічні явища, які вивчаються статистикою, постійно змінюються і розвиваються як у просторі, так і в часі. Одним з важливих завдань статистики є вивчення суспільних явищ в безперервному розвитку і динаміці. Динамікою в статистиці прийнято називати процес розвитку, руху соціально-економічних явищ у часі. Для відображення і аналізу динаміки будують динамічні (хронологічні, часові) ряди. Дослідження динаміки дає змогу охарактеризувати процес розвитку явищ, розкрити основні шляхи, тенденції і темпи цього розвитку.

Рядом динаміки називають ряд статистичних показників, які характеризують зміну суспільних явищ у часі. Кожний ряд динаміки складається з двох обов'язкових елементів: періодів часу (/) і рівнів (у). Показниками часу в рядах динаміки можуть бути або певні дати (моменти) часу, або окремі періоди (роки, квартали, місяці, декади, доба).

Рівнем ряду динаміки називають статистичний показник, який характеризує величину суспільного явища на даний момент або за певний період часу. Вони відображають кількісну оцінку (міру) розвитку досліджуваного суспільного явища.

Рівні динамічного ряду можуть бути виражені абсолютними, відносними і середніми величинами. При аналізі рядів динаміки всі ці величини необхідно використовувати в комплексі, вони мають доповнювати один одного. Рівні ряду динаміки можуть характеризувати величину статистичного показника на певний момент (яку-небудь дату) і за відповідний період часу (рік, місяць, день, годину тощо). В зв'язку з цим розрізняють моментні та інтервальні ряди динаміки.

Моментними називають ряди динаміки, які характеризують розмір явища на певний момент часу. За допомогою моментних рядів динаміки характеризується найчастіше стан умов і факторів виробництва. В моментному ряду динаміки одні й ті самі одиниці сукупності входять до складу кількох рівнів. Тому підсумовування рівнів моментного ряду динаміки не має смислу, так як при цьому підсумки позбавлені економічного змісту. Проте визначення різниці між рівнями моментного динамічного ряду має певний смисл.

Інтервальними називають ряди динаміки, які характеризують розмір явищ за певний період часу. За допомогою інтервальних динамічних рядів як правило характеризуються підсумки виробничого процесу (обсяги виробленої продукції, виконаних робіт, затрат праці, кількості внесених добрив тощо). Рівні інтервального ряду динаміки абсолютних показників на відміну від рівнів моментного ряду не містяться в попередніх або наступних показниках. Тому важливе економічне значення має підсумовування цих рівнів, сума рівнів інтервального ряду динаміки характеризує обсяг досліджуваного явища за більш довгий період. Для виявлення тенденції зміни досліджуваного явища рівні інтервального ряду динаміки можна укрупнювати.

При вивченні динаміки соціально-економічних явищ вирішується цілий ряд завдань, основними з яких є такі:

1. характеристика за допомогою системи показників динаміки інтенсивності зміни рівнів ряду від періода до періода або від дати до дати;

2. визначення середніх значень динамічного ряду за той або інший період;

3. виявлення і кількісна оцінка основної тенденції розвитку (тренда) досліджуваного явища;

4. прогнозування розвитку явища на перспективу;

5. виявлення факторів, що зумовили зміну досліджуваного суспільного явища в часі;

6. аналіз сезонних коливань.

Одним з важливих завдань аналізу рядів динаміки є вивчення особливостей розвитку досліджуваних явищ за окремі періоди. Для виявлення напрямку та інтенсивності змін досліджуваних суспільних явищ за певні періоди часу визначають систему абсолютних і відносних показників динаміки. До таких показників відносяться абсолютний приріст, темп (коефіцієнт) зростання, темп приросту, абсолютне значення одного процента приросту і середні показники ряду динаміки (середній рівень ряду динаміки, середній абсолютний приріст, середній темп зростання і приросту та ін.).

Показники абсолютного приросту, темпу зростання і приросту, а також абсолютного значення одного процента приросту отримують порівнюючи між собою вихідні рівні ряду динаміки. При цьому рівень, з яким порівнюють, називають базисним,а порівнювальний — поточним рівнем.

Для характеристики абсолютної швидкості зростання (зниження) рівнів ряду динаміки обчислюють показник абсолютного приросту (А).

Абсолютний приріст являє собою різницю між двома рівнями, один з яких взято за базу порівняння. Він показує, на скільки одиниць кожен даний рівень відрізняється від рівня, взятого за базу порівняння. Абсолютний приріст може мати додатний або від'ємний знак. Якщо наступний рівень ряду динаміки більший за попередній, то абсолютний приріст буде мати знак «плюс», якщо менше — знак «мінус».

Динамічний ряд абсолютних приростів дає змогу визначити напрям (зростання, зниження) динаміки досліджуваного явища. Крім того, порівнянням абсолютних приростів між собою можна встановити характер зростання або зниження в абсолютному вираженні (рівномірний, прискорений, стрибкоподібний та ін.).

Темп зростання характеризує відносну швидкість зміни явища і показує у скільки разів кожний даний рівень більший або менший рівня, який взято за базу порівняння. Він може бути виражений у вигляді коефіцієнтів або процентів. Темп зростання, виражений у процентах, називають процентом зростання.

Величина темпу зростання буде більшою від одиниці, якщо рівень щодо бази порівняння зростає, і меншою за одиницю, якщо рівень щодо бази порівняння зменшується.

Між ланцюговими і базисними темпами зростання, вираженими коефіцієнтами, є такий взаємозв'язок:

1. добуток ланцюгових коефіцієнтів зростання дорівнює базисному коефіцієнту зростання за відповідний період;

2. частка від ділення двох сусідніх базисних коефіцієнтів зростання дорівнює відповідному ланцюговому коефіцієнту зростання.

Цей взаємозв'язок дає змогу здійснювати перехід від ланцюгових коефіцієнтів зростання до базисних і навпаки.

Поряд з темпами зростання відносна зміна явища у часі може бути також охарактеризована за допомогою темпів приросту які являють собою відношення абсолютного приросту до рівня, взятого за базу порівняння (Т).

Темп приросту, як і абсолютний приріст може бути як додатним, так і від'ємним числом (відповідно при зростанні і зниженні рівня) і виражається у вигляді коефіцієнтів або процентів. На практиці темпи приросту найчастіше виражаються у формі процентів.

Вони показують наскільки процентів збільшився або зменшився поточний рівень порівняно з базисним, взятим за 100%.

Поряд з показниками темпів зростання і приросту в аналізі динамічних рядів викликає інтерес ще один відносний показник, який дає змогу визначити вагомість кожного процента приросту, і те, яка абсолютна величина приховується за цим процентом. Таким показником є абсолютне значення одного процента приросту (П). Він обчислюється як відношення абсолютного приросту до відповідного темпу приросту, вираженого в процентах

Розрахунок цього показника має економічний зміст тільки на ланцюговій основі, оскільки на базисній основі по всіх часових відрізках буде отримано одне і те саме значення показника — сота частина початкового (першого) рівня.

Цей показник має важливе практичне значення в економічному аналізі, оскільки темпи зростання можуть сповільнюватись або залишатися на одному рівні, а абсолютне значення одного процента приросту зростати. Звичайно така закономірність спостерігається в динамічних рядах з рівнями, що постійно зростають.

Слід відмітити, що в динамічних рядах відносних величин (процентів зростання і приросту) їх безпосереднє порівняння можна здійснювати тільки шляхом визначення різниці рівнів. Ці різниці дістали назву пунктів зростання. їх розраховують як різницю базисних процентів зростання або приросту двох суміжних періодів. На відміну від темпів приросту, які не можна підсумовувати та перемножувати, пункти зростання можна підсумовувати, в результаті чого дістанемо темп приросту відповідного періоду порівняно з базисним періодом.

Для отримання узагальнюючих показників динаміки соціально-економічних явищ визначаються різного роду середні величини: середній рівень динамічного ряду, середній абсолютний приріст, середній темп зростання і приросту та ін. Середню з рівнів динамічного ряду називають хронологічною середньою. Середній рівень ряду динаміки характеризує типовий розмір рівнів ряду.

Таблиця 4.1.

Вихідні дані

№ підприємства	Обсяг робіт (валова продукція) Y
34	10198
31	12449
32	12997
25	13288
22	13664
35	15746
19	15780
33	16295
20	16315
16	17152
29	17511
30	18943
27	19042
23	19384
21	19458
28	19812
24	20800
26	20875
18	23414
17	23738
∑	346861

Ряд динаміки можна охарактеризувати такими показниками: абсолютний приріст, темп росту, темп приросту і абсолютне значення 1% приросту.

Таблиця 4.2.