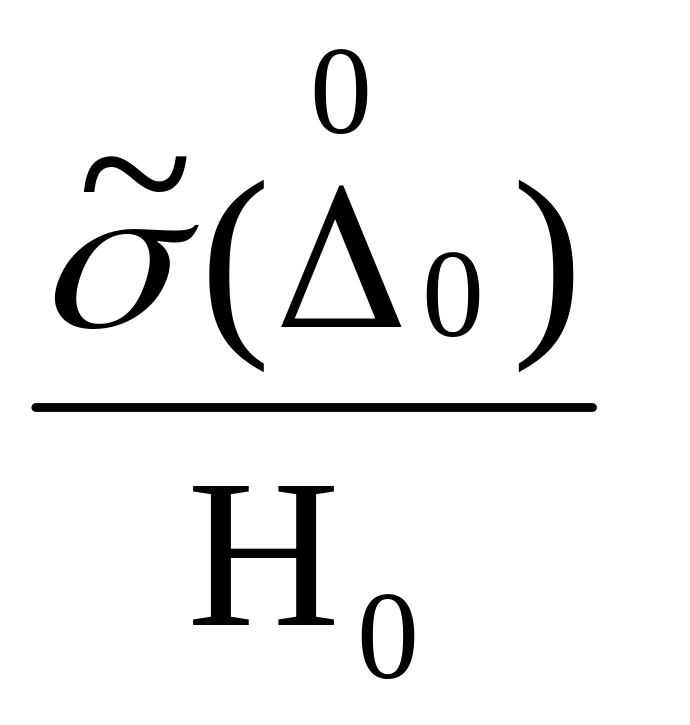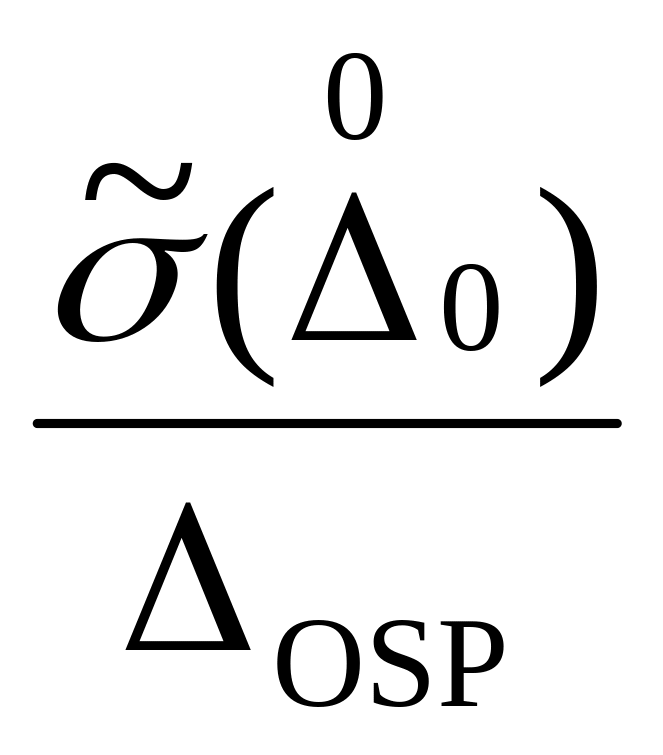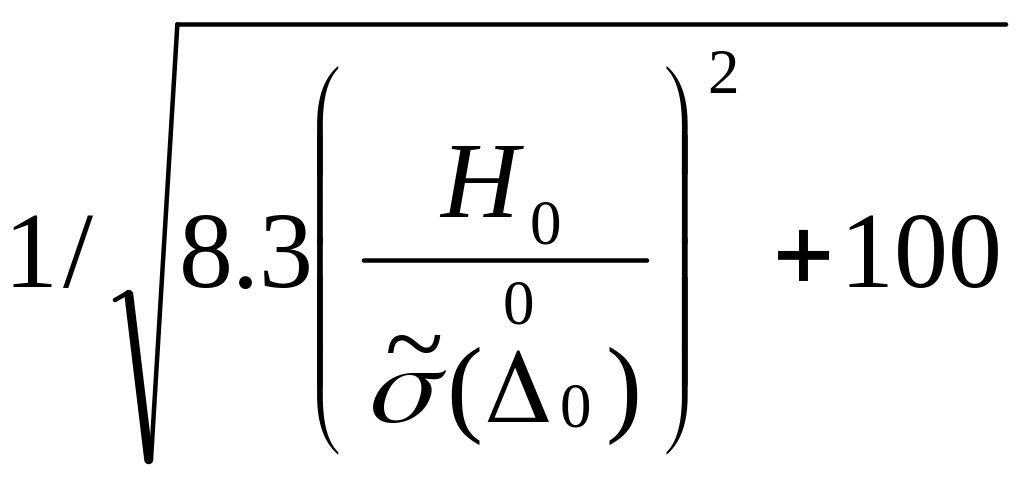28. Нормирование метрологических характеристик средств измерения (мхси ) классами точности

При технических измерениях к каждому средству измерения присваивается определённый класс точности – это обобщённая метрологическая характеристика определяющая различные свойства средства измерения и включает в себя систематическую и случайную составляющую погрешности

Классы точности нормируются пределами допускаемой основной погрешности в виде

1. абсолютной

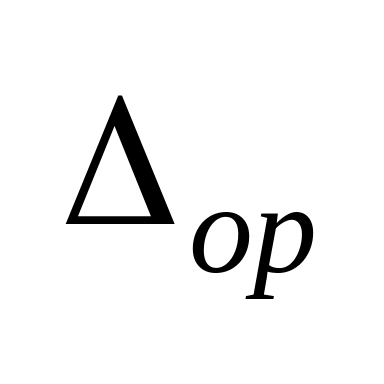
а) для средств измерения, для которых преобладает аддитивная составляющая погрешности ,(1)

б) для СИ и -соизмеримы , (2)

нормируются меры в формулах (1) и (2)

Классы точности указываются на меры, или в виде (3 римская) или «С». Причём чем дальше буква от начала алфавита и чем больше цифра, тем больше погрешность.

29. Нормирование метрологических характеристик по стандарту

В соотв. С ГОСТ-8.009-84 предусматриваются 2 модели нормирования.

1-ая МОДЕЛЬ: включает основную погрешность(ОП), с разделением её на составляющие:

;

где - ОП;

- систематич-я составляющая ОП;

- случайная сост-я ОП;

- случайная сост-я ОП, обусловленная вариацией.

Т.е. в данной модели соизмеримы систематич-е и случ-я сост-ие погр-ти.

Max значение ОП:

, (1)

где - предельное знач-е системат-ой сост-ей ОП. Данная состав-я нормируется всегда, т.к. реальные ср-ва измер-я не могут быть изготовлены идеально точно;

- среднеквадратич. отклонение случ. сост-ей ОП;

Н₀ – вариация ОП.

Если , то она ( ) не нормируется.

Случайные составляющие ОП могут нормироваться обе, или одна из них, если она на 10% > другой. В соотв. с этими правилами составляются 2 нерав-ва, сагласно которым нормируются составляющие ОП.

Таблица нормирования случ. сост-ей ОП ( ). Неравенства:

№	Левая часть	Правая часть
1		≥0.9	<0.1	≥0.1 и <0.9
2		≥0.1	------	≥
		-----	≥0.3	------
нормируется				и

Примечание:

и Н₀ не нормируются, если

1) ,

2) если не выпол-ся 2-е нер-во при выпол-ии 1-го.

2-ая МОДЕЛЬ: применяется для средств измер-ий, у кот. пренебрежимо мала (случ. погр-ть не разделена на составл-ие):

.

Max значение ОП:

, (2)

где - max возможное, для данного типа средств измер-ии, знач-е .

Вариация для 2-ой Мод. признаётся существенной, если выпол-ся нер-во:

.

Дополнит-е динамич-е погр-ти не нормируются в обеих моделях, если выпол-ся усл-е:

1) ;

2) ,

где - max знач-е состав-их дополнит. погр-ти;

- max знач-е динамической погрешности;

- max знач-е погрешности средств измер-и в рабочих усл-ях, включая ОП, дополнит-ю и динамич-ю погрешности.

М/у стандартными традиц-ми харак-ми сущ=ет связь. Зная первые можно найти вторые, но не наоборот.

, (3)

где K=f(p) – функция принятой вероят-ти Р; при р=0.95 k=2.

Составл-ие в (3) зависят от результатов нормирования, состав-их случ. погр-ти и в соотв. с таблицей нормир-я. Например, если нормир-ся обе сост-ие, то определ-ся по (3); если - нормир-ся (одна состав-я), то последнее слагаемое в (3) – отсутсвует. Состав-ие погр-ти формулы(3) называются статистич-ми харак-ми, или приближёнными оценками харак-к погр-ти.