Загальне поняття теорії подібності.

Застосування математичного аналізу до різних типів течії рідини, дає бажаний результат тільки в окремих випадках. Для інших гідродинамічних явищ можливе тільки математичне формулювання задачі, тобто складання диференціальних рівнянь, котрі описують явище, і виявляють умови однозначності, виділяючи одне конкретне явище. Тоді необхідно звертатися до дослідного вивчення окремого випадку гідродинаміки і знаходити зв'язок між характерними для явища величинами у формі емпіричних рівнянь, отриманих на підставі дослідних даних.

Ці рівняння стосуються тільки конкретних випадків, для яких вони отримані, і довільне поширення їх на інші випадки течії рідини, непритаманних досліду, не закономірні. Та це не означає, що одиничні досліди взагалі не можуть бути поширені ні на які інші випадки їх застосування. Це стає можливим тоді, коли результати досліду опрацьовані певним чином. Метод опрацьовування дослідних даних, що робить можливим поширення одного досліду на інші випадки дає вчення про подібні явища. Це вчення дає можливість робити з диференціальних рівнянь і умов однозначності ряд узагальнюючих висновків, не застосовуючи їх інтегрування. На підставі цих висновків можливе таке математичне опрацювання дослідних даних, яке включає в себе всі подібні явища, такі як: геометричну, математичну і матеріальну подібності.

Геометрична подібність.

Геометрично подібні фігури мають такі властивості: відношення їх схожих розмірів є одне і теж число. Якщо розглядати лінійні розміри фігури не тільки як скалярні величини, але й такі, що мають вектор, то подібні фігури мають бути так орієнтовані у просторі, щоб їх схожі сторони були паралельні між собою. Наприклад два подібних паралелепіпеда включають у себе подібні лінії, паралельні між собою. Так ребро АВ|| А^, В^, , а їх відношення - постійне число, яке справедливе для відношення всіх паралельних ліній фігур.

Для отримання чисельного значення цих величин їх потрібно виміряти деяким відрізком ав , вибраним за одиницю довжини. Нехай число l_н показує, скільки разів ав укладається на відрізці прямої АВ. Відповідно l_м є числовим значенням довжини А^,В^,l_н і l_м – так само і для інших елементів подібних фігур.

Таким чином два потоки будуть геометрично подібними, якщо між їх відповідними лінійними розмірами існує постійне співвідношення : (4.1)

де а₁- лінійний масштаб, який показує, у скільки разів розміри моделі l_M менші , порівняно з розмірами натури l_H.

Якби розглядалося відношення інших величин, наприклад, F i F^, площ паралелепіпедів, чи їх об’ємів V i V^, тоді :

для площ F/F^, = (4.2)

для об’ємів V/V^, = (4.3)

Зауважимо, що у геометрично подібних потоках усі розміри, у тому числі і висота шорсткості стінки , повинна бути меншою в моделі, ніж у натури в а₁ разів, і тому шорсткість /R залишається постійною, як і в натурі, тобто /R = idem.

Кінематична подібність.

Рівняння геометричної подібності повинні задовольняти не тільки схожі величини, але й бути справедливими для будь якого сполучення з них, наприклад суми чи різниці, на підставі властивостей пропорції. У кожній парі схожих точок, тобто в точках , повинно мати місце і для співвідношення швидкостей місцевих, максимальних і середніх:

(4.4)

Тобто довільна точка потоку за проміжок часу t_H переміщується на відстань l_H , чи в подібних системах має місце співвідношення: (4.5)

Аналогічно отримуємо співвідношення для прискорень в окремих подібних точках:

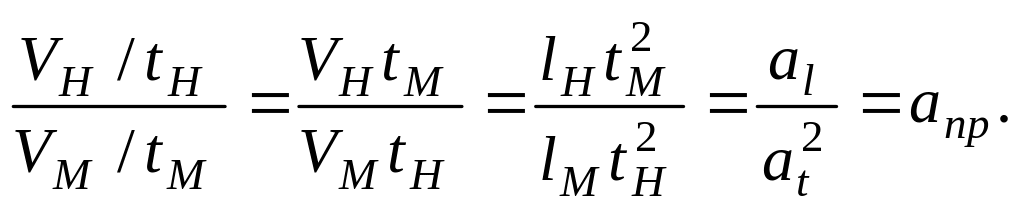
при і .

Тобто кінематична подібність двох систем має місце, якщо відношення швидкостей усіх подібних частинок рідини рівні між собою, а траєкторії руху цих систем геометрично подібні.

Гідродинамічна подібність. Число Ньютона.

Гідродинамічна подібність вимагає динамічної подібності – щоб усі сили, які діють на окремі частинки рідини подібних потоків, відрізнялися між собою лише масштабом при рівних кутах між діючими силами.

Тобто – явища динамічно подібні, коли фізична природа діючих на певну масу рідини сил однакова і вектори цих сил утворюють геометрично подібні силові багатокутники.

У загальному випадку, на довільну частинку рідини діють: - сила тяжіння G, пропорційна густині , прискоренню вільного падіння g , і об’єм V (ч куб лінійного розміру L³):

G = mg = Vg gl³;

- сила Р, викликана гідродинамічним тиском р і пропорційна йому і площі S, (чи квадрату лінійного розміру l²)

P = pS pl²;

- сила тертя, пропорційна в’язкості рідини , швидкості її руху U і лінійному розміру l:

T =

Рівнодіюча цих сил Р_р, згідно з другим законом Ньютона, дорівнює добутку маси на прискорення:

, (4.6)

де а – прискорення потоку рідини. З чисельним значенням сила дорівнює силі інерції | P_p | = | I | .

З умов подібності сил, моделі теж повинні бути подібними:

де а – масштаб всіх сил.

Рівнодіюча всіх сил, згідно з (4.6) запишемо як: Р_р= Va. Тоді рівнодіюча моделі і натури будуть:

В масштабних співмножниках отримаємо:

де і - масштабні множники густини і прискорення.

Враховуючи що - виражений через масштабний співмножник і лінійного розміру то

у такому разі:

(4.7)

або

(4.8)

Залежності (4.7) і (4.8) називаються законом подібності Ньютона в масштабних співмножниках. Якщо ці співмножники виразити у відношенні для натури і моделі їх фактичних значень, отримаємо:

де величина називається числом Ньютона, це міра відношення рушійної сили до сили інерції у потоці.

Запишемо число Ньютона у іншому вигляді, помноживши чисельник і знаменник на l, отримаємо . Через те, що то При цьому закон Ньютона формула (4.7)набуває вигляду:

(4.9)

Основні числа подібності.

Подібність за силою ваги (гравітаційна подібність).Розглянемо рідинну систему масою m , в якій визначальною є сила ваги G :

G = mg,

де G – вага рідини, m – її маса.

Для отримання умов подібності, виконаємо перетворення (4.9) підставивши цей вираз і тоді отримаємо:

Чи (4.10)

Ця безрозмірна величина, яка характеризується відношенням сил інерції і ваги в одному полі називається числом Фруда.

Подібність за силою тиску.

P = pF.

Підставивши значення до рівняння Ньютона отримаємо:

(4.11)

Безрозмірна величина, яка характеризує подібність полів тиску і є мірою відношення сил тиску і інерції у потоці рідини і називається числом Ейлера.

Часто в число Ейлера замість абсолютного тиску вводять значення перепаду тисків р у двох точках потоку, тоді:

(4.12)

Подібність сил тертя.

Підставивши вираз до рівняння подібності отримаємо:

,

звідки виходить, що:

(4.13)

Залежність (4.13) дає дуже малі цифрові значення і тому її змінюють на зворотну і називають числом Рейнольдса. Для круглих труб вводиться як лінійна величина, діаметр d , тоді:

Після заміни динамічної в’язкості на кінематичний коефіцієнт в’язкості отримаємо:

(4.14)

Безрозмірне число подібності Рейнольдса характеризує гідравлічний режим потоку рідини і є мірою відношення у потоці сили інерції до сил молекулярного тертя.

Подібність за силою поверхневого натягу.

Сила поверхневого натягу визначається за формулою: де - коефіцієнт поверхневого натягу, l – одиниця довжини поверхні.

Зробивши відповідні перетворення отримуємо:

(4.15)

Цю величину називають числом Вебера, що є мірою відношення інерційних сил до сил поверхневого натягу.

Число Лагранжа. У деяких випадках числа подібності отримують методом комбінації виведених чисел подібності, так добуток Eu і Re дає число Лагранжа:

(4.16)

Число Лагранжа для течії в’язкої рідини в гладких чи шорстких трубах, характеризує зв'язок безрозмірними полями тиску і швидкості , є мірою відношення сили тиску ( при наявності гідравлічних опорів ) до сили в’язкості.

Характеристика режимів руху за

числами Рейнольдса.

Дослідами Рейнольдса встановлено, що за певних граничних умов, у кожному потоці існує точка переходу від одного режиму руху до іншого. Ця точка визначається критичним числом Рейнольдса Re_кр . Якщо Re < Re_кр, то рух буде ламінарним, коли Re >Re_кр, то потік рідини переходить у турбулентний режим течії. При русі рідини у прямолінійній циліндричній трубі Re_кр = 2320 , але для кожного конкретного випадку руху рідини число Рейнольдса має своє критичне значення.

Для труб не круглого перерізу, відкритих русел, лотків число Рейнольдса визначається через гідравлічний радіус R, тобто Re = vR/v, при цьому Re_кр= 580.

Закономірності рівномірного руху рідини.

Гідравлічні опори.

Розглядаючи рівняння Бернуллі для потоку в’язкої рідини бачимо, що певні труднощі виникають при визначенні втрат напору на подолання гідравлічних опорів. Загальні втрати напору h_w бувають двох типів – по довжині h_l і по місцевих опорах h_i . У загальному випадку, коли мають місце два види опорів, тоді:

,

де - сума втрат напору по довжині, - сума місцевих втрат напору.

Виникнення втрат напору під час руху реальної рідини пов’язані з силами тертя у самій рідині, які характеризуються динамічною в’язкістю:

, (4.17)

де S – площа поверхонь що розглядаються, знак мінус вказує на те, що кожен верхній шар гальмується нижнім, і сила внутрішнього тертя спрямована у протилежний бік руху. Ввівши поняття питомої сили тертя на одиницю поверхні, тоді дотичне напруження становитиме:

Розподіл динамічних напружень при

рівномірному русі.

При рівномірному русі рідини рушійна сила врівноважується силою опору. Для отримання рівняння рівномірного руху у потоці, розглянемо рівномірний рух у трубі на ділянці довжиною l , обмеженій розрізами 1-1, і 11-11.

З механіки відомо, що рівномірний рух можливий тільки за умови, що всі сили врівноважені.

На об’єм рідини, що знаходиться між розрізами діють сили тиску Р₁- зліва, Р₂ –справа, сила тяжіння –G, сила тертя – Т, що чинить опір руху.

Тоді балансове рівняння набуває вигляду:

P₁ – P₂ –G_x – T = 0 . (4.18)

Розглянемо кожен додаток рівняння. Сила гідродинамічного тиску Р₁ збігається з напрямком руху і викликана р₁, тобто Р₁ = р₁F₁. У розрізі 11 – 11, діє сила Р₂ = - р₂ F₂. Тому, що труба має один діаметр F₁ = F₂ = F, тоді ці дві сили проектуються на напрямок руху v. Сила тяжіння в свою чергу діє таким чином: G = g Fl. Проекція сили тяжіння не співпадає з напрямом руху і тому буде від’ємна : - G = G sin

По малюнку видно, що sin і тому:

Остання сила буде силою тертя, що діє на боковій поверхні труби і чинить опір руху рідини. Позначимо питому силу тертя через , а через - змочений периметр живого перерізу F , то повна сила тертя буде:

l.

Знак мінус вказує на те що сила тертя направлена проти руху рідини. Підставивши у вихідне рівняння значення окремих сил, отримуємо:

l. (4.19)

Розділимо всі члени рівняння на :

або

(4.20)

де - гідравлічний радіус

Ліва частина рівняння, це втрачена потенційна енергія. Позначимо всі втрати напору між розрізами 1-1 і 11-11 через h_w отримаємо:

(4.21)

(4.21) – являє собою основне рівняння ізотермічного руху рідини. Поділивши обидві його частини на l і прийнявши до уваги, що h_w/l = i – гідравлічний уклін, отримаємо другий вираз основного рівняння рівномірного руху:

(4.22)

Це рівняння дійсне, для напірного і безнапірного рухів, як для всього потоку, так і для будь якого внутрішнього циліндричного об’єму з радіусом r. Справедливість цього показує умова рівноваги внутрішнього циліндра. Тоді отримаємо:

(4.23)

де - дотичні напруження на бічній поверхні внутрішнього циліндра, R^, - його гідравлічний радіус,

Для кругло – циліндричної труби R = r₀/2 і R= r/2. Поділимо (4.23) на (4.22), матимемо:

звідки

(4.24)

З (4.24) виходить, що при рівномірному русі в круглій трубі дотичні напруження в живому перерізі розподіляються за лінійним радіусом.

Закономірності ламінарного режиму руху.

Розподіл швидкостей у перерізі труби.

Закон Стокса.

Розглянемо ламінарний режим руху рідини у круглій трубі, припустимо, що виконуються такі умови: 1- рух усталений, 2- частинки рідини прилипають до стінок труби ( тобто швидкість на стінці дорівнює нулю). 3 – між шарами, напруження внутрішнього тертя підпорядковане закону Ньютона, який можна записати таким чином:

(425)

Знак мінус ставимо тому, що при збільшенні відстані r градієнт швидкості dU/dr зменшується. Прирівнюючи праві частини рівнянь (4.23), (4.25), матимемо:

,

чи

Розділимо змінні величини:

(4.26)

Запишемо (4.26) у інтегральній формі при :

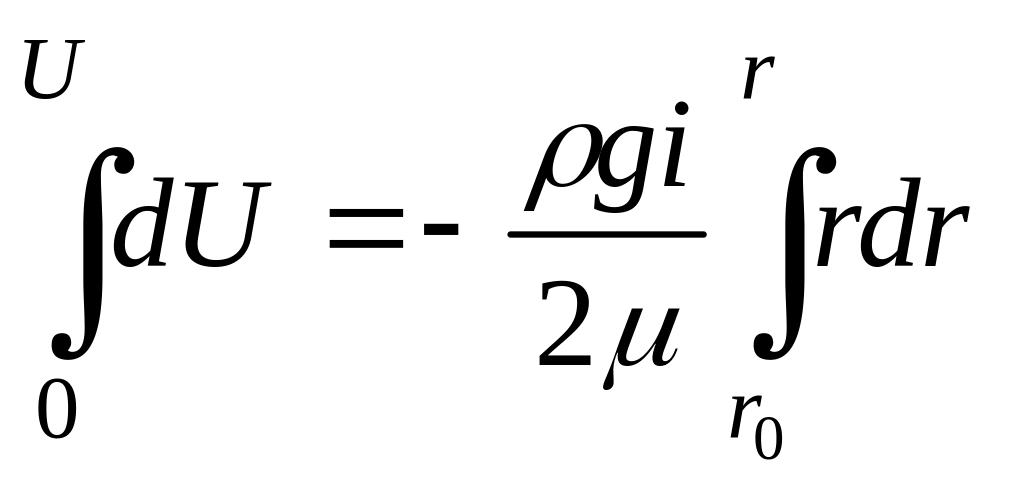
Замінимо межі інтегралу в правій частині і проінтегруємо вираз:

(4.27)

Цю залежність подамо в іншому вигляді. Поділивши чисельник і знаменник на і врахуємо те, що I = h_w/l, і :

(4.28)

Рівняння (4.28) дає можливість визначити швидкість частинки рідини при рівномірному русі у ламінарному потоці. Воно вперше отримане Стоксом у 1867р., є законом розподілу швидкостей у розрізі круглої труби при ламінарному режимі руху.

М аксимальна швидкість на осі труби U_max досягається при r = 0 і визначається з формули:

(4.29)

Мінімальна швидкість на стінці труби при r = r₀, U_max = 0.

Місцеву швидкість U у довільній точці ламінарного потоку визначаємо через U_max з рівнянь (4.27) і (4.29):

(4.30)

Параболічний закон розподілу швидкостей вказує на не рівномірність розподілу швидкостей у живому розрізі потоку.

Визначення витрати рідини і

середньої у перерізі потоку швидкості.

Закон Гагена – Паузейля.

Використовуючи рівняння швидкості частинки рідини у довільній точці розрізу живого потоку, отримаємо формулу для визначення витрати рідини. Розглянемо переріз труби, вісь котрого співпадає з віссю відокремленого розрізу. Внутрішній радіус виділеного кільця r, його ширина у виділеному напрямку dr .

Є площа живого перерізу кільцевого шару рідини з достатньою точністю визначається добутком . Звідки, згідно з законом нерозривності витрати через цю площу будуть:

Підставивши вираз місцевого значення швидкості (4.27) отримаємо:

Про інтегрувавши цей вираз по всьому перерізу труби, дістанемо повні витрати:

або

(4.31)

Ця формула була отримана Гагеном дослідним шляхом у 1839р. і незалежно від нього паризьким фізиком Пуазейлем у 1840р.

Крім цього витрати отримують через середню швидкість потоку рідини, тобто

Через те , що праві частини рівнянь (4.31) і (.432) рівні між собою, то і ліві будуть теж рівні, в наслідок чого :

або

(4.33)

Порівнявши між собою рівняння (4.29) і (4.33) отримаємо вираз:

тобто:

v =0,5U_max. (4.34)

Таким чином, при ламінарному русі рідини в круглій трубі, середня швидкість потоку дорівнює половині максимальної, яка має місце на осі труби.

Коефіцієнт Каріоліса для ламінарного режиму руху рідини.

Коефіцієнт Каріоліса, який входить до рівняння Бернуллі, визначається теоретичним шляхом за формулою: .

Підставимо в це рівняння замість місцевої швидкості U, максимальну U_max з (4.30) і врахуємо, у відповідності з (4.34) v = U_max/2 і dF =2 rdr а F = , отримаємо:

(4.35)

Розкриємо зміст інтеграла:

Підставимо отримане значення інтегралу в (4.35) і переконаємось, що

Така відмінність коефіцієнта Каріоліса від одиниці пояснюється нерівномірністю розподілу швидкостей у живому розрізі, викликана параболічним законом розподілу цих швидкостей.

Втрати напору по довжині трубопроводу.

Використовуючи рівняння (4.33), для середньої швидкості потоку, визначимо втрати напору на одиницю довжини трубопроводу при ламінарному режимі руху рідини:

v

Знаючи, що , отримаємо:

v (4.36).

Ця залежність є ні що інше як формула Пуазейля.

Рівняння Пуазейля показує, що втрати напору при ламінарному режимі руху пропорційність середньої швидкості, залежить від в’язкості рідини, обернено пропорційній квадрату діаметра і не залежить від стану труб.

По всій довжині трубопроводу l втрати напору становлять:

v (4.37).

Врахуємо в рівнянні (4.37) число Рейнольдса, для чого введемо значення vd/Re:

Позначимо через гідравлічний коефіцієнт тертя на одиницю довжини, отримаємо остаточне значення втрат напору по довжині труби( рівняння Дарсі – Вейсбаха ).

( 4.38)

У загальному випадку де А – Коефіцієнт, який залежить від форми живого перерізу.

Початкова ділянка при ламінарному русі рідини.

Параболічний розподіл руху рідини при ламінарному русі, починається не з самого початку труби , а на певній відстані від початку розрізу труби. Якщо рідина потрапляє до труби з плавно заокругленого входу, то швидкість часток біля входу буде однаковою і тільки біля стінок у дуже тонкому шарі, спостерігається майже раптове зменшення швидкості до нуля.

Таке явище пояснюється впливом адгезії ( з латинського – залипання) на межі стінка - рідина. Віддаляючись від вхідного розрізу, струминки в наслідок тертя, зменшують свою швидкість. У центрі потоку швидкість збільшується, тому що у кожному перерізі витрати і швидкість повинні бути однаковими. Цей процес скінчується, коли швидкість у центрі труби досягає свого максимального значення. Таким чином епюра швидкостей змінюється від ( )до параболічної ( )

Теоретично довжина початкової ділянки l_n нескінчена, але для практичних розрахунків приймається за рекомендованим Л. Шиллером рівнянням: . (4.39).

При визначенні втрат напору по довжині труби l, яка перевищує початкову ділянку, тоді втрати напору складаються із втрат на початковій ділянці і на решті довжини труби, тобто:

(4.40)

де Ф – коефіцієнт Френкеля, ( береться із довідників ).

За рекомендацією Френкеля при Ф = 70.

(4.41)

Формули (4.40) і (4.41) стосуються випадку, коли вхід у трубу плавно закруглений. При гострому вході поправка буде більшою за 0,174 і може досягати значення 0,344. На практиці довжину початкової ділянки, при визначенні втрат напору приймають рівною , у залежності від очікуваного числа Рейнольдса.

Закономірності турбулентного руху.

Втрати стійкості руху потоком.

Структура потоку.

Ламінарний рух у трубах переходить у турбулентний не відразу і не по всій трубі. З’являються на окремих ділянках турбулентні місця, які заповнюють не весь переріз труби. Вони можуть збільшуватися і поступово заповнювати весь переріз труби, утворюючи турбулентні пробки, або можуть зменшуватись і зовсім зникати.

Виникнення турбулентних пробок характеризується тим, що на таких ділянках потоку має місце турбулентний режим руху рідини, а поза ним знову ламінарний.

При збільшенні швидкості, турбулентні пробки заповнюють все більші ділянки по довжині труби, доки не зіллються в єдиний турбулентний потік. Якщо швидкість зменшується, тоді весь потік стає ламінарним. Рух, що характеризується місцевими турбулентними збуреннями, коли швидкість не є постійною, називають переміжною турбулентністю, а сам рух перехідним турбулентним рухом. Отже, при великих числах Рейнольдса настає повністю розвинутий турбулентний режим руху рідини.

Одна з найважливіших властивостей турбулентності – не упорядкованість течії. Але турбулентний рух описаний за допомогою теорії імовірності. При цьому визначаються точні – середньостатистичні характеристики руху: швидкість, тиск то що.

Турбулентність можна сформулювати таким чином: - турбулентний рух рідини передбачає наявність неупорядкованої течії, де різні величини зазнають хаотичних змін у часі і просторі, при цьому можуть бути визначені їх середньостатистичні значення.

При турбулентному режимі руху рідини, швидкість біля стінок дорівнює нулю, і миттєво збільшується при підході до центру. При чому, чим ближче до центру тим різкіше зменшується градієнт швидкості dU/dr і при високому ступіні турбулентності стає зовсім малим. Малі градієнти швидкості біля центру викликані високим турбулентним обміном і ведуть до спрямлення лінії розподілу швидкостей порівняно з ламінарним рухом, для якого розподіл швидкостей не рівномірний і відношення середньої швидкості до максимальної становить 0,5.

При турбулентному режимі руху рідини, відношення аналогічних швидкостей буде більшим, так при Re = 2700 = 0,75; Re = 10⁶ = 0,86, Re = 10⁸ = 0,9. Отже, із збільшенням турбулентності відношення . При розподіл швидкостей відповідає випадку руху ідеальної рідини. При цьому біля стінки утворюється тонкий шар котрий прийнято називати в’язким підшар ком. У цьому шарі спостерігаються турбулентні пульсації, які зменшуються завдяки силам внутрішнього тертя . У цьому підшар ку градієнт швидкості найбільший, а характер течії обумовлений в’язким тертям.

Далі йде перехідна зона, де сили в’язкості пропорційні силам інерції. Тобто при турбулентному русі рідини у трубі вплив в’язкості спостерігається у дуже тонкому шарі, який знаходиться біля стінок. Тут швидкість зростає від нуля до майже максимального значення у центрі потоку рідини. Цей шар називається пограничним шаром.

Далі за пограничним шаром знаходиться турбулентне ядро потоку. Де визначальними є опори, котрі можуть, чи повинні, визначатись в’язкістю , турбулентним обміном мас, а напруження відповідає величині:

Біля центру потік рухається майже з однаковою швидкістю, тому градієнт швидкості , тобто сили в’язкості практично відсутні і тому тут переважають сил інерції. Перехід від ламінарного до турбулентного режиму руху настає тоді, коли сили інерції I переважають сили тертя Т, викликані в’язкістю . Тому сили інерції представлені таким чином :

а сили пов’язані з в’язкістю:

Відношення цих сил дає:

Тобто число Рейнольдса на пряму пов’язане з відношенням сил інерції до сил тертя, викликаних в’язкістю рідини.

Товщину в’язкого підшар ку розраховують за імперичною формулою:

,

де - товщина в’язкого підшар ку.

Пульсації швидкості і тиску

при турбулентному режимі руху.

При турбулентному режимі руху дійсна швидкість частинок рідини змінюється не тільки за значенням, але і з напрямком.

Тому середня швидкостей значно спрощує розгляд турбулентної течії. Середню швидкостей можна розрахувати, якщо миттєве значення швидкості U_i Розділити на складові, а саме: - середню місцеву залежну від часу, U^*, та складову пульсації. Для розгляду візьмемо у турбулентному потоці деяку точку, і – з координатами x, y, z. Яка в свою чергу змінює свою швидкість у часі U_i (t) відповідно певній траєкторії.

Врахуємо площу під кривоюU_i(t) скористувавшись інтегралом проміжку часу від Т₀ до Т₀ + Т, і скористаємось теоремою середнього значення:

(4.42)

де - площа прямокутника АВСД, котра в свою чергу рівна площі, що знаходиться під розглядуваною кривою U_i(t) у межах від Т₀ до Т₀ + Т. З виразу (4.42) знайдемо середню швидкість, яка буде висотою прямокутника АВСД.

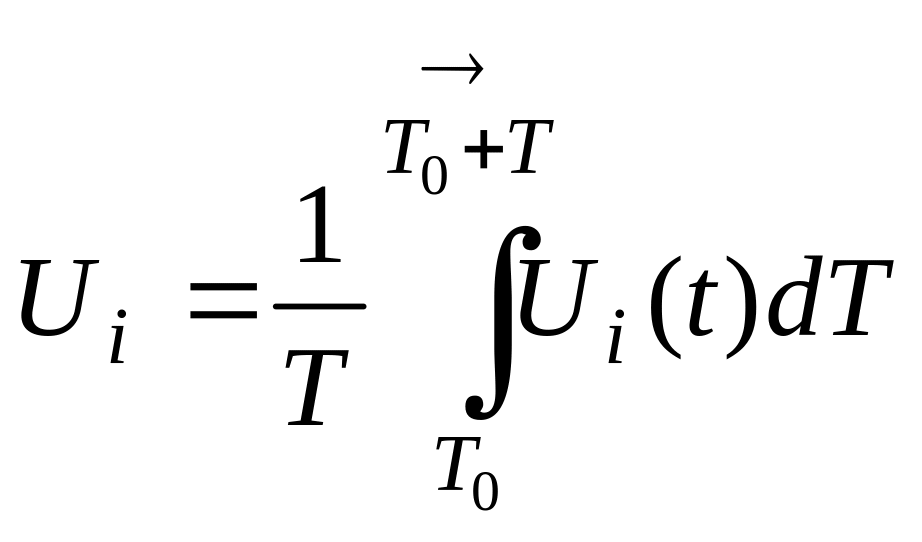(4.43)

У загальному випадку турбулентний рух є не усталеним. Тому введемо поняття місцевої середньої швидкості. У цьому разі, на кордоні де протягом часу умови незмінні (при середній швидкості) рух можна вважати усталеним. І як видно з малюнка місцева швидкість буде:

(4.44)

Тому, для такої моделі стають справедливими всі залежності струминної теорії. Так витрати наприклад розраховують з урахуванням закону розподілу місцевої середньої швидкості по живому перерізу:

,

при цьому середня швидкість складатиме:

.

Розподіл швидкостей у турбулентному потоці.

Довжину перемішування l,під якою розуміють проекцію шляху на вісь Oz, достатнього, щоб частинки потрапляючи з одного шару в інший постійно набували його кінетичних характеристик визначають за залежністю:

(4.46)

де α - стала Кармана, для круглої труби біля 0,4; z – відстань від стінки, у площині живого перерізу, до тієї відмітки де визначається дотичне напруження.

На підставі рівняння ( 4.45) з урахуванням ( 4.46), можна записати:

Приймаючи усталений рух осередненим і плавно змінним, запишемо:

Вираз має розмірність швидкості, яку називають динамічною, чи швидкістю тертя і позначають U_*, тоді маємо:

Розділимо змінні величини і перегрупуємо вираз, тоді

Враховуючи, що U_* і _- сталі після інтегрування отримаємо

Сталу інтегрування С визначаємо з початкових умов. Для труби максимальна осереднена швидкість знаходиться у центрі, тобто при

z = r₀ :

, спростивши вираз отримаємо:

Таким чином, місцеві осередні швидкості в ядрі потоку змінюються за логарифмічним законом.

Тобто. швидкості на стінці труби дорівнюють нулю, в наслідок адгезії між рідиною і стінкою.

На дуже малій відстані від стінок спостерігаються швидкості такої величини, які майже дорівнюють градієнту швидкості у турбулентному ядрі. Тому найбільший градієнт швидкості спостерігають біля стінок.

В області самого ядра швидкості змінюються повільно, звідки градієнт швидкості досягається в наслідок перемішування частинок рідини.

Коефіцієнт Каріоліса при розрахунках у турбулентному потоці приймають за 1.