Основні поняття і терміни гідродинаміки.

Потік рідини – частина безперервного нерозривного руху рідини в обмеженій твердими стінками довільної форми русловій частині.

Вільною поверхнею – називається поверхня потоку, яка знаходиться на межі з навколишнім газовим середовищем.

Безнапірними – називають потоки русла яких мають вільну поверхню.

Напірними – називають потоки русла яки обмежені твердою стінкою і не мають вільної поверхні.

Струменем – називають потік рідини обмежений газоподібною чи рідкою поверхнею.

Живим перерізом потоку – називають поверхню в межах потоку, нормальну у кожній своїй точці до відповідної течії.

Витратою рідини – називається об’єм чи маса рідини яка проходить через живий переріз за одиницю часу.

Швидкість на межі рідина – тверда стінка, дорівнює (0).Величина кожного вектора характеризує місцеву чи локальну швидкість у певній точці Миттєвою швидкістю – називається швидкість визначена у певну мить часу.

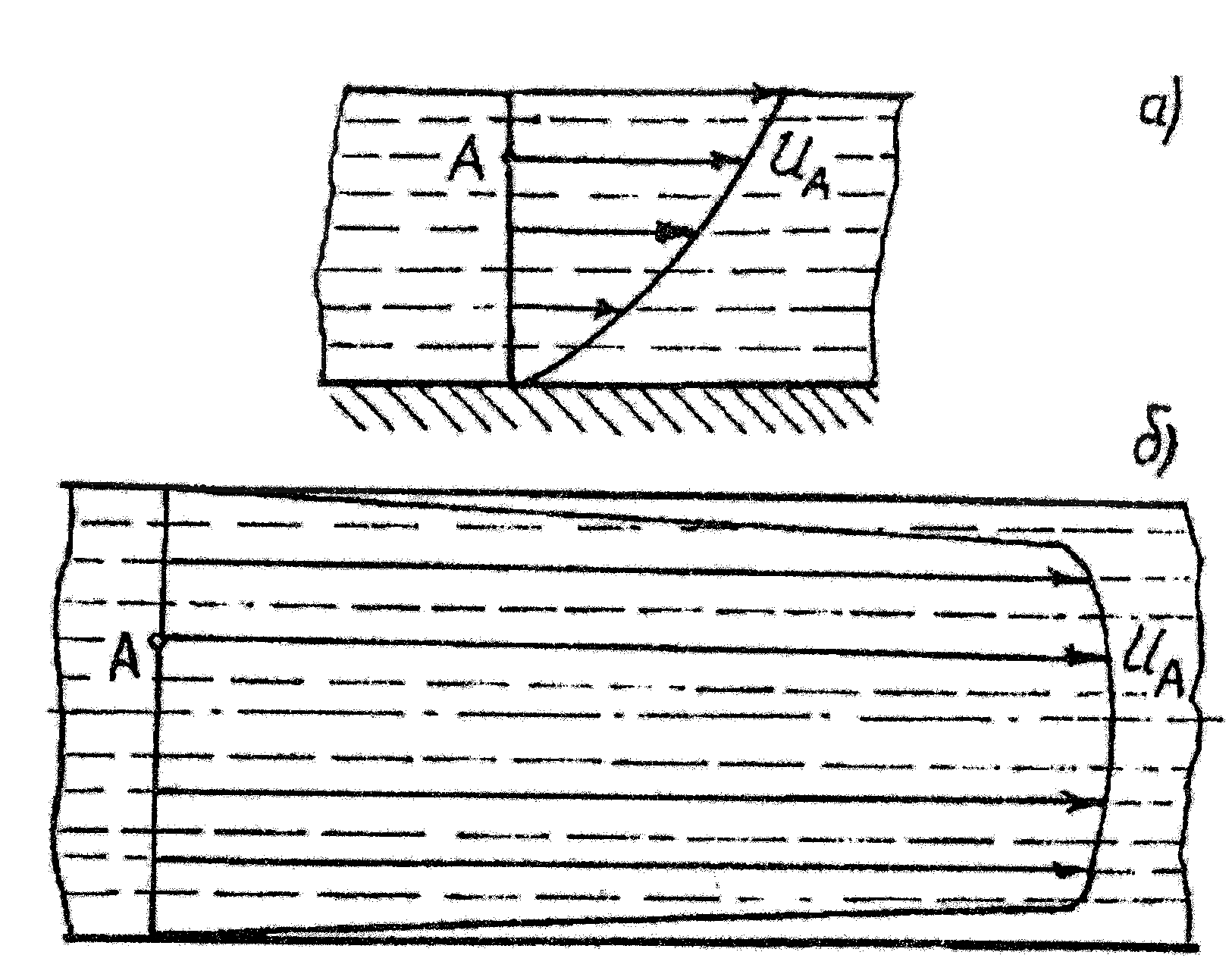
Середня швидкість – це така умовна швидкість, з якою мають рухатися всі частинки рідини через живий переріз, щоб забезпечити таку саму витрату рідини, як і при дійсному розподілі швидкостей. Тобто : V = Q/F або, витрати дорівнюють середній швидкості на площу живого перерізу потоку : Q = VF.

Лінією течії – називається лінія дотична до кожної точки якої у певний момент часу співпадають з напрямом вектора швидкості.

Траєкторія частинки – це шлях, який описує частинка під час руху.

Вивчення лінії течії дає уявлення про кінематику потоку рідини. Розглянемо деяку лінію течії L . Косинуси кута між дотичною і лінією L з осями Ox,Oy,Oz, відповідно дорівнюють : dx/ds; dy/ds; dz/ds, де ds – елемент лінії течії.

Косинуси кутів швидкості V відповідно дорівнюють: Vx/V ; Vy/V ; Vz/V.

За визначення, дотична до лінії течії і вектор швидкості у тій самій точці між собою за напрямком однакові і тоді: dx/ds = Ux/U ; dy/ds =Uy/U ; dz/ds = Uz/U, чи dx/Ux = dy/Uy = dz/Uz = ds/U (3.6)

Диференційне рівняння (3.6) є вихідним для уявлення струминної моделі руху рідини і покладене в основу гідравліки.

На рисунку подана система ліній течії для певного потоку рідини. Будемо вважати рух неусталеним. Тоді карта ліній відповідає миттєвому стану. Виділимо в середині потоку нескінченно малу площу з контуром а,в,с. Поверхня утворена лініями течії, що проходять через контур а,в,с,а, має назву трубка течії, це елементарне русло по якому на протязі дуже малого проміжку часу рухається рідина.

Кількість рідини, що протікає в середині трубки, має назву елементарна струминка.

Для елементарної струминки дійсне співвідношення ; U₁dF₁ = U₂dF₂ чи UdF = const. (3.7)

яке є гідравлічним рівнянням нерозривності, або суцільності течії рідини. Із (3.7) маємо: U₁/U₂ = dF₂/dF₁ , що означає : швидкості в різних живих перерізах елементарної струминки обернено пропорційні площам відповідних перерізів.

Для потоку рідини, котрий складається з нескінченої маси елементарних струминок : v₁F₁ = v₂F₂ (3.8)

що відповідає виразу (3.7), де замість локальної швидкості U, використовується значення середньої v. Це закон нерозривності потоку і відтворює закон збереження маси, виходячи з якого отримаємо : v₁/v₂ = F₂/F₁ (3.9)

Із закону нерозривності потоку (3.8) і рівняння (3.9) виходить, що при усталеному русі рідини із зменшенням площі перерізу середня швидкість збільшується, а при збільшенні - навпаки зменшується, при цьому витрати залишаються однаковими : v₁ F₁ = v₂ F₂ =….. = v_i F_i = Q = idem. (3.10)

У багатьох гідравлічних характеристиках, зустрічається вираз, геометричні розміри. Основним розміром круглої труби, яка працює в напірному режимі, є геометричний радіус (діаметр) труби.

Гідравлічним радіусом живого перерізу називається відношення площі живого перерізу F до змоченого перерізу Х(хі). Під змоченим перерізом розуміємо контур живого перерізу по твердим стінкам русла, лінія перерізу по вільній поверхні не входить до складу змоченого периметру.

R = F/X = r²/2 r = r/2 r.

Для каналу трапецеїдальної форми гідравлічний радіус становитиме : R = (h(B+b)/2) / ((2h/sin a)+b)

Ефективним ( приведеним ) діаметром називається діаметр кола, площа якого дорівнює площі живого перерізу досліджуваного каналу.

Якщо площа перерізу каналу F= d²_пр/4, то ефективний діаметр буде d_пр=

Повний тиск у даній точці є величина : Р = 1/3 (Р_xx + Р_yy + Р_zz )

У випадку коли площина нормальна до вектору швидкості, гідродинамічний тиск буде нормальним до неї, а його величина визначатиметься виразом U²/2.