Интегральное исчисление функции одной переменной Задача 5.
Вычислить неопределенные интегралы. В двух первых примерах а) и б) проверить результаты дифференцированием.
5.1. |
а)
|
б)
|
в)
|
г)
|
5.2. |
а)
|
б)
|
в)
|
г)
|
5.3. |
а)
|
б)
|
в)
|
г)
|
5.4. |
а)
|
б)
|
в)
|
г)
|
|
|
|
|
5.5. |
а)
|
б)
|
в)
|
г)
|
5.6. |
а)
|
б)
|
в)
|
г)
|
|
|
|
|
5.7. |
а)
|
б)
|
в)
|
г)
|
5.8.
а)
б)
в)
г)
5.9.
а)
б)
в)
г)
5.10
а)
б)
в)
г)
Задача 6.
Вычислить определенные интегралы.
6.1. |
а)
|
б)
|
6.2. |
а)
|
б)
|
6.3. |
а)
|
б)
|
6.4. |
а)
|
б)
|
6.5. |
а)
|
б)
|
6.6. |
а)
|
б)
|
6.7. |
а)
|
б)
|
6.8. |
а)
|
б)
|
6.9. |
а)
|
б)
|
6.10. |
а)
|
б)
|
Контрольная работа №2
Раздел 3. Дифференциальные уравнения
Задача 1.
Найти общее решение дифференциального уравнения первого порядка.
1.1.
|
1.2.
|
1.3.
|
1.4.
|
1.5.
|
1.6.
|
1.7.
|
1.8.
|
1.9.
|
1.10.
|
Задача 2.
Найти общее решение дифференциального уравнения второго порядка, допускающие понижение порядка.
2.1.
|
2.2.
|
2.3.
|
2.4.
|
2.5.
|
2.6.
|
2.7.
|
2.8.
|
2.9.
|
2.10.
|
Задача 3.
Найти
частное решение дифференциального
уравнения
,
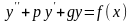удовлетворяющего начальным условиям
,
.
3.1.
|
|
|
3.2.
|
|
|
3.3.
|
|
|
3.4.
|
|
|
3.5.
|
|
|
3.6.
|
|
|
3.7.
|
|
|
3.8.
|
|
|
3.9.
|
|
|
3.10.
|
|
|
