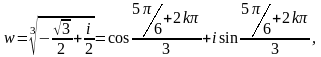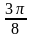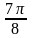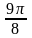1) Длину ребра найдем как длину вектора по формуле [7] 2) Угол между ребрами и найдем как угол между векторами и , пользуясь определением скалярного произведения: [13].

,

; ; .

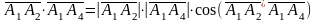2. Площадь грани вычислим с помощью векторного произведения [1]

, ,

3. Объем пирамиды вычислим с помощью смешанного произведения трех векторов, на которых построена пирамида, [9].

4. Уравнение прямой найдем по формуле:

уравнение прямой, проходящей через две точки [1]

.

5. Для того, чтобы составить уравнение плоскости , возьмем текущую точку плоскости. Векторы , , лежат в этой плоскости, т.е. они являются компланарными. Воспользуемся условием компланарности трех векторов:

В силу условия компланарности уравнение плоскости имеет вид:

7) Угол между ребром и гранью (a) найдем по формуле

, где нормальный вектор плоскости , , .

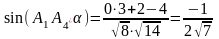8) Чтобы составить уравнение высоты, опущенной из вершины на грань , воспользуемся каноническими уравнениями прямой , где - координаты точки, через которую проходит прямая, а - координаты направляющего вектора [10].

Искомая прямая проходит через точку . Так как прямая и плоскость перпендикулярны, то нормальный вектор плоскости параллелен прямой. Поэтому за направляющий вектор прямой берем вектор . Уравнение прямой, опущенной из вершины , имеют вид : .

Задача 3.

Линия задана уравнением в полярной системе координат. Требуется:

1. построить линию по точкам, начиная от до , придавая значения через промежуток ;

2. найти уравнение данной линии в декартовой системе координат.

Решение.

Для построения линии в полярной системе координат составим таблицу значений полярного радиуса при определенных значениях полярного угла [1]

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
	0
	1,5	1,27	1,1	1,03	1	1,03	1,1	1,27	1,5	1,85	2,33	2,7	3	2,7	2,33	1,85	1,5

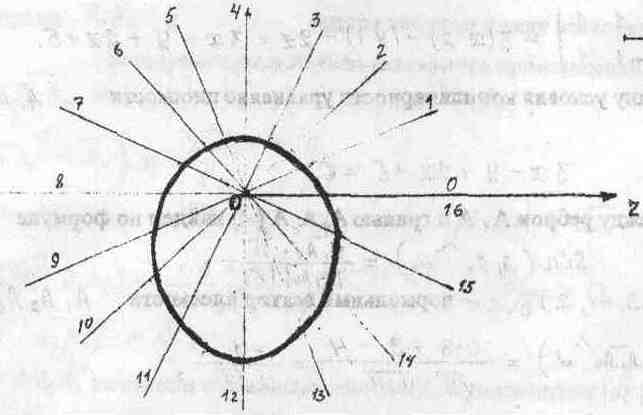
Для получения уравнения в декартовой системе координат используем формулы перехода от полярной системы координат к декартовой:

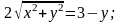
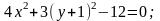
Получили уравнение эллипса с центром в точке (0;-1); большой полуосью b = 2, малой полуосью [1].

Задача 4.

Дана система линейных уравнений

Доказать ее совместность и решить двумя способами:

а) методом Гаусса;

б) матричным методом.

Решение.

Для совместности системы необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы этой системы (теорема Кронекера – Капелли) [1]. Матрица А системы состоит из коэффициентов при неизвестных

Если к матрице системы добавить столбец из свободных членов, то получим расширенную матрицу системы

Под рангом понимается наибольший порядок минора, отличного от нуля. Для матрицы А минором наивысшего порядка, равного трем, является ее определитель [3]:

Следовательно, .

В матрице В нет минора порядка больше 3, а является одним из ее миноров третьего порядка, поэтому .Система совместна, так как .

а) Решение методом Гаусса состоит в преобразовании системы к треугольному виду, что достигается исключением неизвестных х₁ из 2-го и 3-го уравнений и х₂ – из 3-го уравнения. Последовательное исключение неизвестных осуществляется с помощью элементарных преобразований системы, приводящих к равносильной системе, к которым относятся [1]:

1. перестановка любых двух уравнений;

2. умножение обеих частей одного уравнения на любое отличное от нуля число;

3. прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.

Все преобразования, связанные с последовательным исключением неизвестных, удобнее применять не к самой системе линейных уравнений, а к ее расширенной матрице. Получающиеся при этом матрицы называются эквивалентными и соединяются знаком

(вертикальной чертой отделены элементы матрицы А).

Были проведены следующие действия:

1. из элементов второй строчки вычли элементы первой строки;

2. первую и вторую строки поменяли местами;

3. к элементам второй строки прибавили соответствующие элементы первой строки, умноженные на (-2);

4. к элементам третьей строки прибавили соответствующие элемент второй строки.

Полученной матрице соответствует система уравнений:

Решая уравнения снизу вверх, имеем

Ответ: (-1, 2, 2).

б) Для решения системы матричным методом вводим матрицы

Тогда эта система запишется в виде матричного уравнения АХ=С [13].

Умножив левую и правую части уравнения на А^-1 слева, получим

А^-1АХ=А^-1С,где А^-1 – обратная матрица.

Так как А^-1А=Е, то Х=А^-1С.

где

- алгебраическое дополнение, соответствующее элементу ;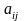

- минор (определитель), который получается из матрицы А после вычеркивания i-ой строки и j-го столбца.

Найдем алгебраические дополнения:

Cледовательно:

Пользуясь правилом умножения матриц получим решение системы [10]:

откуда

Сравните ответы, полученные при решении системы методом Гаусса и матричным методом.

Задача 5.

Дано комплексное число .

Требуется: 1) записать число Z в алгебраической и тригонометрической формах; 2) найти все корни уравнения

Решение.

1) Комплексными называются числа вида z=x+iy, где x и y – действительные числа, а - мнимая единица. Числа x и y называются соответственно действительной и мнимой частями комплексного числа Z. Число z=x-iyназывается сопряженным числу z=x+iy. С геометрической точки зрения числу Z можно сопоставить вектор, направленный из начала координат в точку Z с координатами x и y [7]. Длина этого вектора называется модулем комплексного числа и определяется равенством

.

Угол, образованный вектором Z с положительным направлением оси ОХ, называется аргументом числа Z и обозначается Argz. Для аргумента j справедливы формулы [7]:

значения Argz определяются не однозначно, а с точностью до слагаемого 2kp (k=0; ±1; ±2; …). Argz=аrgz+2kp , где аrgz– главное значение аргумента,

.

Тригонометрическая форма комплексного числа z=x+iyимеет вид [7]

где

- модуль комплексного числа,

- главное значение его аргумента.

Данное число запишем в алгебраической форме. Для этого в числителе раскроем скобки и умножим числитель и знаменатель на число сопряженное знаменателю. Получим:

Чтобы число записать в тригонометрической форме, найдем его модуль и главное значение аргумента:

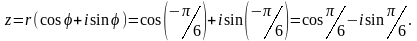
2) Решим уравнение

Чтобы найти все корни n-ой степени из числа Z, воспользуемся формулой [9]:

Для числа найдем модуль и аргумент.

т.к. то

Итак: