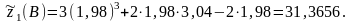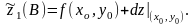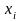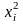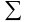Решение типового варианта раздела 2.

Задача 1.

1. дана функция 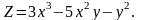Найти частные производные первого и второго порядка. Доказать, что смешанные производные равны.

Решение.

(производная по х найдена в предположении, что у – постоянная величина в момент дифференцирования).

(производная по у найдена в предположении, что х – величина постоянная в момент дифференцирования) [10].

1.2. Проверить, что функция удовлетворяет уравнению

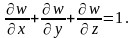
Решение.

Находим (y , z – постоянные).

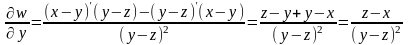
(x, z – постоянные).

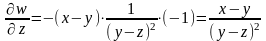(x, y – постоянные).

Подставим найденные производные в данное уравнение:

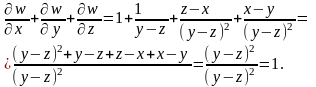
Задача 2.

Дана функция и две точкиА(2; 3) и в(1,98; 3,04).

Требуется:

1. вычислить значение в точкеВ; 2) вычислить приближенное значение функции в точке В, исходя из значения функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости и нормали к поверхности в точке С(2; 3; ).

Решение.

так как

1. 

2. 

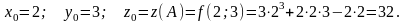
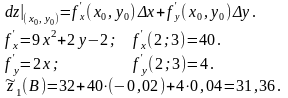
3) относительная погрешность вычисляется по формуле

4) запишем уравнения касательной плоскости и нормали к поверхности в точке соответственно [13]:

Для нашей задачи эти уравнения примут вид:

или 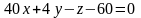- уравнение касательной плоскости;

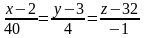- уравнение нормали к заданной поверхности в точке (2, 3, 32).

Задача 3.

Исследовать на экстремум функцию

Решение задачи состоит из трех частей.

1. С помощью необходимого условия существования экстремума, то есть из системы

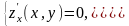найдем координаты стационарных (критических) точек [10].

2. Проверим выполнение достаточного условия существования экстремума в каждой из стационарных точек. Для этого составим где

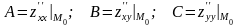
и вычислим значение в каждой стационарной точке. Те стационарные точки, в которых значение 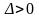, будут являться точками экстремума.

3. Решим вопрос о характере экстремума. Точка 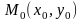будет точкой максимума, ес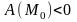ли , и точкой минимума, если

Решение.

Для заданной функции и 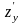всегда существуют и для нахождения стационарных точек запишем систему уравнеий:

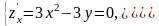или

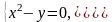
Решение системы: Получаем две стационарные точки 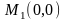и .

Найдем:

Составим

Вычислим в точке 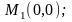то есть 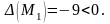Делаем вывод, что в точке экстремума нет. Значение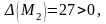 следовательно в точке экстремум есть, причем точка является точкой минимума, так как

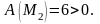
Задача 4.

Экспериментально получены значения искомой функции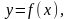 которые записаны в таблицу. Методом наименьших квадратов найти функцию в виде

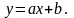
	15	18	21	24	27	30	33	36	39	42
	4,5	5,2	5,8	6,3	7,0	7,7	8,3	8,8	9,5	10

Решение.

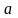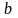Если по данным таблицы построить точки, то по чертежу увидим, что точки располагаются вдоль прямой. Поэтому аппроксимирующую функцию будем искать в виде Для определения коэффициентов и в соответствии с методом наименьших квадратов составляем систему уравнений:

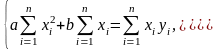
Для удобства вычислений сумм составим таблицу.

1	15	4,5	225	67,5
2	18	5,2	324	93,6
3	21	5,8	441	121,8
4	24	6,3	576	151,2
5	27	7,0	729	189,0
6	30	7,7	900	231,0
7	33	8,3	1089	273,9
8	36	8,8	1296	316,8
9	39	9,5	1521	370,5
10	42	10,0	1764	420,0
	285	73,1	8865	2235,3

Составим систему уравнений:

Для решения системы умножим первое уравнение на (-10), второе – на 285. Сложив их, получим отсюда

Тогда

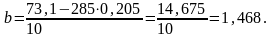
Следовательно, искомая аппроксимирующая функция имеет вид:

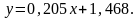
Замечание.

Систему уравнений можно решать любым способом.

Задача 5.

Найти неопределенные интегралы. В примерах 5.1 (а,б),5.2 (а) результаты интегрирования проверить дифференцированием.

5.1.(а)

Решение.

Преобразуем подынтегральную функцию так, чтобы в числителе получилась производная знаменателя:

Проверка:

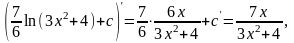
То есть производная от первообразной функции равна подынтегральной функции [7].

5.1. (б)

Решение.

Данный интеграл можно привести к табличному, если подвести часть подынтегральной функции под знак дифференциала и ввести компенсирующий множитель.

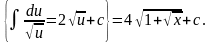
Проверка:

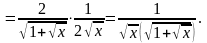
5.1. (в)

Решение.

Используется формула 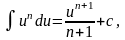где

.

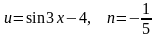5.1. (г)

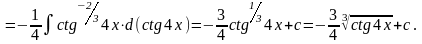
так как где .

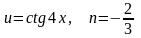5.1.(д)

Решение.

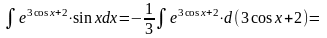
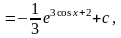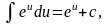так как где

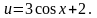
5.2.(а)

Решение.

Интеграл вида 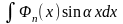берется по частям, так как подынтегральная функция представляет собой произведение алгебраической функции на трансцендентную, то есть по формуле:

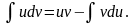
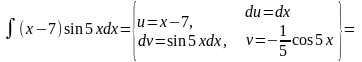
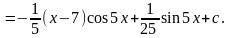
Проверка:

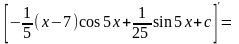
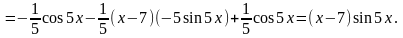
(для проверки была использована формула .

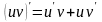5.2.(б)

Решение.

Интеграл от обратных тригонометрических функций берется по частям.

(последний интеграл берется с помощью формулы ).

5.2(в)

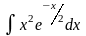
Интеграл вида 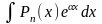берется по частям, так как подынтегральная функция представляет произведение алгебраической функции на трансцедентную.

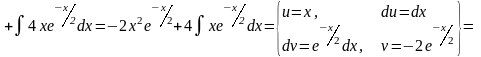
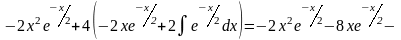
В данном примере формула интегрирования по частям была использована дважды.

5.3. (а)

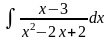
Решение.

Данный интеграл является интегралом от простейшей рациональной дроби третьего типа (квадратный трехчлен имеет отрицательный дискриминант) [7]. При интегрировании в числителе запишем производную от квадратного трехчлена и выравниваем коэффициенты по условию. После почленного деления и выделения полного квадрата в знаменателе получаем

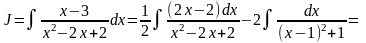
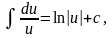(Первый интеграл берется по формуле: где . Второй интеграл берется по формуле:

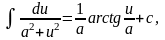где ).

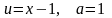5.3. (б)

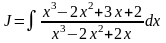
Решение.

Подынтегральная функция представляет собой неправильную рациональную дробь.

Выделим целую часть [4]:

Полученную правильную рациональную дробь разложим на простейшие дроби, предварительно разложив знаменатель на простые множители:

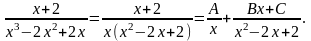
Справа приводим дроби к общему знаменателю и записываем равенство числителей:

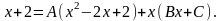
Коэффициенты А, В, С, находим методом частных значений, подставляя в полученное равенство вместо Х вещественные корни знаменателя:

Для определения остальных коэффициентов берем дополнительные значения Х:

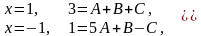
Найденные значения А, В, С подставляем в разложение дроби и получаем интеграл

(см. предыдущий пример)

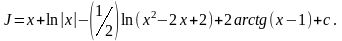
5.3. (в)

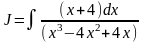
Интегрируем правильную рациональную дробь, разлагая ее на простейшие дроби:

Справа приводим дроби к общему знаменателю и записываем равенство числителей:

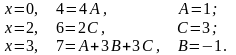
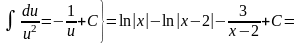
5.3. (г)

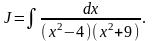
Решение.

Для интегрирования данной правильной рациональной дроби нужно разложить ее на простейшие дроби, а затем, как в предыдущем примере, найти коэффициенты и проинтегрировать каждую из простейших дробей. Однако этот интеграл можно взять иначе, учитывая, что в знаменателе стоят скобки, и выполняя преобразование числителя:

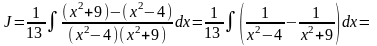
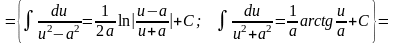
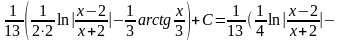
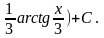
5.4. (а)

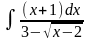
Решение.

Подынтегральная функция содержит иррациональное выражение. Для интегрирования таких выражений делается замена, устраняющая иррациональность.

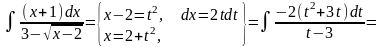
Замечание.

После замены переменной под знаком интеграла дробь стала неправильной, поэтому сначала пришлось выделить целую часть, а затем проинтегрировать полученное выражение.

5.4.(б)

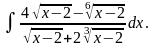
Решение.

Иррациональное выражение под знаком интеграла содержит корни с разными показателями. Поэтому делается замена переменной: где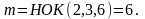

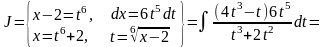
(Выделим целую часть)

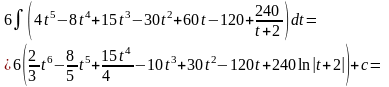
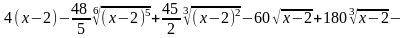
5.4. (в)

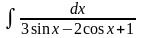
Решение.

Для интегрирования тригонометрического выражения, стоящего под знаком данного интеграла, используется универсальная тригонометрическая подстановка, которая сводит указанный интеграл к интегралу от рациональной дроби.

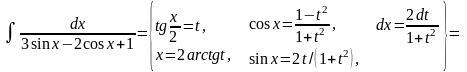
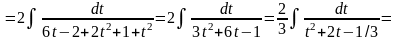
(В знаменателе выделим полный квадрат)

(При интегрировании использовали формулу: ).

5.4. (г)

Решение.

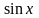Для интегрирования тригонометрической функции, четной относительно и , делается замена 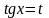, которая сводит данный интеграл к интегралу от рациональной дроби.

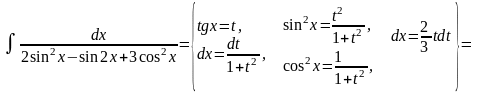
(В знаменателе выделим полный квадрат)

При интегрировании использовали формулу:

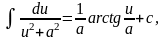
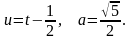
Задача 6.

Вычислить определенный интеграл

6(а).

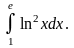
Решение.

Используем формулу интегрирования по частям для определенного интеграла:

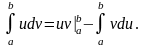
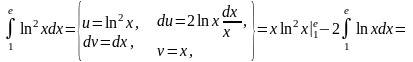
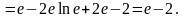
(При решении данного примера формула интегрирования по частям была использована дважды).

6(б).

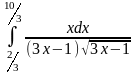
Решение.

Данный интеграл приводится к интегралу от рациональной функции с помощью подстановки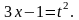 С помощью этой же подстановки пересчитаваются пределы интеграла [4]:

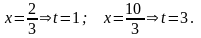
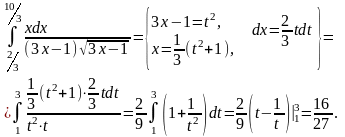
Замечание. При интегрировании рациональной дроби выполнено почленное деление числителя на знаменатель.