§ 1.4. Частота события. Статистическое определение вероятности

Классическое определение вероятности предполагает, что все элементарные исходы равновозможны. О равновозможности исходов опыта заключают в силу соображений симметрии (как в случае монеты или игрального кубика). Задачи, в которых можно исходить из соображений симметрии, на практике встречаются редко. Во многих случаях трудно указать основания, позволяющие считать, что все элементарных исходы равновозможны. В связи с этим появилась необходимость введения еще одного определения вероятности, называемого статистическим. Чтобы дать это определение, предварительно вводят понятие относительной частоты события.

Относительной частотой события, или частотой, называется отношение числа опытов, в которых появилось это событие, к числу всех произведенных опытов. Обозначим частоту события А через W(A), тогда по определению

W(A)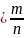 , (1.4.1)

где m – число опытов, в которых появилось событие А; n – число всех произведенных опытов.

Частота события обладает следующими свойствами.

1. Частота случайного события есть число, заключенное между нулем и единицей:

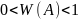. (1.4.2)

2. Частота достоверного события U равна единице:

W(U)=1

3. Частота невозможного события V равна нулю:

W(V)=0

4. Частота суммы двух несовместимых событий A и B равна сумме частот этих событий:

W(A+B)=W(A)+W(B)

Наблюдения позволили установить, что относительная частота обладает свойствами статистической устойчивости: в различных сериях многочленных испытаний (в каждом из которых может появиться или не появиться это событие) она принимает значения, достаточно близкие к некоторой постоянной. Эту постоянную, являющуюся объективной числовой характеристикой явления, считают вероятностью данного события.

Вероятностью события называется число, около которого группируются значения частоты данного события в различных сериях большого числа испытаний.

Это определение вероятности называется статистическим.

В случае статистического определения вероятность обладает следующими свойствами: 1) вероятность достоверного события равна единице; 2) вероятность невозможного события равна нулю; 3) вероятность случайного события заключена между нулем и единицей; 4) вероятность суммы двух несовместимых событий равна сумме вероятности этих событий.

П р и м е р 1 . Из 500 взятых наудачу деталей оказалось 8 бракованных. Найдите частоту бракованных деталей.

Р е ш е н и е . Так как в данном случае m=8, n=500, то в соответствии с формулой (1.4.1) находим

.

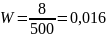П р и м е р 2 . Игральный кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова частота появления шестерки?

Р е ш е н и е . Из условия задачи следует, что n=60, m= 10, поэтому

.

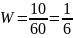П р и м е р 3 . Среди 1000 новорожденных оказалось 515 мальчиков. Чему равна частота рождения мальчиков?

Р е ш е н и е . Поскольку в данном случае n=1000, m=515, то

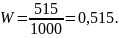
П р и м е р 4 . В результате 20 выстрелов по мишени получено 15 попаданий. Какова частота попаданий?

Р е ш е н и е . Так как n=20, m=15, то

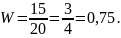
П р и м е р 5 . При стрельбе по мишени частота попаданий W=0,75. Найдите число попаданий при 40 выстрелах.

Р е ш е н и е . Из формулы (1.4.1), следует что m=Wn. Так как W=0,75, n=40, то m=0,75·40=30. Таким образом, было получено 30 попаданий.

П р и м е р 6 . Частота нормального всхода семян W=0,97. Из высеянных семян взошло 970. Сколько семян было высеяно?

Р е ш е н и е . Из формулы (1.4.1) следует, что 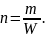Поскольку m=970, W=0,97, то n=970/0,97=1000. Итак, было высеяно 1000 семян.

П р и м е р 7 . На отрезке натурального ряда от 1 до 20 найти частоту простых чисел.

Р е ш е н и е . На указанном отрезке натурального ряда чисел находятся следующие простые числа: 2, 3, 5, 7, 11, 13, 17, 19; всего их 8. Так как n=20, m=8, то искомая частота

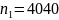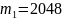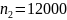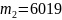П р и м е р 8 . Проведены 3 серии многократных подбрасываний симметричной монеты, подсчитаны числа появления герба: 1) , ; 2) , ; 3) 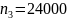, 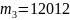. Найти частоту появления герба в каждой серии испытаний.

Р е ш е н и е . В соответствии с формулой (1.4.1) находим:

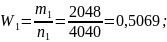
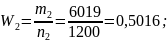
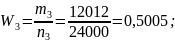
З а м е ч а н и е. Эти примеры свидетельствуют о том, что при многократных испытаниях частота события незначительно отличается от его вероятности. (Вероятность появления герба при подбрасывании монеты p=1/2=0,5 , так как в этом случае n=2, m=1).

П р и м е р 9 . Среди 300 деталей, изготовленных на автоматическом станке, оказалось 15, не отвечающий стандарту. Найдите частоту появления нестандартных деталей.

Р е ш е н и е . В данном случае n = 300, m = 15, поэтому

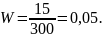
П р и м е р 10 . Контролер, проверяя качество 400 изделий установил, что 20 из них относятся ко второму сорту, а остальные – к первому. Найдите частоту изделий первого сорта, частоту изделий второго сорта.

Р е ш е н и е . Прежде всего, найдем число изделий первого сорта: 400 – 20 = 380 . Поскольку n = 400, 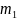= 380 , то частота изделий первого сорта

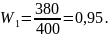
Аналогично находим частоту изделий второго сорта:

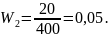
Задачи

1. Отдел технического контроля обнаружил 10 нестандартных изделий в партии из 1000 изделий. Найдите частоту изготовления бракованных изделий.

2. Для выяснения качества семян было отобрано и высеяно в лабораторных условиях 100 штук. 95 семян дали нормальный всход. Какова частота нормального всхода семян?

3. Найдите частоту появления простых чисел в следующих отрезках натурального ряда: а) от 21 до 40; б) от 41 до 50; в) от 51 до 70.

4. Найдите частоту появления цифры при 100 подбрасываниях симметричной монеты. (Опыт проводите самостоятельно)

5. Найдите частоту появления шестерки при 90 подбрасываниях игрального кубика.

6. Путем опроса всех студентов Вашего курса определите частоту дней рождения, попадающих на каждый месяц года.

7. Найдите частоту пятибуквенных слов в любом газетном тексте.

Ответы

1. 0,01. 2. 0,95; 0,05. 3. а) 0,2; б) 0,3; в) 0,2.

Вопросы

1. Что такое частота события?

2. Чему равна частота достоверного события?

3. Чему равна частота невозможного события?

4. В каких пределах заключена частота случайного события?

5. Чему равна частота суммы двух несовместимых событий?

6. Какое определение вероятности называют статистическим?

7. Какими свойствами обладает статистическая вероятность?