§ 1.3. Комбинаторика и вероятность

Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используют при непосредственном вычислении вероятностей. Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только спс порядком, называются перестановками этик элементов. Число всевозможных перестановок из n элементов обозначают через Рn; это число равно n! (читается эн-факториал):

Pn=n!, (1.3.1)

где

Pn! = 1*2*3*... n, (1.3.2.)

З а м е ч а н и е 1. Для пустого множества принимается соглашение: пустое множество можно упорядочить только одним способом; по определению полагaют 0! = 1.

Размещениями называют множества, составленные из n различных элементов по т элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений определяется формулой

An^m = n(n-1)(n-2)…(n-m+1). (1.3.3)

Сочетаниями из n различных элементов по m называются множества, содержащие m элементов из числа n заданных, и которые отличаются хотя бы одним элементом. Число сочетаний из n элементов по т обозначают: Сn^m или (_n^m ). Это число выражается формулой

C_n^m = 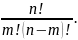(1.3.4)

З а м е ч а н и е 2. По определению полагают C„° =1.

Для числа сочетаний спpаведливы равенства:

Cn^m = C_n^n-m, C_n+1^m+1 = C _n ^m + C_n^m+1, (1.3.5)

С„°+С_n¹ + C_n ² + … + C_n^n-1 + C_nⁿ = 2ⁿ. (1.3.6)

Последнее равенство иногда формулируется в виде следующей теоремы o конечных множествах.

Число всех подмножеств множества, состоящего из из n элементов, равно 2".

Отметим, что числа перестановок, размещений и сочетаний связаны равенством

Cn^m =

З а м е ч а н и е 3. Выше предполагалось, что все n элементы различны. Если же некоторые элементы повторяются, то в этом случае множества c повторниями вычисляют по другим формулам.

Например, если среди n элементов есть n1 элементов одного вила, n2 элементов другого вида и т.д., то число gерестановок c повторениями определяется формулой

Pn(n1,n2,…,nn)= (1.3.7)

где n1+n2+...+nk =n.

Число размещений по m элементов c повторениями из п элементов равно n^m , т. e.

(An^m)c повт = n^m (1.3.8)

Число сочетаний c повторениями из n элементов по m элементов равно числу сочетаний без повторений из n+m — 1 элементов по m элементов, т.e.

(Сn ^m )_{c повт} = Cn+m-1 ^m. (1.3.9)

При решении задач комбинаторики используют следующие правила.

Правило суммы. Если некоторый объект A может быть выбран из множества объектов m способами, a другой объект B может быть выбран n способами, то выбрать либо A, либо B можно m + n способами.

Правило произведения. Если объект A можно выбрать из множества объектов т способами и после каждого такого выбора объект В можно вы брать n способами, то пара объектов (А, B) в указанном порядке может быть выбрана m * n способами.

Классическая схема подсчета вероятностей пригодна для решении ряда сугубо практических задач. Рассмотрим, например, некоторое множество элементов объема N. Это могут быть изделия, каждое из которых является годным или бракованным, или семена, каждое из которых может быть всхожим или нет. Подобного рода ситуации опи-

сываются урновой схемой: в урне иместся N шаров, из них M голубых, (N-M) красных.

Из урны, содержащей N шаров, в которой находится ,M голубых шаров, извлекается n шаров. Требуется определить вероятность того, что в выборке объема n будет обнаружено m голубых шаров. Обозначим через А событие "в выборке объема n имеется т голубых шаров", тогда

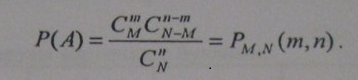
П р и м е р 1. Сколькими различными способами можно выбрать три лица на три рaзличные должности из десяти кандидатов?

Р е ш е н и е. Воспользуемся формулой (1.3.3). При n= 10, m= 3 получаем

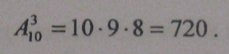
П р и м е р 2. Сколькими различными способами могут разместиться на скамейке 5 человек?

Р е ш е н и е. Согласно формуле (1.3.1) при n=5 находим

П p и м e p 3 . Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов?

Р е ш е н и е. В соответствии с формулой (1.3.4) находим

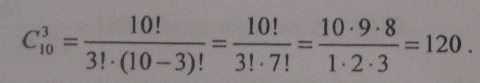
П р и м е р 4. Сколько различных шестизначных чисел можно записать с помощью цифр 1; 1; 1; 2; 2; 2?

Р е ш е н и е. Здесь нужно найти число перестановок с повтoрениями, которое определяется формулой (1.3.7). При k = 2, n1 = 3, n2 = 3, n=6 по этой формуле получаем

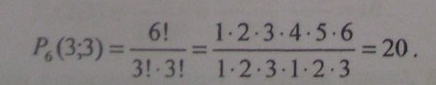
П р и м е р 5. Сколько различных перестановок букв можно сделать в словах замок, ротор, топор, колокол?

Р е ш е н и е. В слове замок все буквы различны, всего их пять. В оответствии c формулой (1.3.1) получаем

Р₅ =5!=1* 2* 3*4* 5=120.

B слове ротор, состоящем из пяти букв, буквы р и o повторяются дважды. Для подсчета различных перестановок применяем формулу (1.3.7). При n = 5, n1 = 2, n2 = 2 по этой формуле находим Р₅(2;2)=

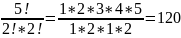
B слове топор буква o повторяется дважды, поэтому

Р₅(2)=

B слове колокол, состоящем из семи букв, буква к встречается дважды, буква o - трижды, буква л - дважды. B соответствии c формулой (1.3.7) при n = 7, n1, = 2, n2 = 3, n3 = 2 получаем

P₇(2;3;2)=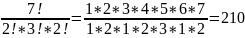

П p и м e p 6 . На пяти одинаковых карточках написаны буквы И, К, M, H, C. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность того, что получится слово МИНСК?

P е ш e н и e . Из пяти различных элементов можно составить Р₅ перестановок: Р₅ =1 *2*3 *4*5 =120 . Значит, всего равновозможных исходов будет 120, a благоприятствующих данному событию - только один. Следовательно,

formula

П р и м е р 7. Из букв слова ротор, составленного с помощью разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово тop?

P e ш e н и е . Чтобы отличить одинаковые буквы друг от друга, снабдим их номерами: р1, р2, о1, о2. Общее число элементарных исходов равно: A³₅ =5*4*3=60. Слово ротор получится в 1*2*2 = 4 случaяx (mo₁p₁, mo₁p₂,mo₂p₁,mo₂p₂). Искомая вероятнoсть равна

P= =

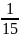
П р и м е р 1 4. Игральный кубик подбрасывают 10 раз. Какова вероятность того, что при этом грани 1, 2, 3, 4, 5, 6 выпадут соответственно 2, 3, 1, 1, 2 (событие А)?

Р е ш е н и е. Число исходов, благоприятных для события А подсчитаем по формуле (1.3.7):

m = 2 3 5 7 8 9 10;

Число элементарных исходов в данном опыте n , поэтому

P(А) 0,002

З а д а ч и

1. На 5 одинаковых карточках написаны буквы Б, Е, Р, С, Т. Эти карточки наудачу расположены в ряд. Какова вероятность того, что получится слово БРЕСТ?

2. В ящике 4 голубых и 5 красных шаров. Из ящика наугад вынимают 2 шара. Найдите вероятность того, что эти шары разного цвета.

3. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажутся 2 женщины и 2 мужчины?

4. В ящике 10 шаров, из которых 2 белых, 3 красных и 5 голубых. Наудачу извлечены 3 шара. Найдите вероятность того, что все 3 шара красного цвета.

5. На 5 одинаковых карточках написаны буквы л, м, о, о, т. Какова вероятность того, что извлекая карточки по одной наугад, получим в порядке их выхода слово молот?

6. Из партии, содержащей 10 изделий, среди которой 3 бракованных извлекают 3 изделия. Найдите вероятность того, что в полученной выборке одно изделие бракованное.

7. Из десяти билетов выигрышными являются два. Чему равна вероятность того, что среди взятых наудачу пяти билетов один выигрышный?

Ответы

1. 1/120. 2. 5/9. 3. 18/35. 4. 0,25. 5. 1/60. 6. 21/40. 7. 5/9.

Вопросы

1.Что называют перестановками?

2.По какой формуле вычисляют число перестановок из n различных элементов?

3. Что называют размещением?

4. По какой формуле вычисляют размещение из n различных элементов по m элементов?

5. Что называют сочетаниями?

6. По какой формуле вычисляют число сочетаний из n элементов по m элементов?

7. Каким равенством связаны числа перестановок, размещений и сочетаний?

8. По какой формуле вычисляют число перестановок из n элементов, если некоторые элементы повторяются?

9. Какой формулой определяется число размещений по m элементов с повторением из n элементов?

10. Какой формулой определяется число сочетаний с повторениями из n элементов по m элементов?