§ 3.4. Равномерное распределение.

Распределение вероятностей случайной величины Х называется равномерным на отрезке [α, β], если плотность вероятностей этой величины на данном отрезке постоянна и равна нулю вне этого отрезка:

(3.4.1)

С равномерным распределением встречаемся всякий раз, когда по условиям опыта величина Х принимает значения в конечном промежутке [α, β]. Все значения из этого промежутка возможны в одинаковой степени, причем ни одно из значений не имеет преимуществ перед другими. Вот примеры такого рода: 1) Х – время ожидания на стоянке автобуса (величина Х распределена на отрезке [0, l] где l – интервал движения между автобусами); 2) Х – ошибка при взвешивании случайно выбранного предмета, получающаяся из округления результата взвешивания до ближайшего целого числа (величина Х имеет равномерное распределение на отрезке [-0,5;0,5], где за единицу принята цена деления шкалы).

Двумерная случайная величина (X, Y) называется равномерно распределенной в области G, если плотность распределения этой величины постоянна в данной области и равна нулю вне ее:

(3.4.2)

Пример 1. Найти значение с в формуле (3.4.1), определяющей равномерное распределение.

Решение. Поскольку для плотности распределения р(x) должно выполняться условие (2.3.6), то

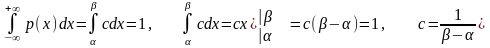
Следовательно, формула (3.4.1) принимает вид

Пример 2. Случайная величина Х равномерно распределена на отрезке [α , β] Найти вероятность попадания ее значений в интервал (γ, δ), принадлежащий отрезку [α, β].

Решение. Пользуясь формулой (2.3.3), находим

Поскольку δ – γ – длина интервала (γ, δ), и β – α - длина отрезка [α, β], то формула (3.4.4) выражает вероятность попадания в интервал (γ, δ) точки, брошенной в отрезок [α, β], т.е. геометрическое определение вероятности (см. формулу (1.5.3)).

Замечание 1. Выражение «выберем наудачу точку х на отрезке [α, β]» означает, что координата точки х представляет случайную величину с равномерным распределением вероятности на этом отрезке.

Пример 3. Найти значение С в формуле (3.4.2), определяющей равномерное распределение двумерной случайной величины (X, Y) в области G.

Решение. Вероятность попадания точки (X, Y) в любую область g, лежащую внутри области G, пропорциональна площади S_g области g:

Поскольку попадание в область G – достоверное событие, то

Откуда С=1/S_G. Подставляя это значение в первую формулу, получаем

Сравнивая эту формулу с формулой (1.5.1), заключаем, что получено геометрическое определение вероятности.

Замечание 2. Двумерная случайная величина (X, Y), где X, Y – координаты точки, наугад брошенной в область G, является равномерно распределенной в этой области.

Пример 4. Найти функцию распределения F(x) случайной величины Х, имеющей равномерное распределение.

Решение. Принимая во внимание формулу (2.3.2) и формулу (3.4.3) получаем: при х ≤ α

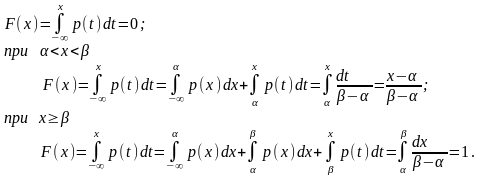
Итак, функция распределения имеет вид

Пример 5. Найти математическое ожидание случайной величины Х, имеющей равномерное распределение на отрезке [α, β].

Решение. Пользуясь формулой (2.4.8) и принимая во внимание формулу (3.4.3), находим

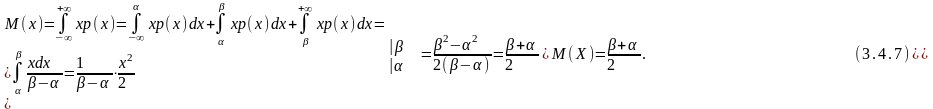
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке, есть середина этого отрезка.

Пример 6. Найти дисперсию случайной величины Х, имеющей равномерное распределение на отрезке [α, β].

Решение. Пользуясь формулой (2.5.15) и принимая во внимание формулы (3.4.3) и (3.4.7), находим

Пример 7. Случайная величина Х равномерно распределена на отрезке [2,7]. Записать плотность распределения p(x) этой случайной величины.

Решение. Плотность распределения р(х) случайной величины Х, равномерно распределенной на отрезке [α, β], определяется формулой (3.4.3). В данном случае α =2, β = 7, β - α =5; следовательно,

Пример 8. Случайная величина Х равномерно распределена на отрезке [-3;2]. Найти функцию распределения F(x) этой случайной величины.

Решение. Функция распределения F(x) случайной величины Х, равномерно распределенной на отрезке [α, β], определяется формулой (3.4.6). Из условия задачи следует, что α = -3, β = 2, β-α = 2-(-3) = 5; значит

Пример 9. Найти математическое ожидание случайной величины Х,

значения параметра λ>1, λ<1 ( при λ=1 получаем показательное распределение). В случае λ>1 кривая распределения имеет один максимум в точке х=(λ-1). В случае λ<1 плотность распределения убывает в интервале (0, +беск).

Пример1

Доказать, что вероятности дискретной случайной величины Х, определяемых формулой, удовлетворяют условию.

Решение

Запишем ряд, членами которого являются вероятности

Этот ряд является геометрическим рядом с первым членом р и значением q.

Геометрический ряд сходится, и его сумма равна:

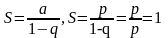
Итак,

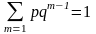
Пример 2

Найти математическое ожидание случайной величины Х, имеющей геометрическое распределение.

Решение

В соответствии получаем

Поскольку члены ряда являются производными, следовательно

Пример 3

Найти дисперсию случайной величины Х, имеющей геометрическое распределение.

Решение

Для вычисления дисперсии воспользуемся формулой:

Найдем сначала математическое ожидание квадрата величины Х:

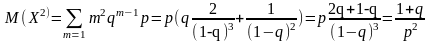
Таким образом,

Пример 4

Доказать, что функция удовлетворяет условию

Решение

Действительно,

Пример 5

Найти функцию распределения случайной величины, распределенной по показательному закону.

Решение

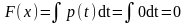
Если х>0, то

При х<0 F(х)=0

При х>=0 F(х)=1-е

Пример 6

Найти математическое ожидание случайной величины Х, имеющей показательное распределение.

Решение

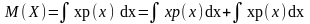
Применяя формулу по частям, получаем

Таким образом, математическое ожидание случайной величины, распределено по показательному закону, равно обратной величине параметра

Пример 7

Найти дисперсию и среднее квадратическое отклонение случайной величины, имеющей показательное распределение.

Решение

Дисперсию найдем по формуле

Используя формулу и результаты примера 6, выражение для дисперсии перепишем в виде

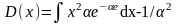
Дважды интегрируя по частям, получаем:

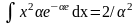
Следовательно,

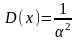
Замечание. Математическое ожидание и среднее квадратичное отклонение показательного распределения равны между собой.

Пример 8

Найти вероятность попадания в интервал (а,b) значений случайной величины Х, распределенной по показательному закону.

Решение

Воспользуемся функцией распределения и формулой

Р(а<X>b)=F(b)-F(а).

Т.к. 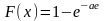при х>0 и F(х)=0 при х<=0,

То

Пример 9

Непрерывная величина Х распределена по показательному закону: р(х)=0 при х<0. найти вероятность попадания значений величины Х в интервал (0,1;0,7).

Решение

Поскольку а=2, то по формуле получим

Пример 10

Записать плотность распределения и функцию распределения показательного закона, если параметр а=7.

Решение

Согласно формуле записываем плотность распределения

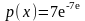при х<0

при х>=0

В соответствии с формулой находим функцию распределения

F(х)=0 при х<=0,

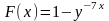при х>0

Пример 11

Найти математическое ожидание случайной величины Х, плотность распределения которой определяется функцией при х>=0

Решение

Поскольку в данном случае α=0,2 и , то

Пример 12

Найти дисперсию и среднее квадратическое отклонение случайной величины Х, плотность распределения которой задана функцией

Решение

Т.к. для показательного закона

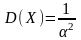
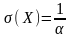
И по условию α=5, то

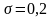
Пример 13

Производится подбрасывание игрального кубика до первого выпадения шести очков. Какова вероятность того, что первое выпадение шестерки произойдет при втором подбрасывании игрального кубика?

Решение

Воспользуемся формулой. Поскольку в данном случае р=1/6 (вероятность появления шестерки при подбрасывании кубика) и m=2, то

Пример 14

В партии из 12 деталей имеется 8стандартных. Найти вероятность того, что среди 5 взятых деталей окажется 3 стандартных.

Решение

Применяем формулу. Т.к. в данном случае N=12, М=8, n=5, m=3, то

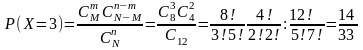
Задачи

1. В ящике 10 деталей, причем 7 стандартных. Какова вероятность того, что среди взятых наудачу деталей окажется 4 стандартных?

2. По какому закону распределена случайная величина Х, если плотность вероятностей этой величины определена функцией 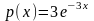при х>=0/

3. Найдите математическое ожидание случайной величины Х с плотностью распределения при х>=0/

4. Чему равна дисперсия случайной величины Х с плотностью распределения при х>=0.

5. Найдите среднее квадратическое отклонение случайной величины Х с плотностью распределения при х>=0.

6. Найдите функцию распределения случайной величины Х, если ее плотность определена функцией при х>=0.

7. Случайная величина Х распределена по показательному закону: р(х)=0 при х>0. найдите вероятность попадания значений этой величины в интервал (0,1;1).

8. Случайная величина Х распределена по показательному закону: р(х)=0 при х<0, при х>=0. Найдите математическое ожидание, дисперсию, среднее квадратичное отклонение и функцию распределения этой случайной величины.

9. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р=0,7. какова вероятность того, что попадание произойдет при третьем выстреле?

Ответы

1. 0,5 2. По показательному закону. 3. 2,5. 4. 1/16. 5. 2. 6. . 7. 0,691. 8. М(Х)=1/6, D(Х)=1/36, Р(0,2<Х<1.1)=0,512. 9. 0,063.

Вопросы

1. Какое распределение дискретной случайной величины называется геометрическим?

2. Чему равно математическое ожидание случайной величины, имеющей геометрическое распределение?

3. Чему равна дисперсия геометрически распределенной случайной величины?

4. Чему равно среднее квадратическое отклонение геометрически распределенной случайной величины?

5. Как определяется гипергеометрическое распределение случайной величины?

6. Как определяется показательное распределение случайной величины?

7. какой вид имеют функция распределения для показательного закона?

8. Каково соотношение между математическим ожиданием и средним квадратическим отклонением случайной величины, имеющей показательное распределение?

9. Чему равна дисперсия случайной величины, имеющей показательное распределение?

10. Как найти вероятность попадания в заданный интервал (а, b) значений случайной величины Х, имеющей показательное распределение?