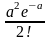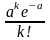§ 3.3 Распределение Пуассона

В одинаковых условиях производится n независимых испытаний, в каждом из которых может появиться событие А с вероятностью р или событие А¯ с вероятностью q(q=1- p). Вероятность того, что при n испытаниях событие А появится к раз ( и не появится n – к раз ) определяется формулой Бернулли (см. формулу (3.1.1)).

Рассмотрим случай, когда n является достаточно большим, а р – достаточно малым; положим np = а, где а – некоторое число.

Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой

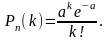(3.3.1)

Постоянную

a = np. (3.3.2)

входящую в формулу (3.3.1), называют параметром распределения Пуассона.

Закон распределения Пуассона можно записать в виде следующей таблицы:

Х	0	1	2	…	К	…
Р	е-а	ае-а		…		…

Пример 1. Доказать, что распределение Пуассона является предельным случаем биномиального распределения.

Решение. Из равенства ( 3.3.2) определим p и q :

,

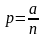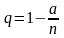
и подставим в формулу Бернулли:

Переходя к пределу при n > ∞, получаем

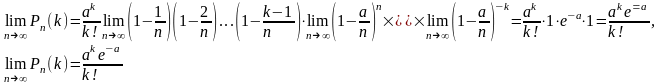
(3.3.3)

Итак, формула (3.3.1), определяющая распределение Пуассона, является предельным случаем формулы Бернулли, которой определяется биномиальное распределение.

Пример 2. Доказать, что

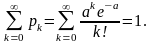(3.3.4)

Решение. Принимая во внимание разложение функции 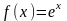в степенной ряд

и вытекающее отсюда равенство

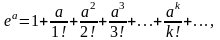
получаем

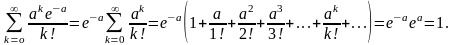
Таким образом, ряд из вероятностей распределения Пуассона сходится и его сумма равна единице, т. е. выполняется условие (2.1.4) в определении закона распределения дискретной случайной величины.

Пример 3. Найти математическое ожидание дискретной случайной величины, распределенной по закону Пуассона.

Решение. На основании таблицы, определяющей закон распределения, и формулы (2.4.6) находим

Итак, математическое ожидание случайной величины, распределенной по закону Пуассона, равно числу а – параметру этого распределения.

Пример 4. Найти дисперсию дискретной случайной величины, имеющей распределение Пуассона.

Решение. Дисперсию вычисляем по формуле (2.5.4), для чего вначале найдем математическое ожидание квадрата данной величины:

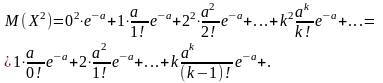
Положив к – 1 = m, получим

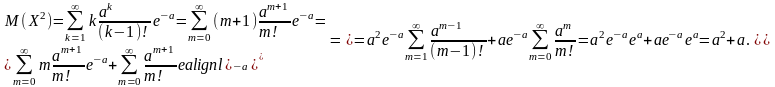
По формуле (2.5.4) находим дисперсию:

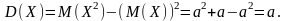
Таким образом,

D(X) = a (3.3.6)

т.е. дисперсия случайной величины, распределенной по закону Пуассона, равна числу а – параметру этого распределения.

Пример 5. Доказать, что сумма двух независимых случайных величин, распределенных по закону Пуассона с параметрами a и b ,также распределена по закону Пуассона с параметром a + b.

Решение. По условию для случайных величин X и Y

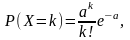
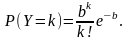
Поскольку случайные величины X и Y независимы, то случайные события (X=m) и (Y=k - m) независимы при любых целых неотрицательных k и m, 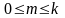, поэтому

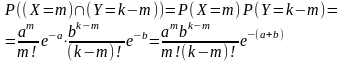
По формуле полной вероятности получаем

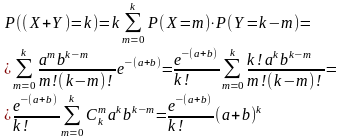
Таким образом,

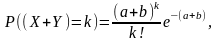(3.3.7)

т.е случайная величины (X+Y) распределена по закону Пуассона с параметром a+b

Замечание. Формула (3.3.7) распространяется на n независимых величин, распределенных по закону Пуассона.

Пример 6. Случайная величина Х распределена по закону Пуассона. Найти Р(Х=3) ,если а = 4, а также математическое ожидание и дисперсию величины Х.

Решение. По формуле (3.3.1) находим

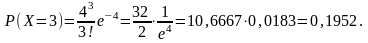
Согласно формулам (3.3.5) и (3.3.6) получаем

М(Х)=4, D(X)=4.

Пример 7. Производятся независимые испытания, в каждом из которых событие А может появиться с вероятностью р = 0,002. Какова вероятность того, что при 1000 испытаниях событие А появится 5 раз?

Решение. Воспользуемся формулой (3.3.1). По условию п = 1000, р = 0,002, к = 5. Так как а = пр = 1000*0,002 = 2 (см. формулу (3.3.2)), то

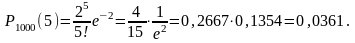
Пример 8. Случайная величина Х распределена по закону Пуассона с параметром а = 3, случайная величина Y распределена по закону Пуассона с параметром b = 2; эти случайные величины независимы. Найти закон распределения их сумм.

Решение. В соответствии с формулой (3.3.7) получаем

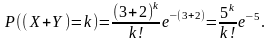
Пример 9. Вероятность изготовления нестандартной детали р = 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.

Решение. Здесь п = 1000, р = 0,004, а = пр = 1000*0,004 = 4. По формуле (3.3.1) находим

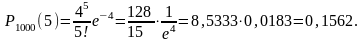
Пример 10. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течении 1 мин. равна 0,002. Найти вероятность того, что в течении 1 мин. обрыв произойдет более чем на трех веретенах.

Решение. В соответствии с условием имеем: п = 1000, р = 0,002, а = пр = 1000*0,002 = 2, k > 3.

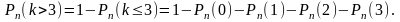
Применяя формулу (3.3.1), находим:

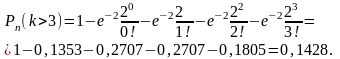
Пример 11. Производятся независимые испытания, в каждом из которых событие А может появиться с вероятностью, равной 0,001. Какова вероятность того, что при 2000 испытаниях событие А появится не менее двух и не более четырех раз.

Решение. Из условия задачи следует, что п = 2000, р = 0,001, а = пр = 2000*0,001 = 2, 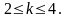Следовательно

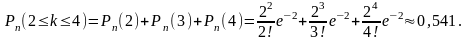
Пример 12. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Какова вероятность того, что на базу прибудут 3 негодных изделия?

Решение. Из условия следует, что п = 5000, р = 0,0002, а = пр = 5000*0,0002 = 1. Согласно формуле (3.3.1) имеем

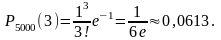
Пример 13. Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух элементов? Какова вероятность отказа не менее двух элементов за год?

Решение. Здесь требуется найти вероятности: 1) Р₁₀₀₀(2); 2) Р₁₀₀₀(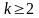 ). По условию п = 1000, р = 0,001, а = пр = 1000*0,001 = 1.

Вероятность отказа ровно двух элементов:

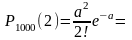
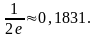
Вероятность отказа не менее двух элементов:

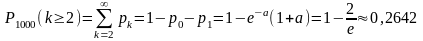
Пример 14 Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию, равна 0, 01. Найти вероятность следующих событий: «в течение часа 5 абонентов позвонят на станцию»; «в течении часа не более 4 абонентов позвонят на станцию»; «в течении часа не менее 3 абонентов позвонят на станцию»;

Решение: Согласно условию п = 400, р = 0,01, тогда а = пр = 400*0,01 = 4.

В соответствии с формулой (3.3.1) находим

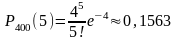
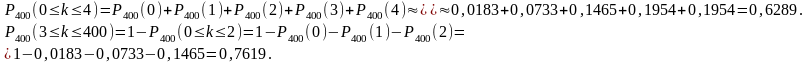
Пример 15. Производится независимое испытание, в каждом из которых может появится событие А с вероятностью р = 0,01. Найти вероятность того, что при 100 испытаниях событие А появится соответственно 1, 2, 3, 4, 5, 6 раз, не появится ни разу.

Решение. При подсчете искомых вероятностей будем пользоваться рекуррентной формулой

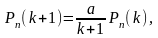(3.3.8)

которая получается следующим образом:

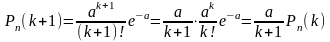
При а = 1 эта формула принимает ид

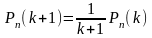(3.3.9)

Если известна вероятность Р_п(0), то по формуле (3.3.9) можно вычислить Р_п(1), Р_п(2), Р_п(3) и т.д.

Из условия задачи следует, что п = 100, р = 0,01, поэтому

а = пр = 100*0,01 = 1. По формуле (3.3.1) находим

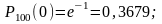
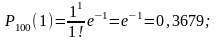
Пользуясь формулой (3.3.9) последовательно получаем:

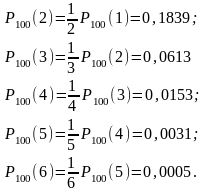
Пример 16. На факультете обучается 500 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно для к студентов данного факультета? Вычислить эту вероятность для значений к = 0, 1, 2, 3.

Решение. Поскольку п = 500 является достаточно большим, а р = 1/365 – достаточно малым, то можно считать, что случайная величина Х студентов, родившихся 1 сентября, подчиняется закону распределения Пуассона с параметром а = пр = 500/365 = 1,36986.

По формуле (3.3.1) получаем р₀ = Р(Х=0) = е^-а = 0,2541. Пользуясь формулой (3.3.8), последовательно находим:

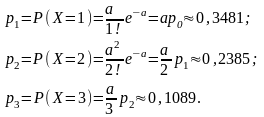
Пример 17. При введении вакцины против полиомиелита иммунитет создается в 99,99% случаев. Какова вероятность того, что из 1000 вакцинированных детей заболеет соответственно 1, 2, 3, 4 ребенка?

Решение. Вероятность заболеть р = 0,0001, число испытаний п = 10000, поэтому а = пр = 1. По формуле (3.3.1) находим:

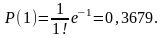
В соответствии с формулой (3.3.8) получаем:

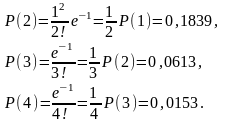
Задачи

1. Производятся независимые испытания, в каждом из которых событие А может появится с вероятностью р = 0,0015. Какова вероятность того, что при 2000 испытаниях событие А появится 3 раза?

2. Независимые случайные величины X и Y распределены по закону Пуассона: величина X – с параметром а = 4, величина Y – с параметром

b = 3. Найдите закон распределения их суммы.

3. Известно, что в принятой для сборке партии из 1000 деталей имеются 4 дефектных. Найти вероятность того, что среди 50 наугад взятых деталей нет дефектных.

4. Завод отправил на базу 5000 качественных изделий. Вероятность повреждения в пути каждого изделия равна 0,0002. Найти вероятность того, что среди 5000 изделий в пути будет повреждено: а) ровно 3 изделия; б) ровно одно изделие; в) не более 3 изделий; г) более 3 изделий.

5. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозки бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит: а) хотя бы одну; б) менее 2; в) ровно 2; г) более 2 разбитых бутылок.

6. Независимые случайные величины X, Y, Z распределены по закону Пуассона соответственно с параметрами а = 1, b = 2, с = 3. Найти закон распределения их суммы.

7. Независимые случайные величины X, Y, Z распределены по закону Пуассона, причем М(Х) = а, M(Y) = b, M(Z) = c. Найти закон распределения их суммы и M(X+Y+Z).

8. Независимые случайные величины X_k (k = 1, 2, …. m) распределены по закону Пуассона, причем М(Х_к) = а_к. Запишите закон распределения их суммы.

Ответы

1. 0,2242. 2. 7^ке^-7/к! 3. 0,8187. 4. а) 0,06313; б) 0,367879; в) 0,981011;

г) 0,018989. 5. а) 0,95; б) 0,1992; в) 0,224; г) 0, 577. 6.

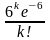
7. 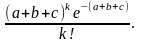8.

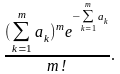
Вопросы

1. Почему закон распределения Пуассона называют законом редких событий?

2. При каких условиях можно применять закон распределения Пуассона?

3. Запишите формулу Пуассона и объясните смысл каждого символа.

4. Что является случайной величиной в законе Пуассона?

5. Каковы общие условия, необходимые для применимости закона распределения Пуассона и закона биномиального распределения?

6. Как связаны между собой биномиальное распределение и распределение Пуассона?

7. Чему равны математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона?

8. Какая из величин в законе Пуассона больше: математическое ожидание или число независимых испытаний?

9. Исследуется распределение Пуассона. Что вероятнее: событие А появится ровно один раз или ни разу?