- •II. Pamięci
- •Pojedyncza I sieć jednostek pamięci (o wielu wejściach) zbudowanych na bramkach or
- •Komórka pamięci o pojemności 1 bit, po lewej sram, po prawej dram
- •Porównanie parametrów urządzeń pamięci
- •Struktura logiczna 1-bitowej komórki pamięci
- •Schemat (I symbol) fizycznej jednostki pamięci I jej łączy z zewnętrzem
- •Tablica wartości modułu sterującego pamięci
- •Przykład adresów I zawartości sześciu spośród 210 słów pamięci
- •Dekodowanie I demultipleksowanie adresów na kości dram 64k
- •Schemat logiczny pamięci rom
- •Struktura logiczna pamięci rom 25×8
- •Tabela wartości dekodera
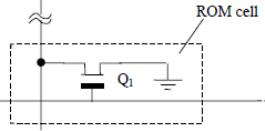
- •Komórka pamięci rom – (Metal Oxide Semiconductor)
- •Typowa organizacja pamięci podręcznej
- •Przykład odwzorowania bloków pamięci ram na linie pamięci podręcznej
Tabela wartości dekodera
Zarówno dekoder jak i pamięć właściwa są urządzeniami działającymi zgodnie z regułami algebry Boola. Wobec tego wartości zmiennych logicznych na wyjściu są pewnymi funkcjami logicznymi wartości zmiennych na wejściu. Dotychczas układ scalony pamięci opisywaliśmy tablicą wartości, poprzednie dwa zdania sugerują, że można go również opisać zbiorem funkcji logicznych. W praktyce programowanie pamięci ROM odbywa się za pomocą odpowiednich urządzeń sterowanych wyspecjalizowanym programem komputerowym. Danymi dla tego programu jest tablica wartości. W pewnych wypadkach ogólną tablicę wartości k×2k n można uprościć, redukując koszt wytworzenia chipu. Można tego dokonać analizując funkcje logiczne wyjść w postaci sumy mintermów wejść. Dokonamy tego na prostym przykładzie.
Przykład
Zaprojektować pamięć przechowującą kwadraty liczb całkowitych od 0 do 7.
Z poprzedniej ogólnej analizy wynika, że dekoder musi otrzymać trzy liczby (na wyjściu z niego otrzymamy 23 = 8 adresów) a pamięć musi mieć 6 wyjść (gdyż 25 < 72 <26). Całkiem ogólna tablica wartości dla obwodów kombinacyjnego ma postać
wejścia |
wyjścia |
||||||||
A2 |
A1 |
A0 |
B5 |
B4 |
B3 |
B2 |
B1 |
B0 |
dziesiętnie |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
4 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
9 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
16 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
25 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
36 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
49 |
W celu ewentualnego uproszczenia pamięci należy poddać analizie funkcję w postaci sumy mintermów każdego wyjścia.
wyjście B0:
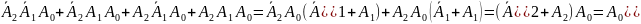
wyjście B1:

.
.
wyjście B5:

Widać, że wyjście B1 ma stałą wartość niezależną od wejścia, a wyjście B0 jest identyczne z wejściem A0. Ta kość będzie miała prostszą konstrukcję i będzie tańsza. Teraz możemy podać schemat i tablicę wartości minimalnej struktury przechowującej to co chcemy.
wejścia |
wyjścia |
||||||
A2 |
A1 |
A0 |
B5 |
B4 |
B3 |
B2 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
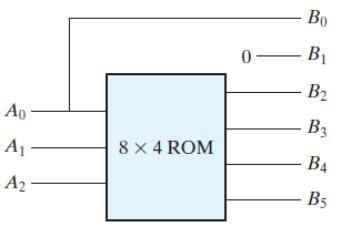
Schemat logiczny Tablica wartości
Uproszczenie funkcji
każdego z powyższych czterech wyjść jest możliwe. Na przykład
funkcja opisująca wyjście B2 ma postać
 .
Odpowiada jej bramka
.
Odpowiada jej bramka

Znając wszystkie cztery funkcje moglibyśmy zamówić wykonanie takiej wyspecjalizowanej kości u producenta. Postępowanie takie byłoby zazwyczaj niecelowe, gdyż koszt wytworzenie jednego egzemplarza takiej kości byłby wysoki. Bardziej opłacalne dla nabywców pojedynczych egzemplarzy będzie zakupienie kości o zadanych liczbach k i n (liczbach wejść i wyjść) a następnie zaprogramowanie jej do wykonywania takich czynności jakimi jest zainteresowany klient.
Fizyczna realizacja pamięci ROM