Реальные газы.

39.Отступление от законов идеальных газов. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.

При увеличении плотности (давления) поведение газа все сильнее отличается от поведения идеального газа. Это объясняется тем, что при малых средних расстояниях между молекулами все большее значение приобретают силы межмолекулярного взаимодействия. На малых расстояниях эти силы являются силами отталкивания, а на больших – силами притяжения. Влияние этих сил на вид уравнения состояния можно приближенно учесть следующим образом. Для реальных газов давление должно резко возрастать при конечном объеме, равном по порядку величины объему всех частиц газа. Обозначим этот конечный объем для одного моля через b, тогда давление газа может быть записано в виде

.

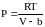Действие сил притяжения между молекулами проявляется в уменьшении давления газа по сравнению с приведенной величиной. Уменьшение давления связано с тем, что на молекулу, находящуюся у стенки сосуда, действует сила, направленная внутрь сосуда. Она обусловлена притяжением со стороны молекул газа, находящихся в его объеме. В первом приближении ее величина пропорциональна концентрации молекул

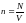, а, учитывая, что давление само пропорционально концентрации, поправка на уменьшение давления будет пропорциональна .

Учитывая это, можно прийти к соотношению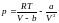 ,которое в форме

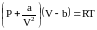называется уравнением Ван-дер-Ваальса (для одного моля газа). Поправки a и b – постоянные Ван-дер-Ваальса, учитывающие соответственно действие сил притяжения и отталкивания между молекулами газа.

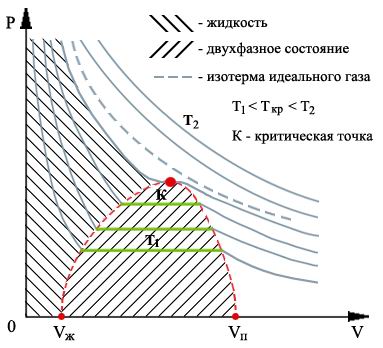
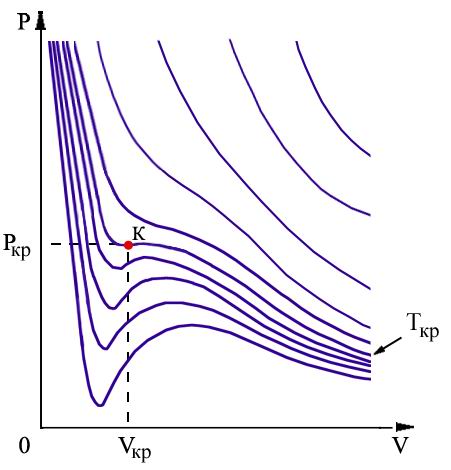
Ниже на рисунке схематически изображены изотермы газа Ван-дер-Ваальса для различных температур.

40.Сравнение изотерм Ван-дер-Ваальса с экспериментальными. Критическое состояние. Фазовые переходы 1 и 2 рода. Фазовые диаграммы. Тройная точка.

Схематически изображения изотерм газа Ван-дер-Ваальса для различных температур.

На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма при одинаковых значениях параметров и . При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К). Эта точка называется критической, а значения , и в этой точке называются критическими параметрами. При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями .

Критические параметры , и можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба:

,
,
.

Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами , и , величина которых зависит от свойств газа.

Обратимся теперь к экспериментальным обоснованиям уравнения состояния газа Ван-дер-Ваальса. На рис 2. показан вид экспериментально полученных изотерм, характерный для многих веществ.

Рис. 2.. Изотермы реального газа

На этих кривых виден горизонтальный участок, который заменяет немонотонный участок на изотермах газа Ван-дер-Ваальса. Справа от горизонтального участка экспериментальная изотерма монотонно растет с уменьшением объема, что соответствует сжатию реального газа при постоянной температуре. Горизонтальный участок соответствует сжижению газа, которое при заданной температуре происходит при постоянном давлении. При этом существует двухфазная система жидкость-газ. Наконец, слева от горизонтального участка, где изотерма вновь становится монотонно убывающей функцией , весь газ превращается в жидкость. При этом давление очень резко растет с уменьшением объема. Это связано с тем, что размеры молекул жидкостей становятся сравнимы с межмолекулярными расстояниями. Этот участок экспериментальных изотерм наиболее сильно отличается от предсказываемого уравнением для газа Ван-дер-Ваальса.

Термодинамическая фаза— термодинамически однородная по составу и свойствам часть термодинамической системы, отделенная от других фаз поверхностями раздела, на которых скачком изменяются некоторые свойства системы. В однокомпонентной системе разные фазы могут быть представлены различными агрегатными состояниями или разными полиморфными модификациями вещества. В многокомпонентной системе фазы могут иметь различный состав и структуру.

Термодинамические фазы на фазовой диаграмме

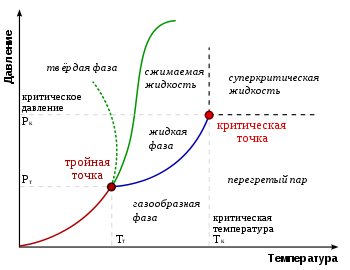
Типичные виды фазовых диаграмм. Зелёная линия из точек показывает аномальное поведение воды

На фазовой диаграмме вещества различные термодинамические фазы занимают определённые области. Линии, разделяющие различные термодинамические фазы, называются линиями фазового перехода. Если вещество находится в условиях, отвечающих точке внутри какой-либо области, то оно полностью находится в этой термодинамической фазе. Если же состояние вещества отвечает точке на одной из линий фазовых переходов, то вещество в термодинамическом равновесии может находиться частично в одной, а частично в другой фазе. Пропорция двух фаз определяется, как правило, полной энергией, запасённой системой.

При медленном (адиабатическом) изменении давления или температуры вещество описывается движущейся точкой на фазовой диаграмме. Если эта точка в своём движении пересекает одну из линий, разделяющих термодинамические фазы, происходит фазовый переход, при котором физические свойства вещества меняются скачкообразно.

Не все фазы полностью отделены друг от друга линией фазового перехода. В некоторых случаях эта линия может обрываться, оканчиваясь критической точкой. В этом случае возможен постепенный, а не скачкообразный переход из одной фазы в другую, в обход линии фазовых переходов.

Точка на фазовой диаграмме, где сходятся три линии фазовых переходов, называется тройной точкой. Обычно под тройной точкой вещества подразумевается частный случай, когда сходятся линии плавления, кипения и сублимации, однако на достаточно богатых фазовых диаграммах может быть несколько тройных точек. Вещество в тройной точке в состоянии термодинамического равновесия может частично находиться во всех трёх фазах. Набор термодинамических фаз вещества обычно значительно богаче набора агрегатных состояний, т.е. одно и то же агрегатное состояние вещества может находиться в различных термодинамических фазах. Именно поэтому описание вещества в терминах агрегатных состояний довольно огрублённое, и оно не может различить некоторые физические разные ситуации.

(Фазовые переходы типа диссоциации молекул или ионизации являются, по определению, переходами одного вещества в другое).

Классификация фазовых переходов. При фазовом переходе первого рода скачкообразно изменяются самые главные, первичные экстенсивные параметры: удельный объём (т.е. плотность), количество запасённой внутренней энергии, концентрация компонентов и т.п. Подчеркнём: имеется в виду скачкообразное изменение этих величин при изменении температуры, давления и т. п., а не скачкообразное изменение во времени (насчёт последнего см. ниже раздел Динамика фазовых переходов).

Наиболее распространённые примеры фазовых переходов первого рода:

плавление и затвердевание, кипение и конденсация, сублимация и десублимация

При фазовом переходе второго рода плотность и внутренняя энергия не меняются, так что невооружённым глазом такой фазовый переход может быть незаметен. Скачок же испытывают их вторые производные по температуре и давлению: теплоёмкость, коэффициент теплового расширения, различные восприимчивости и т.д.

Фазовые переходы второго рода происходят в тех случаях, когда меняется симметрия строения вещества (симметрия может полностью исчезнуть или понизиться). Описание фазового перехода второго рода как следствие изменения симметрии даётся теорией Ландау.

Наиболее распространённые примеры фазовых переходов второго рода:

прохождение системы через критическую точку

переход парамагнетик-ферромагнетик или парамагнетик-антиферромагнетик (параметр порядка — намагниченность)

переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата)

переход жидкого гелия в сверхтекучее состояние (п.п. — плотность сверхтекучей компоненты)

переход аморфных материалов в стеклообразное состояние

Тройная точка— точка на фазовой диаграмме, где сходятся три линии фазовых переходов. Тройная точка — это одна из характеристик химического вещества. Обычно тройная точка определяется значением температуры и давления, при котором вещество может равновесно находится в трёх (отсюда и название) агрегатных состояниях — твёрдом, жидком и газообразном. В этой точке сходятся линии плавления, кипения и сублимации.

В более общем случае могут рассматриваться и другие фазы вещества, не соответствующие различным агрегатным состояниям. На достаточно богатых фазовых диаграммах может быть несколько тройных точек. Вещество в тройной точке в состоянии термодинамического равновесия может частично находиться во всех трёх фазах. На многомерных фазовых диаграммах (то есть если кроме температуры и давления присутствуют иные интенсивные величины) могут существовать четверные и т.д. точки.