Основы термодинамики.

33.Термодинамическая система и термодинамические параметры. Равновесные состояния и процессы. Обратимые и необратимые процессы. Изопроцессы и их изображение на термодинамических диаграммах.

Термодинамическая система – часть пространства, выделенная для рассмотрения и отделенная от окружающей среды реальной (межфазовой) или условной границей. Системы могут быть изолированными, закрытыми (замкнутыми) и открытыми. Изолированная система характеризуется постоянством массы m, объема V, энергии U (m=соnst, V= соnst, U= соnst) она не обменивается с окружающей средой ни веществом, ни энергией. Закрытая система обменивается с окружающей средой только энергией и не обменивается веществом (m= соnst, V не соnst, U не соnst). В открытой системе осуществляются оба указанных вида обмена с окружающей средой (m не const, V не соnst, U не соnst).

Состояние системы определяется ее физическими и химическими свойствами (объем, давление, температура, химический состав, внутренняя энергия, энтальпия, энтропия и др.), которые подразделяются на параметры состояния и функции состояния. Параметры состояния – свойства системы, выбранные в качестве независимых переменных. (объем, давление, температура).

Равновесный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний. Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений. Примеры равновесных процессов(изотермический процесс, изохорный процесс, изобарный процесс, адиабатический процесс).

Обратимыми называются термодинамические процессы, осуществление которых возможно в прямом и обратном направлениях, при том так, что в обратном процессе термодинамическая система проходит через те же равновесные промежуточные состояния, что и в прямом процессе, но только в обратной последовательности. Обязательным условием для протекания обратимых процессов является соблюдение механического равновесия (равенство давлений), теплового равновесия (равенство температур), и отсутствие трения.

Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, термодиффузия, теплопроводность, вязкое течение и др.

Изобарный процесс - процесс изменения состояния термодинамической системы при постоянном давлении ( )

Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

Изохорный процесс - процесс изменения состояния термодинамической системы при постоянном объёме ( ). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:

Линия, изображающая изохорный процесс на диаграмме, называется изохорой.

Изотермический процесс - процесс изменения состояния термодинамической системы при постоянной температуре ( )(). Изотермический процесс описывается законом Бойля - Мариотта:

34.Работа в термодинамике (работа газа в различных процессах).

Найдем работу, совершаемую газом при изменении его объема. Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде.

Е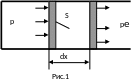 сли газ, расширяясь, передвигает поршень на расстояние dx, то он производит работу против сил внешнего давления р_е:

,где S  площадь поршня, dV  изменение объема газа. Полная работа А₁₂, совершаемая газом при изменении его объема от V₁ до V₂:

.

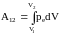Если процесс расширения газа является равновесным, т.е. идущим без перепадов давлений и температур, то работа может быть вычислена через давление самого газа (р_е=р). Графически работа газа равна площади под кривой процесса на диаграмме PV (рис.2). Если газ совершает круговой процесс (цикл), то работа будет равна площади цикла.

Работа газа при изопроцессах:

1) изохорический

V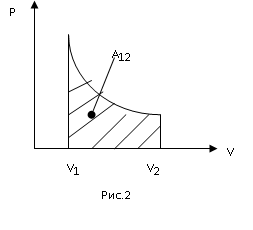 =const, dV=0, A₁₂=0;

2) изотермический T=const,

;

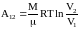3) изобарический р=const,

35.Способы изменения внутренней энергии. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам и адиабатическому процессу идеального газа.

Способы изменения внутренней энергии - теплопередача и работа.

Первое начало термодинамики - количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил.

.

Для элементарного количества теплоты, элементарной работы и малого приращения (полного дифференциала) внутренней энергии первый закон термодинамики имеет вид: .

Изохорический процесс (V = const). Газ не совершает работу, т.е. A=0. Из первого начала термодинамики следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: .

Изобарический процесс (p = const). Теплота, сообщаемая газу, идет на приращение внутренней энергии и на совершение работы над внешними телами:

.

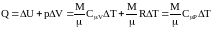Изотермический процесс (T = const). Внутренняя энергия газа не изменяется и все количество тепла, сообщаемое газу, расходуется на совершение им работы против внешних сил:

.

Адиабатическим называется процесс, при котором отсутствует теплообмен

(Q = 0) между физической системой и окружающей средой. Из первого начала термодинамики для адиабатического процесса следует, что 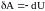, т.е. работа совершается за счет убыли внутренней энергии системы.

.

36.Зависимость теплоёмкости идеального газа от вида процесса.

Теплоемкость тела

В изотермическом процессе 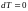, тогда .

В изохорном процессе постоянен объём, то есть . Элементарная работа газа равна произведению изменения объёма на давление, при котором происходит изменение ( ). Первое начало термодинамики для изохорного процесса имеет вид:

А для идеального газа

Таким образом,

- молярная теплоемкость газа при постоянном объеме.

где — число степеней свободы частиц газа.

В изобарном процессе постоянно давление, то есть р=соnst. Первое начало термодинамики для изобарного процесса имеет вид:

.

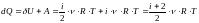- молярная теплоемкость газа при постоянном давлении.

где — число степеней свободы частиц газа.

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть . Однако, объём, давление и температура меняются, то есть .

Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: .

37.Круговой процесс (цикл). Тепловые двигатели и холодильные машины. Цикл Карно и его КПД для идеального газа. Независимость КПД цикла Карно от природы рабочего тела.

К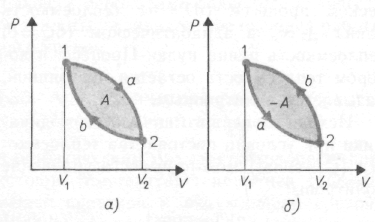 руговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (см.рис. a). Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1–2) и сжатия (2–1) газа. Работа расширения A₁ (определяется площадью фигуры 1 a 2 V₁ V₂ 2) положительна (dV>0)), работа сжатия A₂ (определяется площадью фигуры 1 a 2 V₁ V₂ 2) отрицательна (dV<0), Следовательно, работа A= A₁+ A₁, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл совершается положительная работа A>0 (цикл протекает по часовой стрелке), то он называется прямым (рис., а), если за цикл совершается отрицательная работа A<0 (цикл протекает против часовой стрелки), то он называется обратным (рис. b).

Прямой цикл используется в тепловых двигателях – периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах -периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.

В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю ( U = 0). В общем случае при протекании кругового процесса система может теплоту как получать Q₁, так и отдавать Q₂, поэтому теплота, полученная системой Q равна

Q=Q₁–Q₂

Поэтому из первого начала термодинамики для кругового процесса (когда U= 0) получаем, что работа за цикл равна

А=Q₁–Q₂ т. е. работа, совершаемая за цикл, равна разности количества полученной извне теплоты Q₁ и отданной системой Q₂. Поэтому коэффициент полезного действия для кругового процесса (к. п. д.)

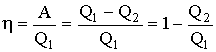
П ринцип действия теплового двигателя приведен на рисунке. От термостата с более высокой температурой Т₁, называемого нагревателем, за цикл отнимается количество теплоты Q₁, а термостату с более низкой температурой T₂ , называемому холодильником, за цикл передается количество теплоты Q₂, при этом совершается работа A = Q₁ - Q₂.

Чтобы коэффициент полезного действия теплового двигателя  = 1-Q₂/Q₁ был равен единице ( = 1), должно быть выполнено условие Q₂ = 0, т. е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Так, французский физик и инженер Н. Л. С. Карно (1796—1832) показал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами.Этот результат положен в основу одной из формулировок второго начала термодинамики по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода – периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты,— невозможен. Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип действия которой представлен на рисунке выше. Системой за цикл от термостата с более низкой температурой Т₂ отнимается количество теплоты Q₂ и отдается термостату с более высокой температурой Т₁количество теплоты Q₁. Для кругового процесса, согласно 1), Q = А, но, по условию, Q = Q₂ - Q₁ <0, поэтому А < 0 и Q₂ - Q₁ = – А, или Q₁ = Q₂+A, т.е. количество теплоты Q₁, отданное системой источнику теплоты при более высокой температуре Т₁, больше количества теплоты Q₂, полученного от источника теплоты при более низкой температуре Т₂ , на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому.

Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (Т₁) и холодильников (Т₂), наибольшим к. п. д. обладают обратимые машины; при этом к. п. д. обратимых машин, работающих при одинаковых температурах нагревателей (Т₁) и холодильников (Т₂), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами).

К арно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат, и называемый циклом Карно. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

Цикл Карно изображен на рисунке, где изотермические расширение и сжатие заданы соответственно кривыми 1–2 и 3–4, а адиабатические расширение и сжатие – кривыми 2–3 и 4-1.

К.п.д. цикла Карно определяется только температурами нагревателя и холодильника.

Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм. Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.

38.Энтропия. Принцип возрастания энтропии. Выражение энтропии системы через термодинамически вероятность состояния (формула Больцмана).

Энтропия системы – функция ее состояния. Приращение энтропии равно приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из начального состояния в конечное по любому обратимому процессу.

, .

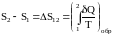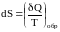Важной особенностью энтропии является ее возрастание в изолированных системах (закон возрастания энтропии): «Энтропия теплоизолированной (адиабатической) системы не может убывать; она возрастает, если в системе идет необратимый процесс, и остается постоянной при обратимом процессе в системе».

Необратимые процессы в системе приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума и в дальнейшем никакие макроскопические процессы в системе невозможны.

Изменение энтропии при наличии теплообмена с окружающей средой, может быть каким угодно: как больше нуля, так и меньше нуля.

Cогласно Больцману, энтропия cиcтемы и термодинамическая вероятность связаны между собой следующим образом:

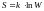
где — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть осуществлено данное макросостояние. Значит, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. Действительно, чем больше число микросостояний, которые реализуют данное макросостояние, тем больше энтропия. В состоянии равновесия - наиболее вероятного состояния системы - число микросостояний максимально, при этом также максимальна и энтропия.

Так как реальные процессы необратимы, то можно говорить, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, другими словами, от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной.