Основы мкт.

24.Макросистема и макропараметры. Состояние системы. Равновесное состояние. Принцип детального равновесия. Идеальный газ. Уравнение состояния идеального газа.

Система, состоящая из большого числа молекул, называется макросистемой. Макросистема, отделенная от внешних тел стенками с постоянными свойствами, после длительного промежутка времени приходит в равновесное состояние. Это состояние можно описать рядом параметров, называемых Параметрами состояния. Различают микропараметры и макропараметры состояния.

К микропараметрам состояния можно отнести следующие физические величины: массу молекул, их скорость, среднюю квадратичную скорость молекул, среднюю кинетическую энергию молекул, среднее время между соударениями молекул, длину их свободного пробега и др. Это такие параметры, которые можно отнести и к одной молекуле макросистемы.

Макропараметры состояния характеризуют только равновесную систему в целом. К ним относятся объем V, давление P, температура T, плотность, концентрация n, внутренняя энергия U, электрические, магнитные и оптические параметры. Значения этих параметров могут быть установлены с помощью измерительных приборов.

Молекулярно-кинетическая теория идеального газа устанавливает соответствие между микропараметрами и макропараметрами газа.

Состояние системы - это совокупность значений ее параметров (свойств) в определенный момент времени.

Равновесное состояние - состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура, давление, объём, энтропия) в условиях изолированности от окружающей среды.

Принцип детального равновесия — общее положение статистики, справедливое для многих случайных процессов и физических систем, находящихся в состоянии термодинамического равновесия. Его суть заключается в равенстве вероятностей прямого и обратного переходов между дискретными состояниями системы.

Идеальный газ — математическая модель газа, в которой предполагается, что: 1) потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объем молекул газа пренебрежимо мал. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением р, объёмом V и абсолютной температурой T идеального газа. Уравнение имеет вид:

, R=N_Ak=8,31 Дж/(мольК) – универсальная газовая постоянная.

где М – масса газа,  – молярная масса газа.

25.Вывод уравнения молекулярно-кинетической теории идеальных газов для давления и его сравнение с уравнением Клапейрона-Менделеева.

Давление газа на стенки сосуда можно рассматривать как ряд быстро следующих ударов газовых молекул о стенку. Рассмотрим, как вычислить давление, вызванное отдельными ударами. Представим себе, что по некоторой поверхности происходит ряд отдельных и частых ударов. Найдем такую среднюю постоянную силу , которая, действуя в течение времени t, за которое происходили отдельные удары, произведет такое же действие, как и все эти удары в своей совокупности. В таком случае импульс этой средней силы за время t должен равняться сумме импульсов всех тех ударов, которые получила поверхность за это время, т.е.

, где t₁, t₂, t₃ ... t_n - время взаимодействия первой, второй, ..., n-й молекул со стенкой (т.е. длительность удара); f₁, f₂, f₃ ... f_n - силы удара молекул о стенку. Из этой формулы следует, что , (7)

Средняя сила давления, вызванная рядом отдельных ударов о некоторую поверхность, численно равна сумме импульсов всех ударов, полученных этой поверхностью за единицу времени.

Найдем среднюю силу давления , возникающую вследствие ударов газовых молекул о стенки сосуда. Имеем сосуд в форме куба (рис. 4) с длиной ребра l, в котором движется n молекул, причем масса каждой молекулы равна m0. В результате хаотического движения молекул можно утверждать, что результат их ударов о стенки будет такой же, как будто 1/3 все молекул движется вдоль оси X, ударяя в правую и левую грани, 1/3 - движется вдоль оси Y, ударяя в переднюю и заднюю грани, а 1/3 - вдоль оси Z, ударяя в верхнюю и нижнюю грани.

Рис. 4

Найдем импульс силы, от удара одной (первой) молекулы по правой грани куба. Пусть молекула движется со скоростью V₁ вдоль оси X. При упругом ударе о грань она отталкивается с такой же по модулю скоростью, но с обратным знаком. Импульс молекулы до удара (m₀v₁) , а после удара равен (-m₀v₁) . Изменение импульса молекулы за один удар о грань равно (2m₀v₁) . Подсчитаем число ударов, сделанных молекулой о грань за единицу времени (t = 1 с). От удара до следующего удара об одну и ту же грань молекула пролетает вдоль оси Х расстояние, равное удвоенной длине ребра куба 2l, т.к. ей надо пролететь до противоположной грани и вернуться обратно. За одну секунду молекула произведет (v₁/2) ударов. Изменение импульса молекулы за все удары (за 1 сек) можно найти как . Импульс силы f₁t₁, полученный молекулой от грани за все удары в течение секунды, равен изменению ее импульса, т.е. . Такой же импульс получила грань от ударов молекулы. Обозначим число молекул, движущихся вдоль оси Х, через . Аналогично, различные молекулы, двигаясь с другими скоростями сообщают грани импульсы

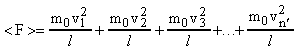или . (8)

Умножим и разделим правую часть равенства (8) на n'. Тогда получим:

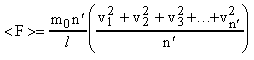. (9)

Сумма квадратов скоростей движущихся молекул деленная на их число равна квадрату средней квадратичной скорости движения молекул, т.е.: (10)

Используя выражение (10), формулу (9) запишем в виде: или, учитывая, что (11)

Давление газа р определяется силой, действующей на единицу площади (площадь грани куба с ребром l равна l2).

или, используя формулу (11) запишем: 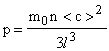. Объем куба V = l³. Такой же объем занимает газ. Поэтому: (12)

Формула (12) есть основное уравнение молекулярно-кинетической теории идеального газа для давления. Сделанный вывод для сосуда в форме куба оказывается справедливым для сосуда любой формы.

Уравнение (12) можно записать иначе. Отношение (число молекул в единице объема или концентрация молекул). Умножим и разделим правую часть равенства (12) на 2. Тогда получим:

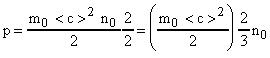
Величина - есть средняя кинетическая энергия поступательного движения одной газовой молекулы. Окончательно имеем: . (13)

Учитывая, что , получим: или . (14)

Таким образом, формулы (12), (13), (14) выражают основное уравнение молекулярно-кинетической теории идеального газа для давления.

Уравнение Клапейрона-Менделеева имеет вид:

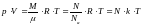
Т. е. из уравнения Клапейрона – Менделеева получили основное уравнения молекулярно-кинетической теории идеального газа.

26.Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры.

Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением

Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с E_k дается соотношением

Это соотношение позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана

k = 1,38·10^–23 Дж/K, которая фактически является переводным коэффициентом, определяющим, какая часть джоуля содержится в градусе.

Согласно последней формуле можно сделать вывод, что температура является мерой средней кинетической энергии поступательного движения молекулы.

27.Число степеней свободы молекул. Внутренняя энергия идеального газа. Закон равнораспределения энергии по степеням свободы.

Важной характеристикой состояния системы является ее внутренняя энергия. Она определяется как среднее значение полной энергии ее частиц. Во внутренней энергии можно выделить следующие составляющие:

- энергия поступательного, вращательного и колебательного движений атомов и молекул;

- энергия межмолекулярного взаимодействия;

- энергия связи атомов в молекулах (химическая энергия);

- энергия связи электронов в атомах;

- энергия связи атомных ядер и др.

Внутренняя энергия системы является функцией ее термодинамических параметров;

Определим внутреннюю энергию идеального газа в равновесном состоянии – это энергия поступательного, вращательного и колебательного движений атомов и молекул. Поступательное движение частиц газа носит классический характер, а вращательное и колебательное движение – квантовый, т.е. такие движения возникают только про сообщении молекулам конечной порции энергии Е.

Закон равнораспределения энергии по степеням свободы.

В состоянии теплового равновесия на каждую поступательную и вращательную степень свободы приходится в среднем энергия, равная kТ/2, а на колебательную – kТ, где k = 1,38·10^–23 Дж/K – постоянная Больцмана.

Числом степеней свободы называется минимальное количество координат, однозначно определяющих положение тела (системы) в пространстве, или количество независимых движений, благодаря которым тело обладает энергией. В атомарном газе каждый атом имеет три поступательных степени свободы, в газе с двухатомными молекулами каждая молекула имеет три поступательных и две вращательных степени свободы, в газе с многоатомными молекулами, в общем случае,  три поступательных и три вращательных. Тогда внутренняя энергия газ имеет вид

,

где i – число степеней свободы молекул газа.

Элементы классической статистики.

28.Закон Максвелла для распределения молекул идеального газа по скоростям теплового движения Средние скорости молекул.

В состоянии теплового равновесия как бы не изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул в газе, при Т=cоnst, остается постоянной и равной .

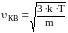Это объясняется тем, что в газе устанавливается некоторое стационарное статистическое распределение молекул по значениям скоростей, называемое распределением Максвелла. Распределение Максвелла описывается некоторой функцией f(), называемой функцией распределения молекул по скоростям.

,

где N – общее число молекул, dN() – число молекул, скорости которых принадлежат интервалу скоростей от  до  + d.

Таким образом, функция Максвелла f() равна вероятности того, что величина скорости наугад выбранной молекулы принадлежит единичному интервалу скоростей вблизи значения . Или она равна доле молекул, скорости которых принадлежат единичному интервалу скоростей вблизи значения .

Явный вид функции f() был получен теоретически Максвеллом:

.

График функции распределения приведен на рис. 12. Из графика следует, что функция распределения стремится к нулю при 0 и  и проходит через максимум при некоторой скорости _В, называемой наиболее вероятной скоростью. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно _В. Значение наиболее вероятной скорости можно найти, используя условие для максимума функции f().

.

На рис. 13 показано смещение _В с изменением температуры, при этом площадь под графиком остается постоянной и равной 1, что следует из условия нормировки функции Максвелла

.

Условие нормировки следует из смысла данного интеграла – он определяет вероятность того, что скорость молекулы попадает в интервал скоростей от 0 до . Это достоверное событие, его вероятность, по определению, принимается равной 1.

Знание функции распределения молекул газа по скоростям позволяет вычислять средние значения любых функций скорости, в частности средней арифметической скорости <>.

.

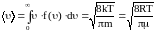Рис.12 Рис. 13

По функции Максвелла можно определить долю молекул, скорости которых принадлежат заданному интервалу скоростей или превышают некоторое значение скорости, например вторую космическую, что определяет рассеяние атмосферы.

.

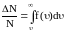29.Газ в потенциальном поле. Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.

Тепловое движение частиц тела приводит к тому, что положение их в пространстве изменяется случайным образом. Поэтому можно ввести функцию распределения частиц по координатам, определяющую вероятность обнаружения частицы в том или ином месте пространства.

где  плотность вероятности, т.е. вероятность обнаружения частицы в единичном объеме вблизи точки с радиус-вектором .

При отсутствии внешних силовых полей существует равномерное распределение частиц идеального газа по координатам, при этом можно записать

,

где n  концентрация частиц, N  полное число частиц газа.

Внешнее силовое поле изменяет пространственное распределение частиц, при этом концентрация частиц и функция распределения зависят от координат. Если внешнее силовое поле является потенциальным, то концентрация частиц вблизи точки пространства с радиусом-вектором зависит от потенциальной энергии частиц в данном месте:

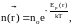
где n_o  концентрация частиц в том месте, где E_p=0.

В этом случае вероятность обнаружить частицу в объеме dV вблизи точки с радиусом-вектором определяется выражением

.

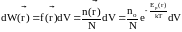Этот закон называется распределением Больцмана.

Для идеального газа давление связано с концентрацией соотношением Р=nkT. В поле земного тяготения концентрация изменяется с высотой над поверхностью Земли, и если газ находится в равновесном состоянии при температуре Т, то изменение давления с высотой происходит по закону

.

П оследнее соотношение называется барометрической формулой. В действительности земная атмосфера не находится в равновесном состоянии, ее температура меняется с высотой, и барометрическую формулу следует применять к участкам атмосферы, в пределах которых изменением температуры можно пренебречь. Из барометрической формулы следует, что давление различных газов изменяется с высотой по-разному. На рис. 14 показано изменение давления газа с высотой для различных газов при T = const, а на рис. 15 – изменение давления газа ( = const) при разных температурах.