Элементы специальной теории относительности.
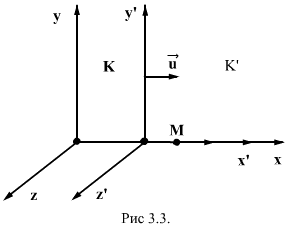
18.Преобразования Галилея. Механический принцип относительности.
Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью u.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K/ будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x',y',z' системы K' так что оси x и x' совпадали, а оси y и y' , z и z', были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x',y',z' той же точки в системе K'. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x'+ut, кроме того, очевидно, что y=y', z=z'. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t'. Получим совокупность четырёх уравнений : x=x'+ut;y=y';z=z';t=t', названных преобразованиями Галилея.
Механический принцип относительности. Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея.
19.Постулаты специальной теории относительности. Преобразования Лоренца.
Первый постулат Эйнштейна: никакими физическими опытами, производимыми внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется прямолинейно и равномерно.
Второй постулат Эйнштейна: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света.
Рассмотрим
две системы отсчета S и S.
Систему S будем считать условно
неподвижной. Система
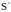движется относительно
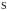со скоростью
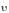вдоль оси X системы
.
Для перехода от одной системы отсчета
в другую в специальной теории
относительности используются
преобразования
Лоренца.
Пусть в начальный момент времени начала координат обеих систем и направления соответствующих осей совпадают. Тогда:
Здесь с = 3108 м/с – скорость света в вакууме.
20.Следствия из преобразований Лоренца. Сокращение продольных размеров движущихся тел.
Рассмотрим две системы отсчета S и S. Систему S будем считать условно неподвижной. Система движется относительно со скоростью вдоль оси X системы .
Изменение размеров движущихся тел
где
L
– длина стержня, расположенного вдоль
оси
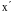и покоящегося в системе S
(отсчитывается в системе отсчета S);
L – длина этого же стержня, измеренная
в системе отсчета
.
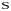21.Следствия из преобразований Лоренца. Замедление хода движущихся часов.
Рассмотрим две системы отсчета S и S. Систему S будем считать условно неподвижной. Система движется относительно со скоростью вдоль оси X системы .
Относительность промежутков времени между событиями:
где
–
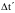промежуток времени между событиями,
произошедшими в системе отсчета
(
отсчитывается
по часам, находящимся в системе
);
– промежуток времени между этими
событиями, отсчитанный по часам,
находящимся в системе
.
22.Релятивистский импульс Основной закон релятивистской динамики материальной точки.
Эйнштейн показал, что масса тела зависит от его скорости:
где m0 – масса тела в той системе отсчета, где тело покоится (масса покоя); m – масса тела в той системе, относительно которой тело движется (релятивистская масса); – скорость тела относительно системы отсчета, в которой определяется масса m, с – скорость света в вакууме.
Релятивистский импульс
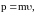
где m – релятивистская масса.
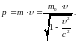
Основной закон релятивистской динамики материальной точки.
,
где
- сила, действующая на материальную
точку.
23.Релятивистское выражение для кинетической энергии. Закон взаимосвязи массы и энергии (формул Эйнштейна)
Закон взаимосвязи массы и энергии:
-
формула
Эйнштейна,
где m – релятивистская масса; Е – полная энергия материального объекта.
Кинетическая энергия объекта
,
где
–
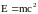полная
энергия;
–
энергия
покоя.
Из закона взаимосвязи массы и энергии следует, что всякое изменение массы тела на m сопровождается изменением его энергии на E:
E=mc2.