
- •Элементы кинематики поступательного и вращательного движения.
- •Динамика поступательного движения.
- •Динамика вращательного движения
- •Элементы специальной теории относительности.
- •Пусть в начальный момент времени начала координат обеих систем и направления соответствующих осей совпадают. Тогда:
- •Основы мкт.
- •Явления переноса. Теплоемкость.
- •30.Среднее число столкновений и средняя длина свободного пробега молекул. Вакуум.
- •Основы термодинамики.
- •Реальные газы.
Динамика вращательного движения
12.Момент силы и момент импульса материальной точки.
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
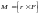 .
.
Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.
Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
 .
.
где r — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, p — импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:

где ri, pi — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
13.Момент импульса и момент силы механической системы относительно неподвижной оси вращения.
Моментом
импульса твердого тела относительно
неподвижной оси Z называется скалярная
величина равная проекции на эту ось
вектора момента импульса, определенного
относительно произвольной точки O данной
оси. Значение момента импульса
![]() не
зависит от положения точки O на оси Z.
не
зависит от положения точки O на оси Z.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
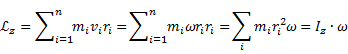
Моментом
силы
![]() относительно неподвижной оси Z называется
скалярная величина равная проекции на
эту ось вектора момента силы
относительно неподвижной оси Z называется
скалярная величина равная проекции на
эту ось вектора момента силы
![]() ,
определённого относительно произвольной
точки O данной оси Z. Если ось Z перпендикулярна
плоскости, в которой лежат векторы
,
определённого относительно произвольной
точки O данной оси Z. Если ось Z перпендикулярна
плоскости, в которой лежат векторы
![]() и
и
![]() ,
т.е. совпадает с направлением вектора
,
то момент силы п
,
т.е. совпадает с направлением вектора
,
то момент силы п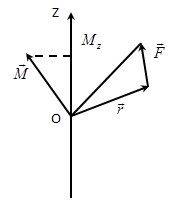 редставляется
в виде вектора совпадающего с осью.
редставляется
в виде вектора совпадающего с осью.
![]()
Ось, положение которой в пространстве остается неизменным при вращении вокруг тела в отсутствие внешних сил, называется свободной осью тела.
Для тела любой формы и с произвольным распределением массы существует 3 взаимно перпендикулярных, проходящих через центр инерции тела оси, которые могут служить свободными осями: они называются главными осями инерции тела.
14.Момент инерции материальной точки и механической системы. Теорема Штейнера.
Инертные
свойства тела при вращательном движении
характеризует момент
инерции.
Он зависит от распределения массы тела
относительно оси вращения. Момент
инерции материальной точки массой m,
находящейся на расстоянии r от оси:
 .
.
 – момент
инерции системы материальных точек;
– момент
инерции системы материальных точек;
 – момент
инерции тела, где
– момент
инерции тела, где
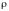 – плотность тела.
– плотность тела.

Момент инерции тела относительно произвольной оси может быть рассчитан по теореме Штейнера: момент инерции тела относительно оси O'O равен сумме момента инерции тела относительно оси, проходящей через центр инерции и параллельной O'O, и произведения массы тела на квадрат расстояния между осями:
 .
.
15.Закон динамики вращения механической системы относительно неподвижной оси.
Скорость изменения момента импульса тела относительно оси равна результирующему моменту внешних сил относительно этой же оси (проекция углового ускорения на ось пропорциональна результирующему моменту внешних сил относительно оси и обратно пропорциональна моменту инерции тела относительно этой же оси):
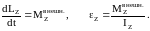 ,
,
Где
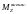 - момент внешних
сил относительно оси z,
- момент внешних
сил относительно оси z,
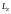 -
момент импульса тела относительно оси
z.
-
момент импульса тела относительно оси
z.
Из законов динамики поступательного и вращательного движений следует условие равновесия тел:
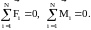
16.Работа при вращательном движении. Кинетическая энергия вращающегося тела.
При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:
 ,
,
если М = const, то А = М.
Кинетическая энергия вращательного движения
,
Где
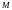 - момент внешних
сил относительно оси вращения,
- момент внешних
сил относительно оси вращения,
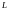 -
момент импульса тела относительно оси
вращения,
-
момент импульса тела относительно оси
вращения,
 - момент инерции тела
относительно оси вращения,
- момент инерции тела
относительно оси вращения,
- угловая скорость тела.
17.Закон сохранения момента импульса и его связь с изотропностью пространства.
Закон сохранения момента импульса: момент импульса замкнутой системы тел сохраняется:

если
 .
.
Если результирующий момент внешних сил не равен нулю, но равна нулю его проекция на некоторую ось, то проекция момента импульса системы на эту ось не изменяется.
В основе закона сохранения момента импульса лежит изотропия пространства, т.е. одинаковость свойств пространства по всем направлениям. Поворот замкнутой системы частиц без изменения их взаимного расположения (конфигурации) и относительных скоростей не изменяет механических свойств системы. Движение частиц друг относительно друга после поворота будет таким же, каким оно было бы, если бы поворот не был осуществлен.
