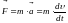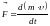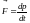Динамика поступательного движения.

4.Представления о свойствах пространства и времени, лежащие в основе классической (ньютоновской) механики. Закон инерции и инерциальные системы отсчёта. Законы динамики поступательного движения инерциальной точки (второй и третий законы Ньютона). Сила как производная импульса.

Считается, что движение тел происходит в пространстве, являющимся евклидовым, абсолютным (не зависит от наблюдателя), однородным (две любые точки пространства неотличимы) и изотропным (два любых направления в пространстве неотличимы).

Время — фундаментальное понятие, постулируемое в классической механике. Считается, что время является абсолютным, однородным и изотропным (уравнения классической механики не зависят от направления течения времени).

Система отсчёта состоит из тела отсчёта (некоего тела, реального или воображаемого, относительно которого рассматривается движение механической системы), прибора для измерения времени и системы координат.

Масса — мера инертности тел.

Материальная точка — модель объекта, имеющего массу, размерами которого в решаемой задаче пренебрегаю

Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Свойство тела сохранять свое состояние называется инертностью. Поэтому первый закон Ньютона называют законом инерции.

Масса тела – физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства.

Сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Основной закон динамики поступательного движения – это второй закон Ньютона, он определяет, как изменяется механическое движение материальной точки или тела под действием приложенных сил.

Второй закон Ньютона: ускорение, приобретаемое материальной точкой или телом, пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

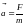
Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно.

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

F12=-F21

Учитывая, что масса в классической механике есть величина постоянная, ее можно внести под знак производной:

Векторная величина , численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки.

Тогда

Это выражение – называется уравнением движения материальной точки – более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.

Единица силы в СИ – ньютон (Н): 1 Н – сила, которая массе 1 кг сообщает ускорение 1 м/с² в направлении действия силы: 1 Н = 1 кгм/с2.

5.Механическая система. Внешние и внутренние силы. Закон динамики поступательного движения механической системы.

Механической системой называется выделенная, каким либо образом совокупность материальных точек.

Тела, не входящие в состав рассматриваемой системы, называют внешними телами, а силы, действующие на систему со стороны этих тел, – внешними силами. Силы взаимодействия между телами внутри системы называют внутренними силами. Результирующая всех внутренних сил, действующих на i-е тело:

где k≠i – т.к. i-я точка не может действовать сама на себя. Обозначим - результирующая всех внешних сил, приложенных к i-ой точке системы. По второму закону Ньютона можно записать систему уравнений:

Сложим эти уравнения и сгруппируем попарно силы и :

По третьему закону Ньютона, , поэтому все выражения в скобках в правой части уравнения равны нулю. Тогда остаётся:

Назовем – главным вектором всех внешних сил, тогда

Скорость изменения импульса системы равна главному вектору всех внешних сил, действующих на эту систему. Это уравнение называют основным уравнением динамики поступательного движения системы тел.

Так как импульс системы , то

Отсюда можно по-другому записать основное уравнение динамики поступательного движения системы тел:

здесь – ускорение центра инерции.

Центр механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе.

6. Центр масс (центр инерции) механической системы и закон его движения.

Центр масс (центр инерции) механической системы - геометрическая точка, характеризующая движение тела или системы частиц как целого.

Закон движения центра масс - произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.

.

Или .

Таким образом, движение центра масс определяется только внешними силами, а внутренние силы никакого влияния на это движение оказать не могут.

7.Замкнутая система. Закон сохранения импульса и его связь с однородностью пространства.

Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют.

Закон сохранения импульса: полный импульс замкнутой системы остается постоянным.

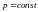
Для замкнутой системы будут сохраняться и проекции импульса на координатные оси:

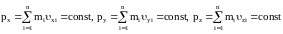
Закон сохранения импульса является отражением фундаментального свойства пространства - его однородности.

8.Работа силы и ее выражение через криволинейный интеграл. Консервативные и неконсервативные силы. Работа консервативных сил.

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.

Элементарной работой силы 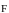называется величина, равная скалярному произведению силы на элементарное перемещение :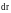

,

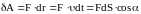где 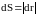– элементарный путь точки приложения силы за время dt,  – угол между векторами и .

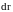Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:

.

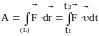Если = const, то А=  .

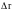Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

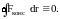
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

9. Кинетическая энергия материальной точки и механической системы и ее связь с работой внешних, внутренних сил, приложенных к системе.

Кинетической энергией тела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).

Кинетическая энергия поступательного движения

.

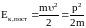Кинетическая энергия вращательного движения

.

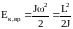При сложном движении твёрдого тела его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:

.

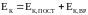Свойства кинетической энергии.

1. Кинетическая энергия является конечной, однозначной, непрерывной функцией механического состояния системы.

2. Кинетическая энергия не отрицательна: Е_К 0.

3. Кинетическая энергия системы тел равна сумме кинетических энергий тел, составляющих систему.

4. Приращение кинетической энергии тела равно работе всех сил, действующих на тело: .

10. Поле как форма материи, осуществляющая взаимодействие между частицами вещества. Потенциальная энергия механической системы. Связь потенциальной энергии материальной точки с силой, действующей на материальную точку (сила как градиент потенциальной энергии).

Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил. Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.

Е_П1 - Е_П2 = Е_П = А_12конс, .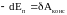

Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.

.

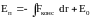Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.

Свойства потенциальной энергии.

1. Потенциальная энергия является конечной, однозначной, непрерывной

функцией механического состояния системы.

2. Численное значение потенциальной энергии зависит от выбора уровня с нулевой потенциальной энергией.

Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии:

,

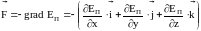причем

, , .

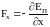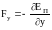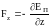Примеры потенциальной энергии:

1) 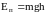– потенциальная энергия тела массой m, поднятого на высоту h относительно нулевого уровня энергии в поле силы тяжести;

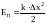2. – потенциальная энергия упругого деформированного тела, х – деформация тела.

11. Полная механическая энергия. Консервативные системы. Закон сохранения механической энергии. Диссипация энергии. Общефизический закон сохранения и превращения энергии.

Полная механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:

Е = Е_к + Е_п.

Консервативная система (от лат. conservo — сохраняю) — физическая система, работа консервативных сил которой равна нулю и для которой имеет место закон сохранения механической энергии, то есть сумма кинетической энергии и потенциальной энергии системы постоянна.

Закон сохранения механической энергии: механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.

Е=const.

Диссипация энергии (лат. dissipatio — рассеяние) — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. п.) в энергию неупорядоченных процессов, в конечном счёте - в теплоту.

В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида.

Общефизический закон сохранения и превращения энергии.

Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии.

Приращение механической энергии системы определяется работой всех неконсервативных сил (внешних и внутренних):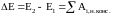 .