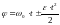Элементы кинематики поступательного и вращательного движения.

1.Система отсчета. Радиус вектор. Путь и перемещение. Скорость и ускорения точки, как производные радиус-вектора по времени.

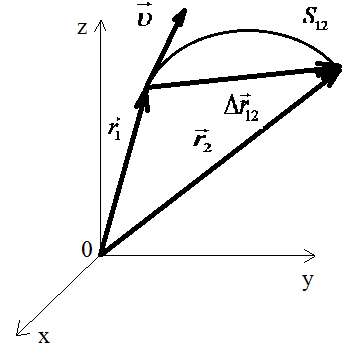
Описать движение материальной точки – значит знать ее положение относительно выбранной системы отсчета в любой момент времени. Системой отсчёта называется система координат, связанная с телом отсчёта и снабжённая синхронизированными часами. Наиболее часто используется прямоугольная декартова система координат (рис. 1).

Положение материальной точки характеризуется радиусом-вектором 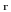, проведённым из начала координат в данную точку.

Движение материальной точки задано, если известна зависимость координат точки от времени, т.е.

или 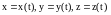.Данные уравнения являются кинематическими уравнениями движения материальной точки, или законом движения точки. В процессе движения конец радиуса-вектора, связанный с точкой, описывает в пространстве кривую, называемую траекторией движения материальной точки. В зависимости от формы траектории различают прямолинейное и криволинейное движения.

Перемещением материальной точки называют вектор, проведённый из начальной точки в конечную точку траектории (рис. 1):

.

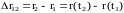Путь материальной точки S₁₂  это длина траектории.

Скорость  векторная физическая величина, характеризующая быстроту изменения положения тела в пространстве, равная перемещению тела за единицу времени. Различают среднюю и мгновенную скорости.

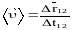 средняя скорость;  мгновенная скорость;

Вектор мгновенной скорости направлен по касательной к траектории движения так же, как вектор элементарного перемещения.

Ускорение  векторная физическая величина, характеризующая быстроту изменения скорости с течением времени, равная приращению скорости за единицу времени. Различают среднее и мгновенное ускорения.

 среднее ускорение,  мгновенное ускорение.

2.Криволинейное движение. Нормальное и тангенциальное ускорения.

Часто используется представление ускорения через две составляющие: тангенциальное и нормальное ускорения.

;

.

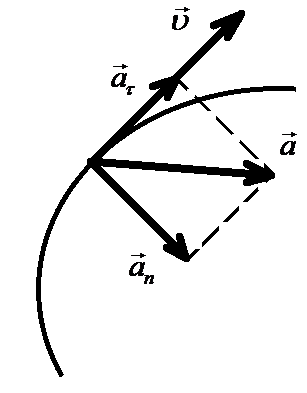
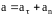Тангенциальное ускорение характеризует изменение скорости по модулю (величине) и направлено по касательной к траектории: ,

где  производная модуля скорости,  единичный вектор касательной, совпадающий по направлению со скоростью.

Нормальное ускорение характеризует изменение скорости по направлению и направлено по радиусу кривизны к центру кривизны траектории в данной точке:

,

где R  радиус кривизны траектории,  единичный вектор нормали.

Модуль вектора ускорения может быть найден по формуле

.

3 .Элементы кинематики вращательного движения. Угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями точек вращающегося тела.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

.

Единица измерения угловой скорости - радиан в секунду (рад/с).

Тогда линейная скорость точки будет равна:

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

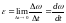, единица измерения углового ускорения - (рад/с²).

Тангенциальная составляющая ускорения

.

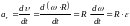Нормальная составляющая ускорения

.

Таким образом, связь между линейными (пути 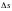- пройденного точкой по дуге окружности радиуса , линейная скорость , тангенциальное ускорение нормальное ускорение ) и угловыми величинами (угол поворота 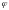, угловая скорость , угловое ускорение ) выражается следующими формулами:

, , , .

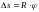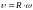В случае равнопеременного движения точки по окружности ( =const)

,
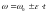