
Упражнение 3
Рассчитаем расчетным путем момент инерции колеса, измерив его размеры.
Момент инерции определяется формулой
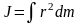 (1).
(1).
Т.к. наше тело сложное, то его можно
разложить на несколько составляющих:
1) «кольцо» - внешний обод, 2) «диск» - само
колесо, 3) «отверстия» в диске, различного
радиуса. (6 отверстий 3-х видов). Тогда
момент инерции будет определяться
формулой
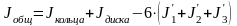 (2), где
(2), где
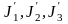 -
моменты инерции «отверстий» относительно
оси вращения,
-
моменты инерции «отверстий» относительно
оси вращения,
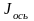 - момент инерции цилиндров, расположенных
на оси вращения.
- момент инерции цилиндров, расположенных
на оси вращения.
Были измерены необходимые параметры исследуемого тела:
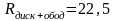 (см),
(см),
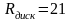 ,1(см),
,1(см),
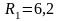 5(см),
5(см),
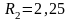 (см),
(см),
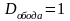 (см),
(см),
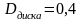 (см),
где R – радиусы, D
– толщина.
(см),
где R – радиусы, D
– толщина.
Для «кольца » имеем формулу объема
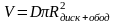 ,
откуда V кольца =
V всего – V
пустоты, V всего = 1492,
25
,
откуда V кольца =
V всего – V
пустоты, V всего = 1492,
25
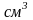 ,
V пустоты = 1293,96
.
V кольца = 198,29
,
по формуле объема
,
V пустоты = 1293,96
.
V кольца = 198,29
,
по формуле объема
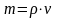 ,
где
,
где
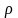 стали = 7,8
стали = 7,8
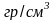 ,
вычислим массу «кольца» m
= 1546,66 гр.
,
вычислим массу «кольца» m
= 1546,66 гр.
Аналогично, для «диска»
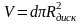 ,
V диска = 388,19
.
Вычисляя по соответствующим формулам
объемы «отверстий», увидим
,
V диска = 388,19
.
Вычисляя по соответствующим формулам
объемы «отверстий», увидим
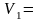 36,21
,
36,21
,
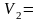 4,56
,
4,56
,
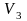 =
0,15
.
Тогда m «диска» =
3027,88 гр., а m1 =
282,44 гр., m2 = 35,57 гр., m3
= 1,17 гр. Используя туже формулу для
вычисления объемов цилиндров, найдем
=
0,15
.
Тогда m «диска» =
3027,88 гр., а m1 =
282,44 гр., m2 = 35,57 гр., m3
= 1,17 гр. Используя туже формулу для
вычисления объемов цилиндров, найдем
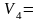 1,08
,
1,08
,
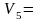 5,54
,
5,54
,
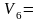 4,71
,
4,71
,
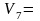 8,59
,
8,59
,
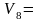 6,28
,
6,28
,
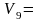 8, 62
.
По формуле
,
где
стали = 7,8
,
8, 62
.
По формуле
,
где
стали = 7,8
,
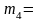 8,42 гр.,
8,42 гр.,
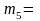 43,21 гр.,
43,21 гр.,
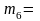 36,74 гр.,
36,74 гр.,
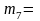 67 гр.,
67 гр.,
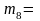 48,98 гр.,
48,98 гр.,
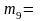 67,24 гр..
67,24 гр..
Исходя из формулы (1), для «кольца»
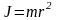 ,
а для «диска», «цилиндров» и «отверстий»
,
а для «диска», «цилиндров» и «отверстий»
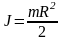 .
.
Следовательно,
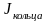 =
735034,70
=
735034,70
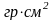 ,
,
 623879,53
,
623879,53
,
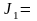 5428,50
,
5428,50
,
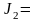 86,08
и
86,08
и
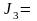 0,09
.
0,09
.
Однако для «отверстий» нам требуется
определить момент инерции относительно
оси вращения тела, для чего мы будем
применять теорему Штейнера
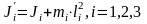 .
Получим
.
Получим
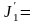 58439
,
58439
,
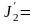 11610
,
11610
,
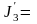 263
.
263
.
Рассчитаем моменты инерции для цилиндров,
их суммой будет
.
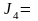 2,06
,
2,06
,
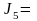 42,35
,
42,35
,
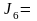 18,37
,
18,37
,
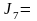 48,24
,
48,24
,
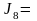 97,96
,
97,96
,
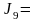 65,90
.
Тогда
=
274,88
.
65,90
.
Тогда
=
274,88
.
Теперь, зная все составляющие величины
момента инерции, можем применить формулу
(2). В итоге, получим

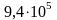 .
.
Вывод
В результате проведенной работы мы научились измерять момент инерции твердого тела (колеса) 2 способами. Схожесть результатов этих экспериментов с теоретически рассчитанным значением доказывает правильность проведения работы.
