Международный университет природы, общества и человека «Дубна»

Институт системного анализа и управления

Кафедра общей физики

Лабораторная работа

студента 2 курса группы 2071

Краснова Михаила Владимировича

по общей физике

на тему:

Измерение момента инерции колеса

Руководитель: Клименко А. А.

Дубна, 2013

Лабораторная работа № 2м

Измерение момента инерции колеса

Цель работы

Познакомиться с методами определения инерции твердого тела (колеса), первый из которых основан на зависимости периода колебаний физического маятника от его момента инерции, второй ­на анализе инерционных свойств твердого тела, закрепленного на оси, при его вращательном движении.

Оборудование

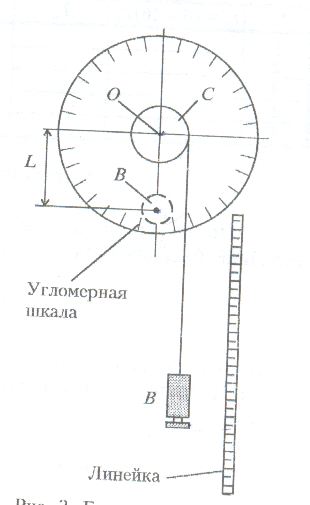
Установка представляет собой ко­лесо (рис. 1), которое может вращать­ся вокруг горизонтальной оси О, про­ходящей через его центр масс. К коле­су на нити, наматываемой на цилиндр С, прикреплен груз В.

Закрепляя (с помощью винта) груз в на колесе на некотором рас­стоянии L от оси вращения, получаем физический маятник. Угол отклонения может быть определен по угломерной шкале.

В случае, когда груз свободно подвешивается на нити, намотанной на цилиндр, под действием силы тяжести он начинает опускаться, приводя коле­со во вращение.

Рис. 1. Блок-схема экспери­ментальной установки

Теоретическая часть

Уравнение вращательного движения твердого тела, закреплен­ного на оси, имеет вид:

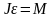, (1)

где J - момент инерции твердого тела, 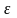- его угловое ускорение, М - момент приложенных к телу сил.

Величина момента инерции относительно какой-либо оси опреде­ляется пространственным распределением элементарных масс 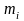тела:

, (2)

где 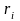- расстояние от элементарной массы до оси вращения.

Для подсчета момента инерции диска с отверстиями нам понадобится Теорема Штейнера, которая звучит следующим образом: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела 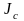  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями.

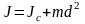, где J_C — известный момент инерции относительно оси, проходящей через центр масс тела, J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями.

Для некоторых тел простой формы возможен прямой расчет момента инерции. При сложной форме поверхности, ограничиваю­щей тело, и неравномерном распределении плотности, аналитиче­ский расчет величины момента инерции может стать непростой зада­чей. В таких случаях можно использовать методы эксперименталь­ного определения моментов инерции.

В данной работе применяются два способа экспериментального определения момента инерции: с помощью анализа коле6аний физи­ческого маятника, составной частью которого является исследуемое тело, и с помощью изучения вращательного движения этого тела.

Рассмотрим эти способы:

Способ 1

Определение момента инерции на основе анализа колебаний физического маятника.

Если закрепить исследуемое тело А на горизонтальной оси, проходящей через центр масс О (рис. 2), то момент сил тяготения равен нулю и тело будет оста­ваться в состоянии безразличного равновесия. Если теперь закре­пить на исследуемом теле на не­котором удалении L от оси малое тело В с известной массой m, то равновесие перестанет быть без­различным - при равновесии дополнительное тело будет распола­гаться под осью на расстоянии L. Такую систему тел можно рас­сматривать как физический маятник.

Уравнение вращательного движения такого маятника в соответствии с (1), имеет вид:

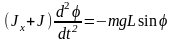, (3)

где 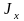- момент инерции твердого тела, J - момент инерции до­полнительного малого тела В относительно оси вращения, g - уско­рение свободного падения, 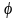- угол отклонения физического маятника от положения равновесия, 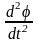- угловое ускорение маятника.

Если углы отклонения малы, то можно написать:

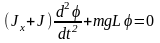. (4)

Рис.2. Схематическое представление физического маятника

Данное уравнение является уравнением колебаний, его решение имеет вид:

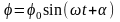, (5)

где 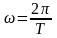- циклическая частота, T – период колебаний, 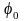- амплитуда колебаний, а 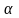- начальная фаза.

Дифференцируя дважды уравнение (5) по времени, получаем

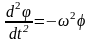. (6)

Сопоставляя (4) и (6), находим

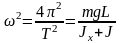. (7)

Учитывая, что размеры тела B во много раз меньше L, можем считать его материальной точкой и положить

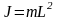. (8)

Тогда из уравнений (7) и (8) получаем

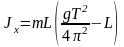. (9)

Таким образом, для определения момента инерции твердого тела можно, закрепив его на оси, проходящей через центр масс, установив на нем добавочное малое тело с известной массой, измерить пе­риод колебаний и, зная расстояние L, по формуле (9) определить неизвестный момент инерции.