127 Определение точки разрыва функции

Точка   называется точкой разрыва функции  , если она определена в некоторой проколотой окрестности точки   (то есть определена на некотором интервале, для которого   служит внутренней точкой, но в самой точке  , возможно, не определена) и выполняется хотя бы одно из следующих условий:

1) не существует предела слева  ;

2) не существует предела справа  ;

3) пределы слева   и справа   существуют, но не равны друг другу:  ;

4) пределы слева   и справа   существуют и равны друг другу:  , но не совпадают со значением функции в точке  :  , или функция   не определена в точке  .

126 Теорема о непрерывности сложной функции

Пусть функция j(t) непрерывна в точке t₀ и функция f(x) непрерывна в точке х₀=j(t₀). Тогда функция f(j(t)) непрерывна в точке t₀.

Доказательство.

Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

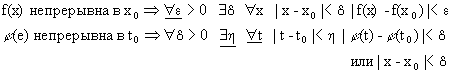
Выписывая подчеркнутые кванторы, получим, что

,

что и говорит о том, что f(j(t)) непрерывна в точке t₀. <

Обратите внимание на следующие детали:

а) т.к. x=j(t), то |j(t)-j(t₀)|<d может быть записано как |x-x₀|<d, и f(x) превращается в F(j(t));

б) при определении непрерывности j(t) в точке t₀ в первом кванторе стоит буква d. Это необходимо для согласования с квантором   в предыдущей строке и взаимного уничтожения  . Любая другая буква на этом месте не дала бы верного результата.

125 Теорема о переходе к пределу под знаком непрерывной функции

Пусть функция   определена в некоторой окрестности точки t0 и имеет  , равный х0. Пусть точка   принадлежит области определения функции y = f(x), и f(x) непрерывна в точке х0. Тогда существует , и  .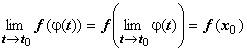

Док-во. Возьмём "e>0. Так как f(x) непрерывна в точке х0, то $s>0, такое что | х- х0|<sÞ Þ | f(x)- f(x0)|<e. Так как существует  = х0, то для s $d>0, такое что 0<| t- t0|<d Þ

Þ |j (t)- х0|<s. Таким образом, для "e>0 мы нашли такое d>0, что из 0<| t- t0|<dÞ

Þ | f(x)- f(x0)|= | f(j (t))- f( )|<e, что означает существование предела  и равенство этого предела величине  .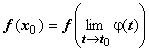

124 Замечательные пределы

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела. Особенно известны:

• Первый замечательный предел:

• Второй замечательный предел:

123 Теорема об устойчивости знака непрерывной в точки функции

Пусть функция   непрерывна в точке   и  . Тогда существует положительное число  такое, что всюду в  –окрестности точки  , функция   имеет тот же знак, что .  Доказательство. Приведем доказательство теоремы для случая Случай   рассматривается аналогично. Т.к., функция  непрерывна в точке  , то для положительного числа  , что для всех  , удовлетворяющих неравенству   будет выполняться неравенство   или  . Из левого неравенства следует, что в каждой точке  , из  –окрестности точки  , справедливо неравенство . Теорема доказана.