144 Теорема о дифференцируемости сложной функции
Если функция u(x) дифференцируема в точке x0, а функция y = f(u) дифференцируема в соответствующей точке u0 = u(x0), тогда сложная функция F(x) = f(u(x)) дифференцируема в точке x0, причем
|
F '(x0) = f '(u0) · u '(x0). |
|
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 101.
В условиях теоремы 1 справедлива формула для дифференциала сложной функции
|
d F(x0) = f '(u0) · u '(x0) dx. |
143 Теорема о непрерывности дифференцируемой функции
Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).
Доказательство
Возьмем
произвольное фиксированное число x 
(a,b).
По условию теоремы
Следовательно,
в малой окрестности числа x0 можно
определить функцию α = α(Δx),
стремящуюся к нулю при 
такую,
что
Но тогда 
и,
следовательно, функция f непрерывна
при x = x0. Так как
число x0 –
произвольное, то функция fнепрерывна
на всем интервале (a, b).
Теорема доказана.
142 Определение дифференцируемой в точке функции
Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке)
141 Определение нормаль
Нормаль — это прямая, ортогональная (перпендикулярная) касательному пространству (касательной прямой к кривой, касательной плоскости к поверхности и т. д.).
140 Определение касательной
Каса́тельная пряма́я в математическом анализе — прямая, проходящая через точку графика функции и имеющая такой же наклон.
Пусть функция
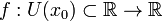определена
в некоторой окрестности точки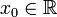 
,
идифференцируема в
ней: 
.
Касательной прямой к графику функции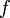 
в
точке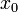 
называется
график линейной
функции, задаваемой уравнением
Если функция имеет в точке бесконечную производную
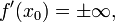то
касательной прямой в этой точке
называется вертикальная прямая,
задаваемая уравнением
139 Геометрический смысл производной
Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
138 Определение производной функции одной переменной
Пусть функция y = f(x) определена в некоторой окрестности точки x0, (включая саму эту точку).
Если существует предел отношения приращения функции Δy = f(x0 + Δx) − f(x0) к вызвавшему его приращению аргумента Δx, когда Δx → 0, то этот предел называется производной функции y = f(x) в точке x0 и обозначается символом f '(x0), т.е.
f '(x0) = lim, гдеΔx → 0 Δy/Δx = lim, где Δx → 0 f(x0 + Δx) − f(x0)/Δx .
137 Определение эквивалентных бесконечно малых
Б.м.
функции 
и 
называются эквивалентными или равносильными
б.м. одного порядка при
,
если 
Обозначают: 
при
.
136 Определение несравнимых функций
.
Если 
не
существует, то α и ß называются несравнимыми
бесконечно малыми.
135 Определение бесконечно малых одного порядка
Если =А 0 (АєR), то α и ß называются бесконечно малыми одного порядка.
134 Определение бесконечно малой более высокого порядка
Если, =0, то α называется бесконечно малой более высокого порядка , чем ß.
133 Вторая теорема Вейерштрасса вторая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения). Доказательство: Пусть f(x)∈C([a;b]) , c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой теореме Вейерштрасса c,d∈R . Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точки x1,x2∈[a;b] , чтоf(x1)=c,f(x2)=d. Докажем, например, существование точки x2.
По определению верхней грани имеем (∀x∈[a;b])(f(x)=d) . Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0 . Далее введем вспомогательную функцию ϕ(x)=1d−f(x) . ϕ(x) на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x) на [a;b]ограничена. Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M) , отсюда имеем f(x)≤d−1M<d . Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, чтоf(x2)=d.
Аналогично доказывается существование точки x1∈[a;b] , такой что f(x1)=c.