
- •168 Теорема о необходимом условии перегиба графика функции.
- •167 Определение точки перегиба графика функции
- •166 Определение выпуклости графика функции вверх
- •165 Определение выпуклости графика функции вниз
- •163 Теорема о необходимом условии экстремуме фоп.
- •162 Определение локального экстремума
- •144 Теорема о дифференцируемости сложной функции
- •143 Теорема о непрерывности дифференцируемой функции
- •142 Определение дифференцируемой в точке функции
- •141 Определение нормаль
- •140 Определение касательной
- •139 Геометрический смысл производной
- •138 Определение производной функции одной переменной
- •132 Первая теорема Вейерштрасса
- •131 Теорема Коши (о промежуточных значениях функции)
- •130 Теорема Больцано-Коши (о нуле функции)
- •129 Определение точек разрыва второго рода
- •128 Определение точек разрыва первого рода
- •127 Определение точки разрыва функции
- •126 Теорема о непрерывности сложной функции
- •125 Теорема о переходе к пределу под знаком непрерывной функции
- •124 Замечательные пределы
- •123 Теорема об устойчивости знака непрерывной в точки функции
173 Определение горизонтальной асимптоты графика функции Пусть функция y=f(x) определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции lim f(x)=b . Тогда прямая y=b есть горизонтальная асимптота графика функции y=f(x) . 172 Определение наклонной асимптоты Пусть функция y=f(x) определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы lim f(x)/x=k и lim (f(x)-kx)=b. Тогда прямая y=kx+b является наклонной асимптотой графика функции y=f(x). Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет. Наклонная асимптота так же, как и горизонтальная, может быть односторонней. 171 Определение вертикальной асимптоты графика функции. Пусть функция y=f(x) определена хотя бы в некоторой полуокрестности точки x=a и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен -~ или +~. Тогда прямая x=a является вертикальной асимптотой графика функции. Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа)
170
Определение
асимптоты графика функции.
Асимптотой
графика функции y=f(x) называется прямая,
обладающая тем свойством, что расстояние
от точки (x,f(x)) графика функции до этой
прямой стремится к нулю при неограниченном
удалении точки графика от начала
координат.
169
Достаточные
условия перегиба графика функции.
1.
Если функция ![]() непрерывна в
точке
непрерывна в
точке ![]() и
имеет в этой точке конечную или бесконечную
производную и если
и
имеет в этой точке конечную или бесконечную
производную и если ![]() меняет
знак при переходе через точку
,
то точка
- точка
перегиба функции
.
меняет
знак при переходе через точку
,
то точка
- точка
перегиба функции
.
Доказательство
Пусть ![]() меняет
знак с «-» на «+», тогда по достаточному
условию строгой выпуклости функция
на
интервале
меняет
знак с «-» на «+», тогда по достаточному
условию строгой выпуклости функция
на
интервале ![]() функция
будет строго выпукла вверх, на интервале
функция
будет строго выпукла вверх, на интервале ![]() —
строго выпукла вниз, т.е при переходе
через точку
направление
выпуклости изменяется
—
строго выпукла вниз, т.е при переходе
через точку
направление
выпуклости изменяется ![]() по
определению
-
точка перегиба.
по
определению
-
точка перегиба.
Вкратце:
первая производная
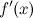 непрерывна
в окрестности точки
непрерывна
в окрестности точки  ;
;вторая производная
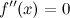 или
не существует в точке
;
или
не существует в точке
; при
переходе через точку
меняет
свой знак,
при
переходе через точку
меняет
свой знак,
тогда
в точке ![]() функция
функция ![]() имеет
перегиб.
имеет
перегиб.
168 Теорема о необходимом условии перегиба графика функции.
Если
точка
— точка
перегиба функции
и
если ![]() в
некоторой окрестности точки
(непрерывная
в точке
),
то
в
некоторой окрестности точки
(непрерывная
в точке
),
то ![]() .
.
Доказательство
Докажем
методом от противного, т.е предположим,
что ![]() .
Тогда
.
Тогда ![]() либо
либо ![]() .
По
условию
непрерывна
в точке
по
свойству сохранения знака непрерывной
функции получим:
.
По
условию
непрерывна
в точке
по
свойству сохранения знака непрерывной
функции получим: ![]() :
: ![]() ,
, ![]() ,
т.е по достаточному условию строгой
выпуклости
,
т.е по достаточному условию строгой
выпуклости ![]()
![]() (функция
выпукла вниз) или
(функция
выпукла вниз) или ![]() (функция
выпукла вверх). Это противоречит
определению точки перегиба, которое
гласит, что при переходе через
точку
направление
выпуклости меняется.
(функция
выпукла вверх). Это противоречит
определению точки перегиба, которое
гласит, что при переходе через
точку
направление
выпуклости меняется.
167 Определение точки перегиба графика функции
Точка
перегиба функции — это точка, в
которой существует касательная к графику
и существует такая окрестность точки ![]() ,
в которой график имеет разные направления
выпуклости. (либо Точкой перегиба графика
функции
называется
точка
,
разделяющая промежутки выпуклости и
вогнутости.)
,
в которой график имеет разные направления
выпуклости. (либо Точкой перегиба графика
функции
называется
точка
,
разделяющая промежутки выпуклости и
вогнутости.)
166 Определение выпуклости графика функции вверх
График функции f(x) называется на интервале ( a, b ) выпуклым вверх если график у=f(x) лежит ниже любой касательной, проведенной к графику в этом интервале.
165 Определение выпуклости графика функции вниз
График функции f(x) называется на интервале ( a, b ) выпуклым вниз если график у=f(x) лежит выше любой касательной, проведенной к графику в этом интервале.
164 Теорема о достаточных условиях экстремума фоп.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки и непрерывна в этой точке. Тогда:
Если производная
 меняет
знак с «-» на «+» при переходе через
точку
:
меняет
знак с «-» на «+» при переходе через
точку
: 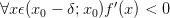 и
и 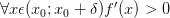 ,
то
—
точка строго минимума функции
,
то
—
точка строго минимума функции 
Если производная меняет знак с «+» на «-» при переходе через точку :
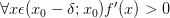 и
и 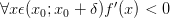 ,
то
—
точка строго максимума функции
,
то
—
точка строго максимума функции
Доказательство
Пусть,
например,
меняет
знак с «-» на «+». Рассмотрим точку
на
сегменте ![]() Воспользуемся
теоремой о конечных приращениях
Лагранжа:
Воспользуемся
теоремой о конечных приращениях
Лагранжа: ![]() ,
, ![]() .
Поскольку при переходе через точку
функция
меняет знак с «-» на «+», то
.
Поскольку при переходе через точку
функция
меняет знак с «-» на «+», то ![]() и
и ![]() ,
то
,
то ![]()
![]() Аналогично
рассмотрим сегмент
Аналогично
рассмотрим сегмент ![]() ,
получим
,
получим
![]()
![]() —
точка строгого минимума функции.
—
точка строгого минимума функции.
Замечания:
Если
—
точка строго экстремума, то из этого не
следует, что производная ![]() меняет
знак при переходе через точку
меняет
знак при переходе через точку ![]()
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть
дана функция
,
ее первая производная ![]() и
пусть
и
пусть ![]() ,
тогда:
,
тогда:
Если , то точка — точка строгого минимума;
Если , то точка — точка строгого максимума.
Доказательство
Докажем
теорему для первого случая, когда
.
Поскольку
непрерывна,
то на достаточно малом интервале ![]() ,
т.к
,
то
,
т.к
,
то ![]() возрастает
в этом интервале.
,
значит
возрастает
в этом интервале.
,
значит ![]() на
интервале
и
на
интервале
и ![]() на
интервале
.
Таким
образом функция
убывает
на интервале
на
интервале
.
Таким
образом функция
убывает
на интервале ![]() и
возрастает на интервале
по
первому достаточному условию экстремума
функция в точке
имеет
минимум.
Аналогично доказывается
второй случай теоремы.
и
возрастает на интервале
по
первому достаточному условию экстремума
функция в точке
имеет
минимум.
Аналогично доказывается
второй случай теоремы.
Замечания:
Если ![]() и
и ![]() ,
то функция
может
и не иметь экстремум в точке
,
то функция
может
и не иметь экстремум в точке
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше 2х)
Пусть ![]() ,
, ![]() и
и ![]() ,
, ![]() Тогда:
Тогда:
Если
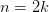 (т.е
(т.е 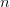 —
четное), то
—
точка экстремума:
—
четное), то
—
точка экстремума:если
 ,
то
—
точка локального максимума;
,
то
—
точка локального максимума;если
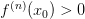 ,
то
—
точка локального минимума;
,
то
—
точка локального минимума;
Если
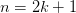 (т.е
—
нечетное), то
—
не является точкой экстремума.
(т.е
—
нечетное), то
—
не является точкой экстремума.
Доказательство
Воспользуемся
формулой Тейлора в окрестности точки
с
остатком в форме Пеано: .
Поскольку
все производные до ![]() порядка
включительно=0 получим:
порядка
включительно=0 получим: ![]() Запишем
полученное выражение в виде: .
Выражение
Запишем
полученное выражение в виде: .
Выражение ![]() .
Пусть
.
Пусть
![]() ,
, ![]() .
.
